Математика играе основна роля в дигиталния свят и особено в видеомонтирането с After Effects (AE), предоставяйки ти изцяло нови възможности. В този урок ще научиш как да използваш тригонометрични и експоненциални функции в AE като изрази, за да създадеш вълнуващи анимации. Един особено интересен пример ще бъде движението на пеперуда, което ще ти покаже как физичните симулации могат да бъдат реализирани с помощта на математика.
Най-важни изводи
- Тригонометрични функции като синус и косинус могат да се използват за създаване на преместени движения.
- Експоненциалните функции се използват за симулиране на ефекти на потискане.
- Използването на абсолютни стойности в функции може да помогне за постигане на определени анимационни ефекти.
Стъпка по стъпка указания
Да накараме пеперудата да се движи
За да накараме нашата пеперуда да се движи, трябва първо да я анимираме така, че да се движи в вълна. Тази вълнова форма може да бъде реализирана без големи усилия чрез изрази.
Започни, като отвориш позицията на пеперудата, натискайки бутона „P“. След това задай израз за позицията, като задържиш ALT и кликнеш върху часовника.
За това първо използваме променливата време time, умножена по стойност, която задава скоростта на движението. Например:
value[0] + time * 150
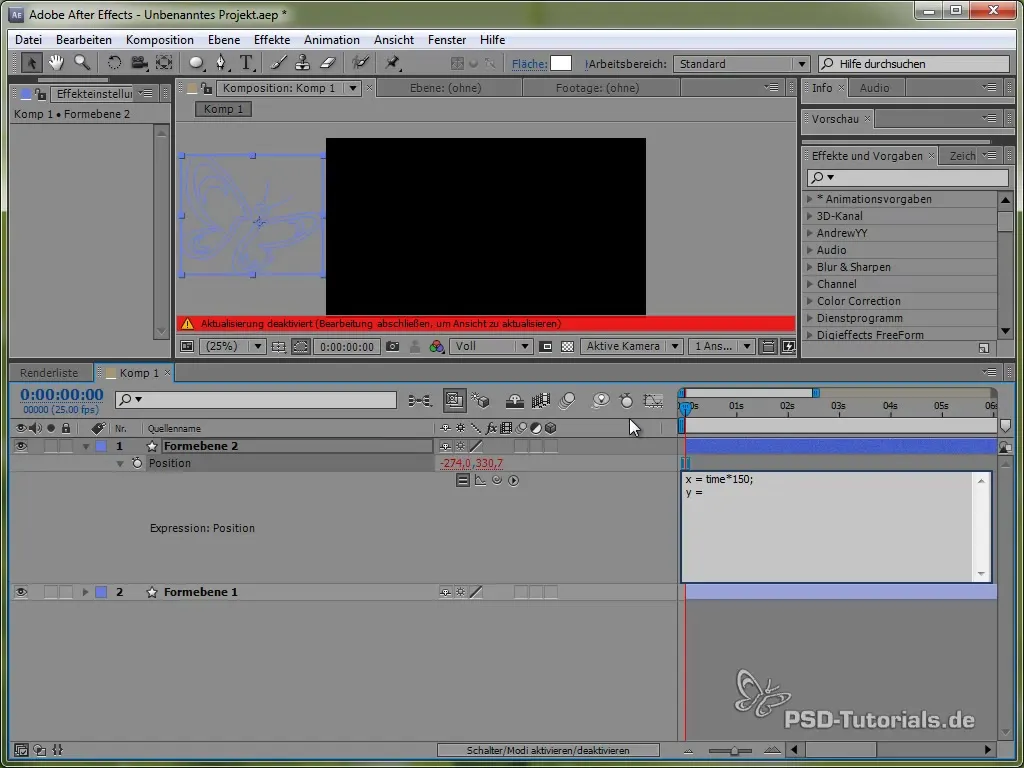
Този код налага пеперудата да се движи в X посока с постоянна скорост от 150 пиксела в секунда. За Y посоката ще използваме синусова функция, която генерира вертикалното движение на пеперудата и я кара да "вибрира" между определени стойности.
Приложение на синусовата функция
Y движението се определя от следния израз:
value[1] + 40 * Math.sin(2 * Math.PI * time)
Като Math.sin() имплементира синусовата функция. Тя варира между -1 и 1 и се умножава по 40, което означава, че пеперудата "вибрира" в Y посока между -40 и 40 пиксела.
Визуализиране на движението
За да визуализираш това движение по-добре, можеш да активираш прозореца за графики в After Effects. Това ще ти покаже колебанията на синусовата стойност по-ясно.
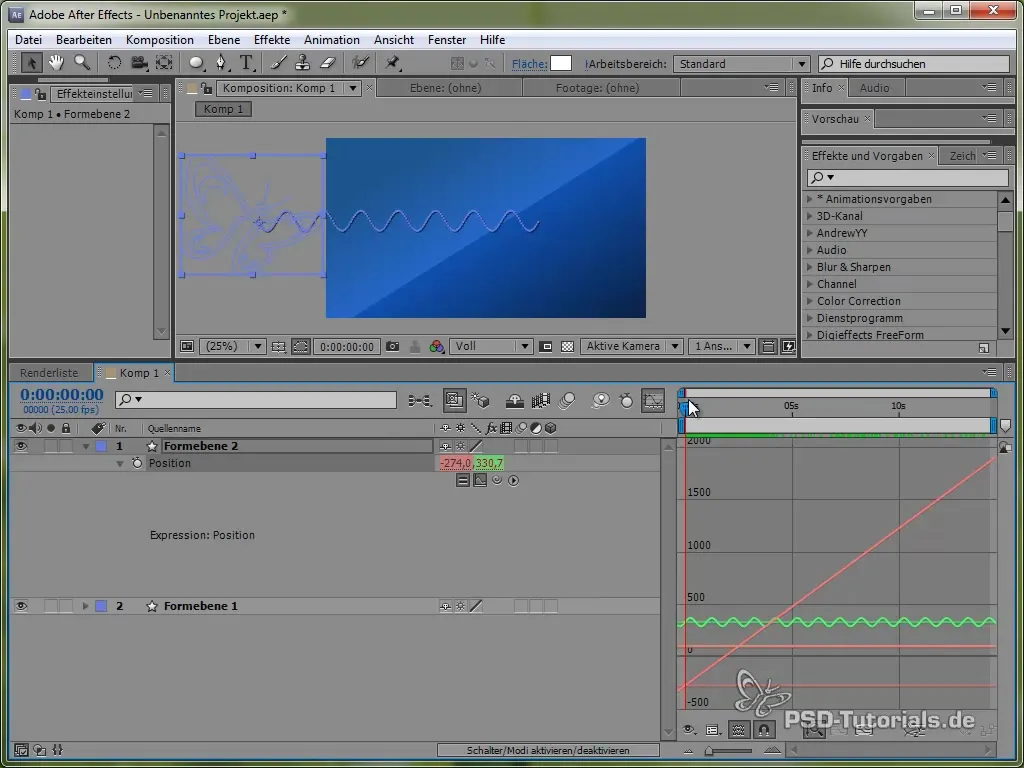
Можеш да видиш, че сигналът осцилира и се движи по екрана.
Вариране на амплитуда и честота
Сега можеш да настроиш амплитудата, за да създадеш различно силни колебания. Например, ако искаш да увеличаваш амплитудата с времето, можеш да използваш следното:
40 * (time * 10) * Math.sin(2 * Math.PI * time)
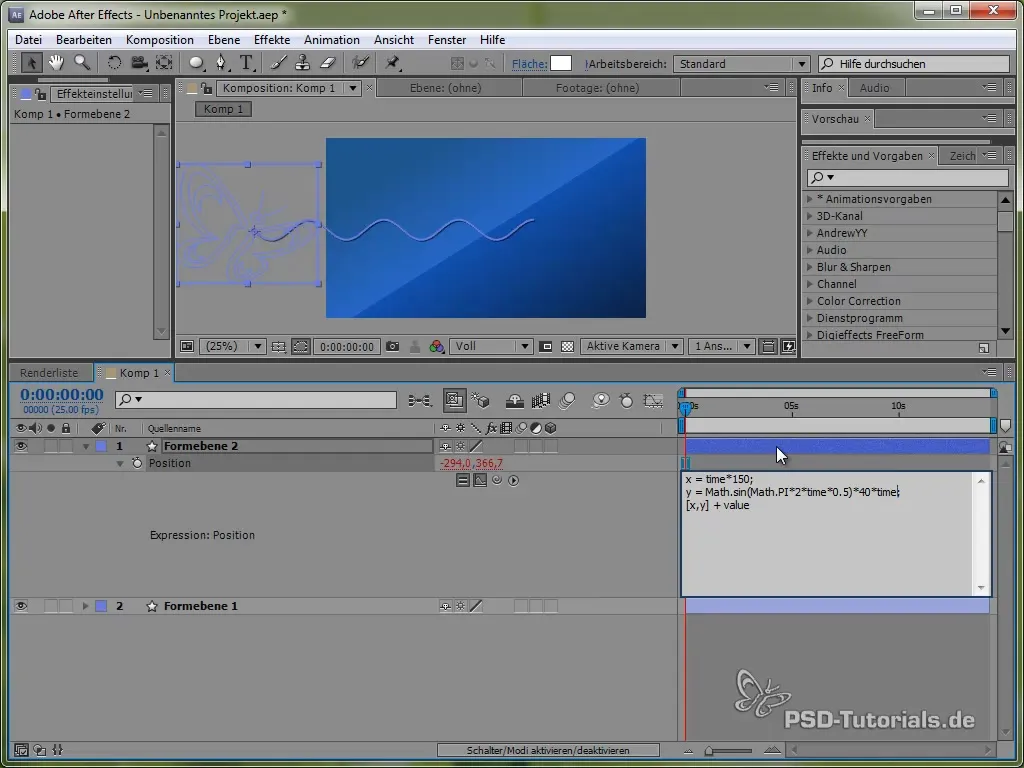
Така амплитудата ще нараства с времето, което ще накара пеперудата да "вибрира" с 40 пиксела след една секунда, с 80 пиксела след две секунди и така нататък.
Създаване на махало
За да задълбочим познанията си за различни физични симулации, сега ще се насочим към създаването на махало. Първо нарисувай тънка пръчка и добави елипса в края й.
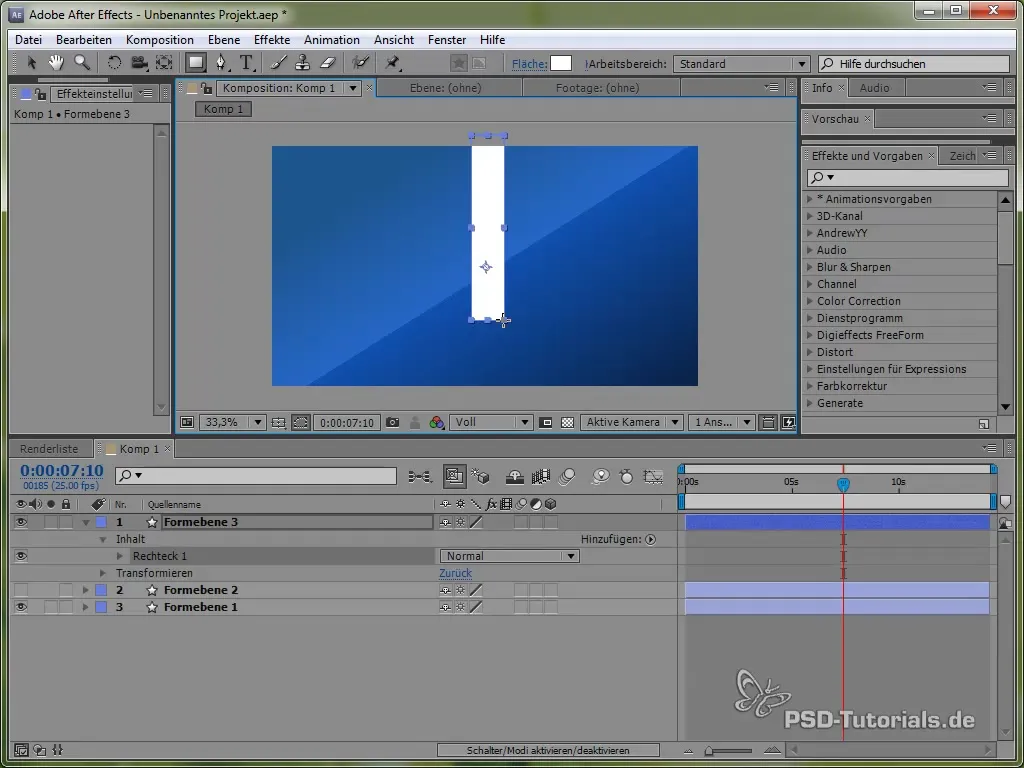
Позиционирай опорната точка в горната част на махалото, така че то да може да се люлее. Това става с инструмента за опорна точка.
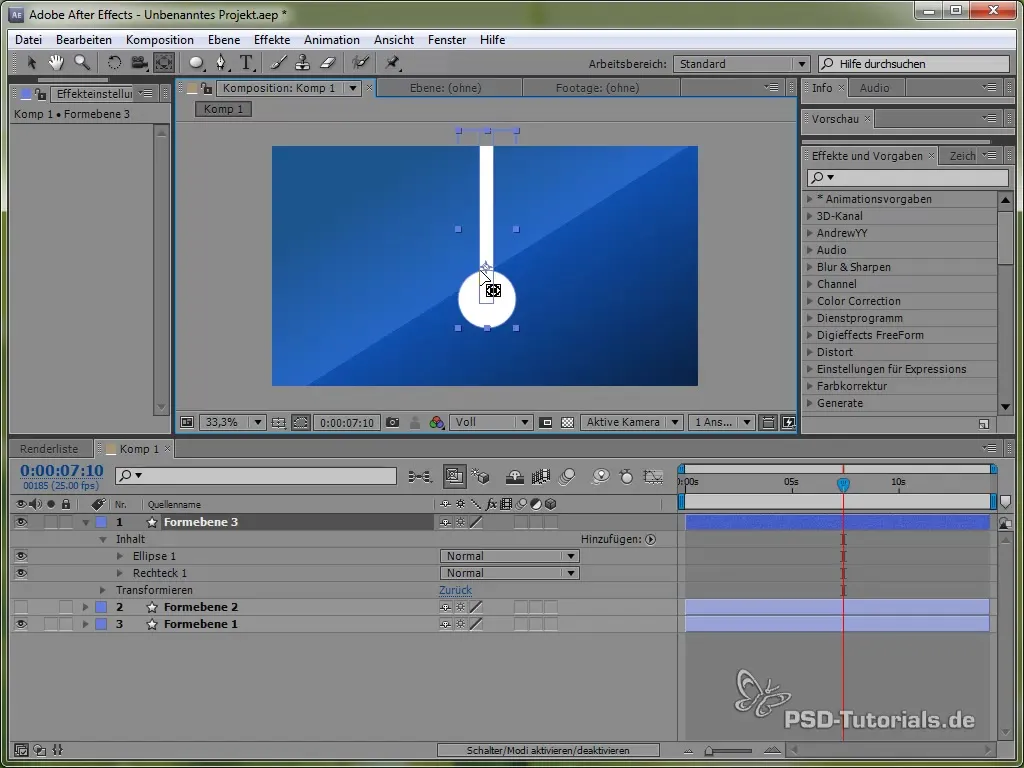
След това задайте израза:
value + 40 * Math.cos(2 * Math.PI * time)
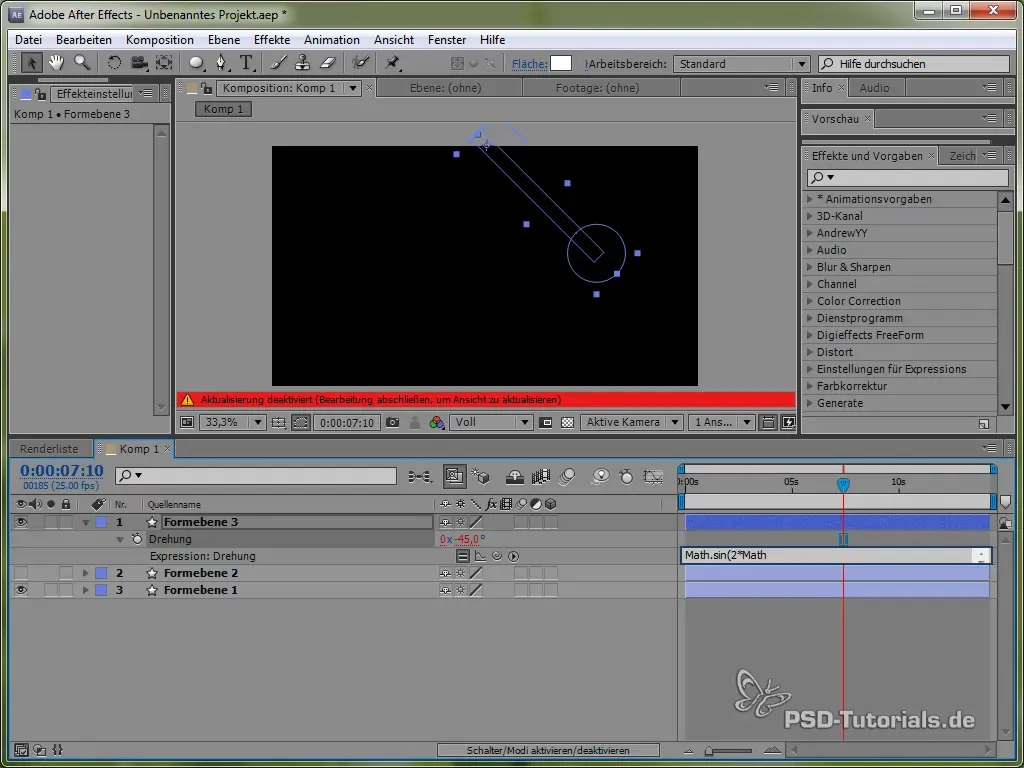
С помощта на косинуса стартираме процеса на колебания от положителна точка, което е реалистично, тъй като махалото започва да се люлее отгоре.
Вмъкване на ефекти на потискане
За да интегрираш потискане в колебанията, използваме експоненциалната функция. Това прави колебанията по-реалистични, защото в началото са силни и след това намаляват.
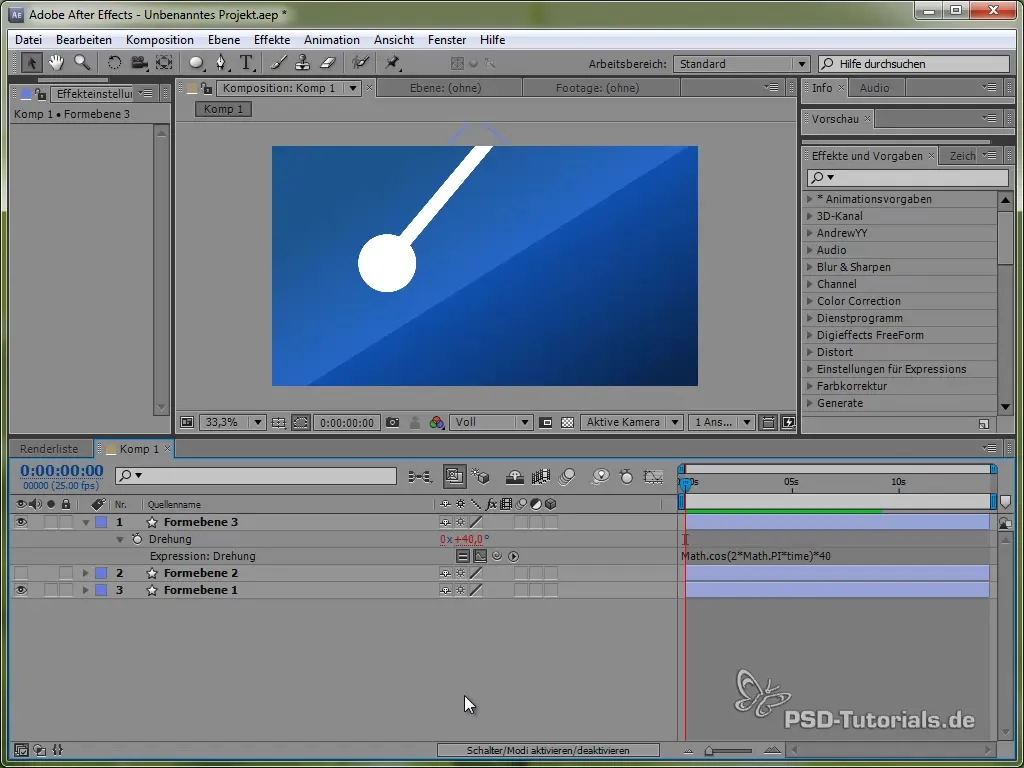
Примерен код може да изглежда така:
40 * Math.cos(2 * Math.PI * time) / Math.exp(time)
Където делението с експоненциалната функция осигурява бавно потискане.
Добавяне на ефект на смачкване и разтягане
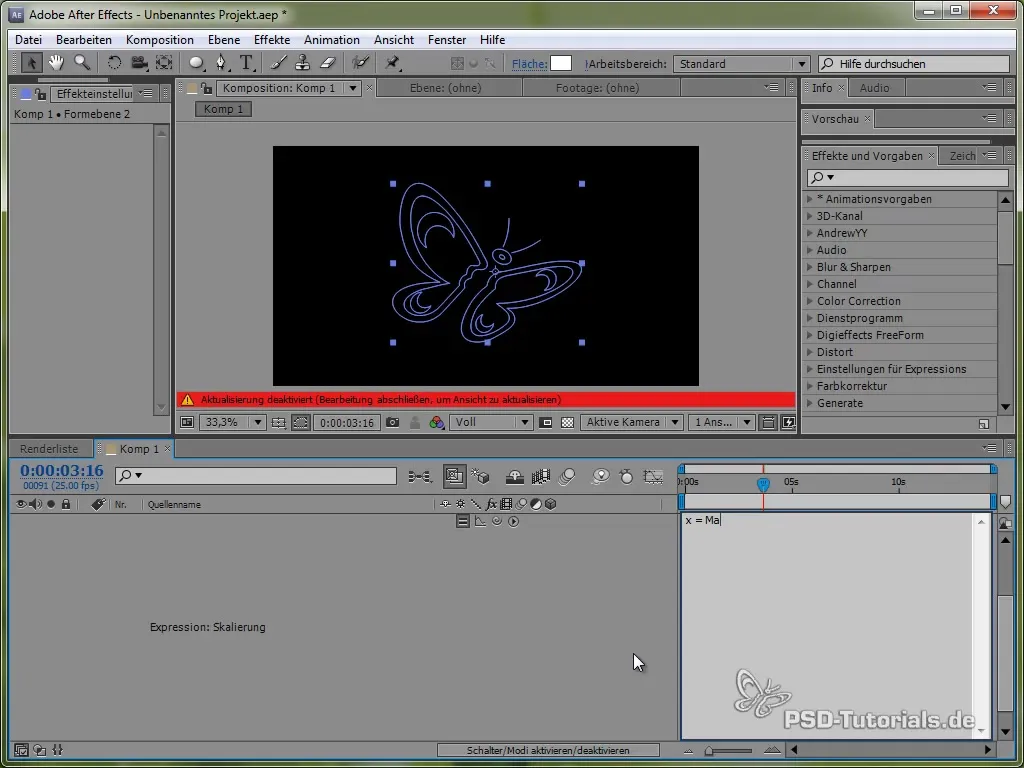
За по-живи анимации можеш да добавиш ефекта на смачкване и разтягане. Това можеш да постигнеш чрез скалиране на пеперудата.
Правиш това, като приложиш израз на скалата за скалиране, който може да бъде приложен както на x, така и на y стойности, използвайки синусова или косинусова функция.
Краен извод
Ясно е, че чрез правилната употреба на тригонометрични и експоненциални функции могат да се създават много реалистични и интересни анимации. Научи как да накараш пеперуда да лети, да люлееш махало и как да работиш с ефекти като смачкване и разтягане.
Обобщение - Математика в изрази: Тригонометрични & Експоненциални функции
Математиката в контекста на изразите в After Effects ти дава възможност да създаваш креативни и живи анимации. Тригонометрични и експоненциални функции са съществени в това. В този урок ти придоби опит в използването на тези математически концепции на практика.
Често задавани въпроси
Как мога да зададна израз в After Effects?Натисни ALT и кликни на часовника до свойството, за което искаш да добавиш израза.
Каква е разликата между синусови и косинусови функции?Синусовата функция започва от 0, докато косинусовата функция започва от 1. Това оказва влияние върху начина, по който стартират анимациите.
Как мога да създам ефекти на потискане?Можеш да генерираш ефекти на потискане, като вмъкнеш експоненциални функции в своите изрази, които намаляват движението с времето.


