Matemáticas juega un papel fundamental en el mundo digital y, sobre todo en la edición de video con After Effects (AE), te abre posibilidades completamente nuevas. En este tutorial aprenderás cómo utilizar funciones trigonométricas y exponenciales en AE como Expresiones para crear animaciones fascinantes. Un ejemplo especialmente emocionante será el movimiento de una mariposa, que te mostrará cómo las simulaciones físicas se pueden implementar con la ayuda de las matemáticas.
Principales conclusiones
- Las funciones trigonométricas como seno y coseno pueden usarse para generar movimientos desfasados.
- Las funciones exponenciales se usan para simular efectos de amortiguamiento.
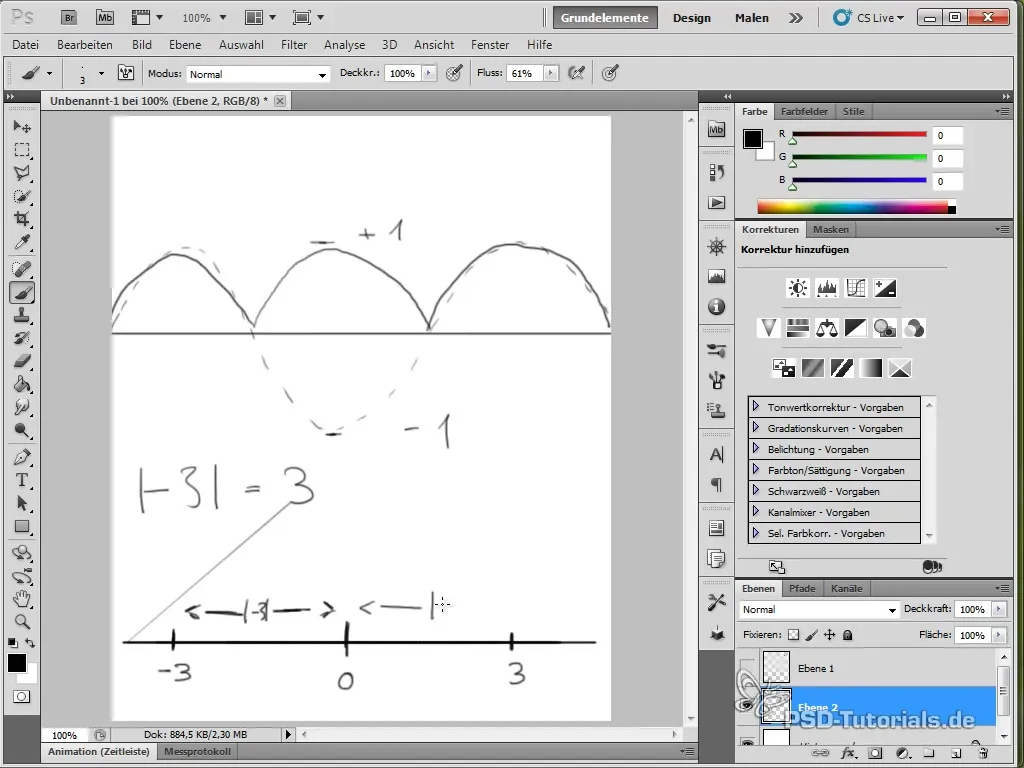
- El uso de valores absolutos en las funciones puede ayudar a lograr ciertos efectos de animación.
Guía paso a paso
Poner en movimiento la mariposa
Para poner en movimiento nuestra mariposa, primero debes animarla de tal manera que se mueva en una ola. Este movimiento ondulante se puede realizar sin mucho esfuerzo a través de expresiones.
Comienza abriendo la posición de la mariposa presionando la tecla "P". Luego, establece una expresión para la posición manteniendo presionada la tecla ALT y haciendo clic en el reloj.
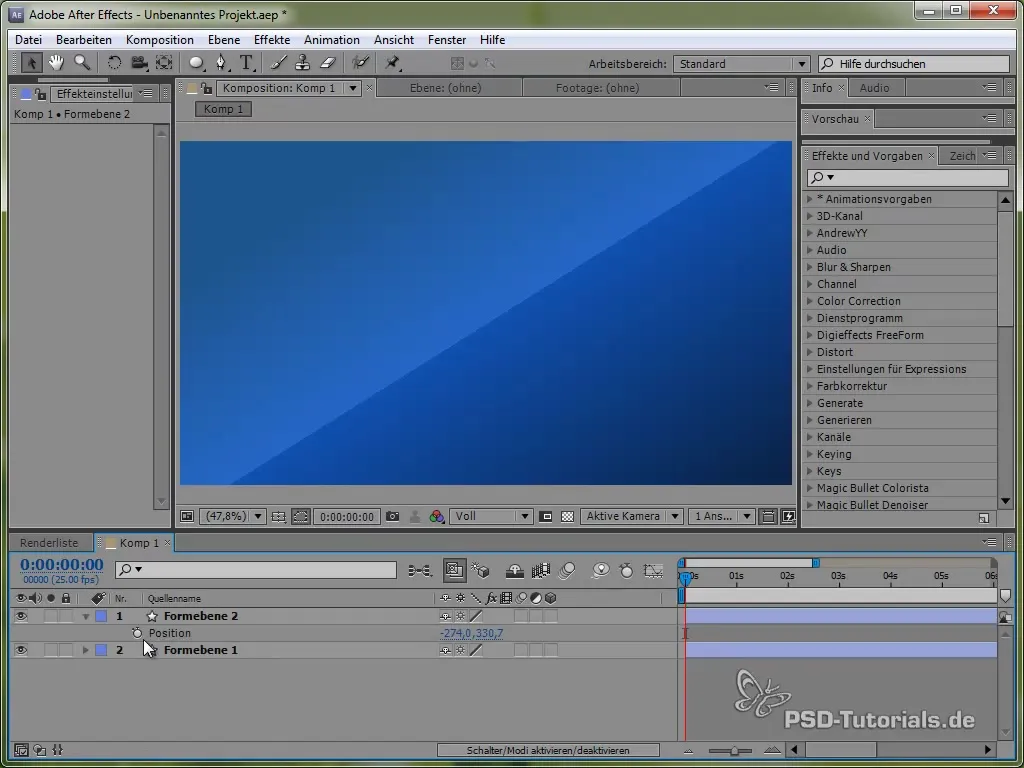
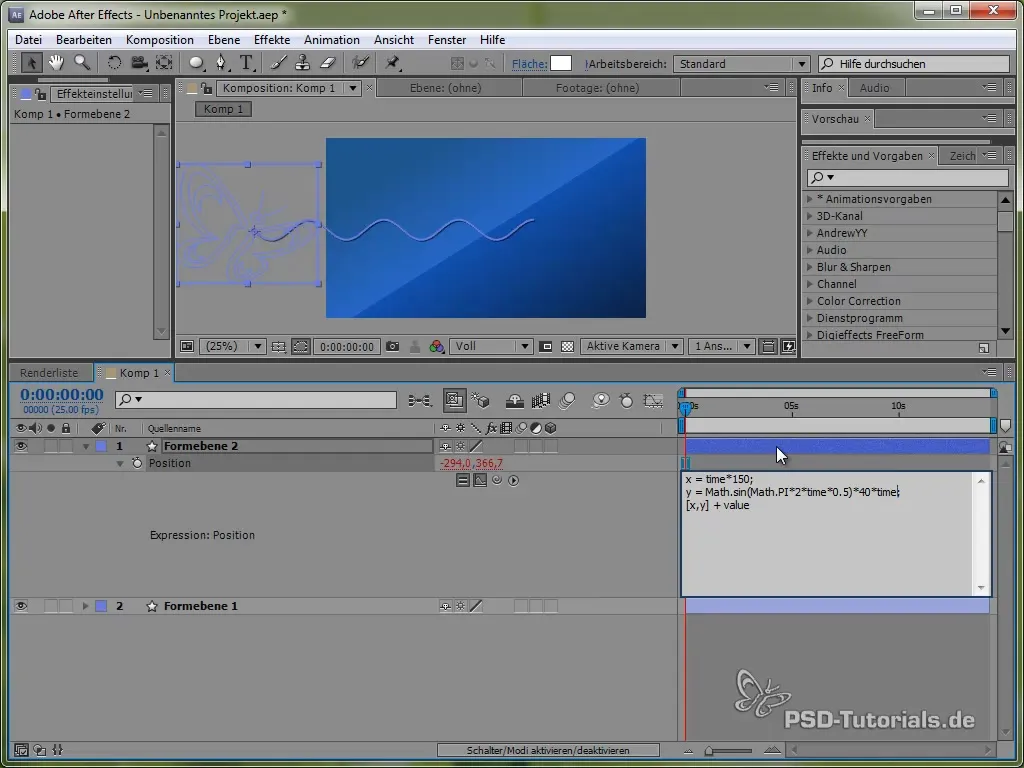
Para esto, primero utilizamos la variable de tiempo time, multiplicada por un valor que establece la velocidad del movimiento. Por ejemplo:
value[0] + time * 150
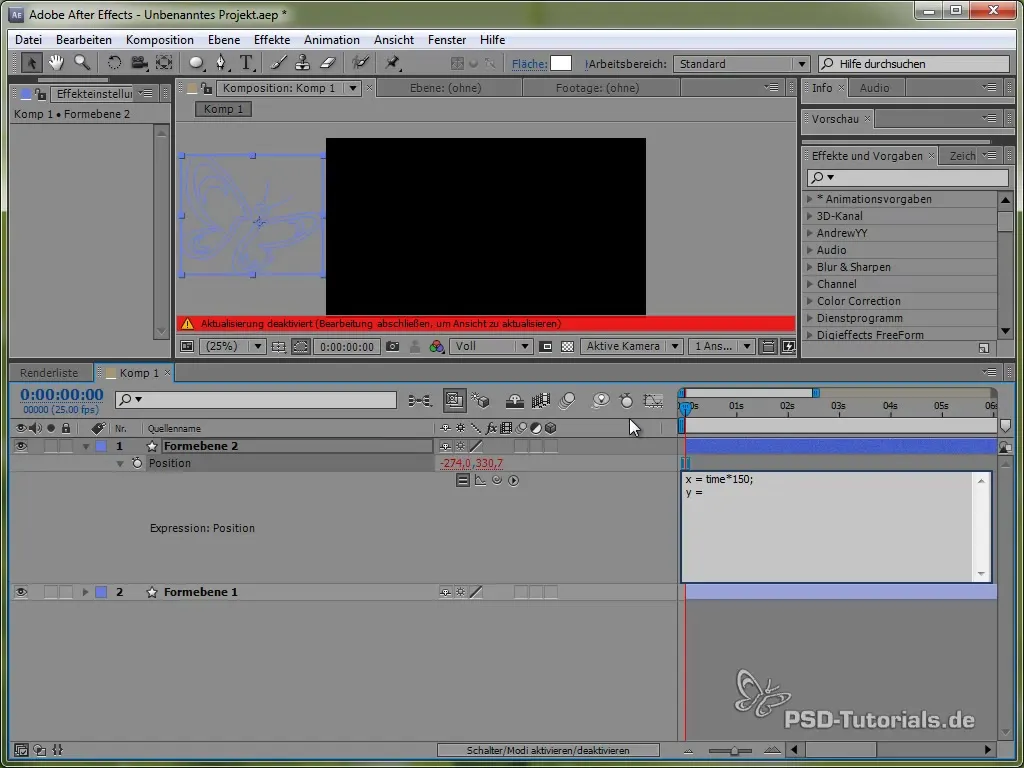
Este código hace que la mariposa se mueva constantemente en la dirección X a 150 píxeles por segundo. Para la dirección Y, utilizaremos una función seno que genera el movimiento vertical de la mariposa y la hace "oscilar" entre ciertos valores.
Aplicación de la función seno
El movimiento en Y se define mediante la siguiente expresión:
value[1] + 40 * Math.sin(2 * Math.PI * time)
Aquí, Math.sin() implementa la función seno. Varía entre -1 y 1 y se multiplica por 40, lo que significa que la mariposa oscila en la dirección Y entre -40 y 40 píxeles.
Visualizar la gráfica de movimiento
Para visualizar mejor este movimiento, puedes activar la ventana de gráficos en After Effects. Esto te mostrará las oscilaciones del valor seno de forma más clara.
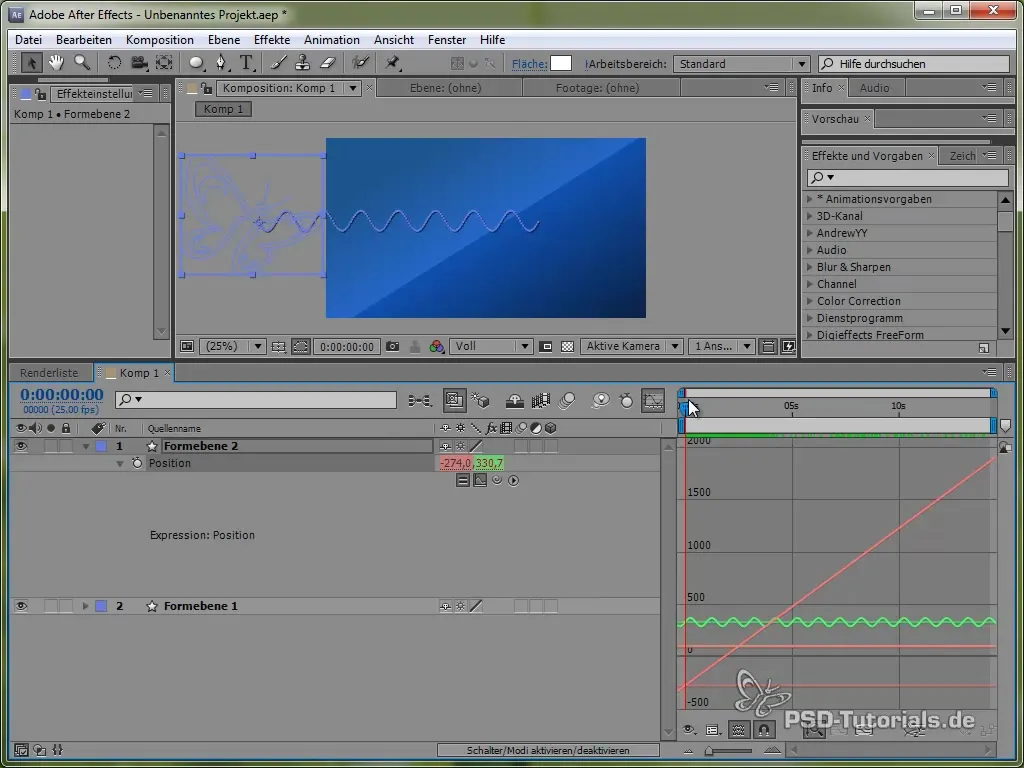
Se puede ver que la señal oscila y se mueve por la pantalla.
Variar amplitud y frecuencia
Ahora puedes ajustar la amplitud para generar oscilaciones de diferente intensidad. Si quisieras, por ejemplo, aumentar la amplitud a lo largo del tiempo, podrías utilizar lo siguiente:
40 * (time * 10) * Math.sin(2 * Math.PI * time)
Esto hará que la amplitud aumente con el tiempo, haciendo que la mariposa oscile 40 píxeles después de un segundo, 80 píxeles después de dos segundos, y así sucesivamente.
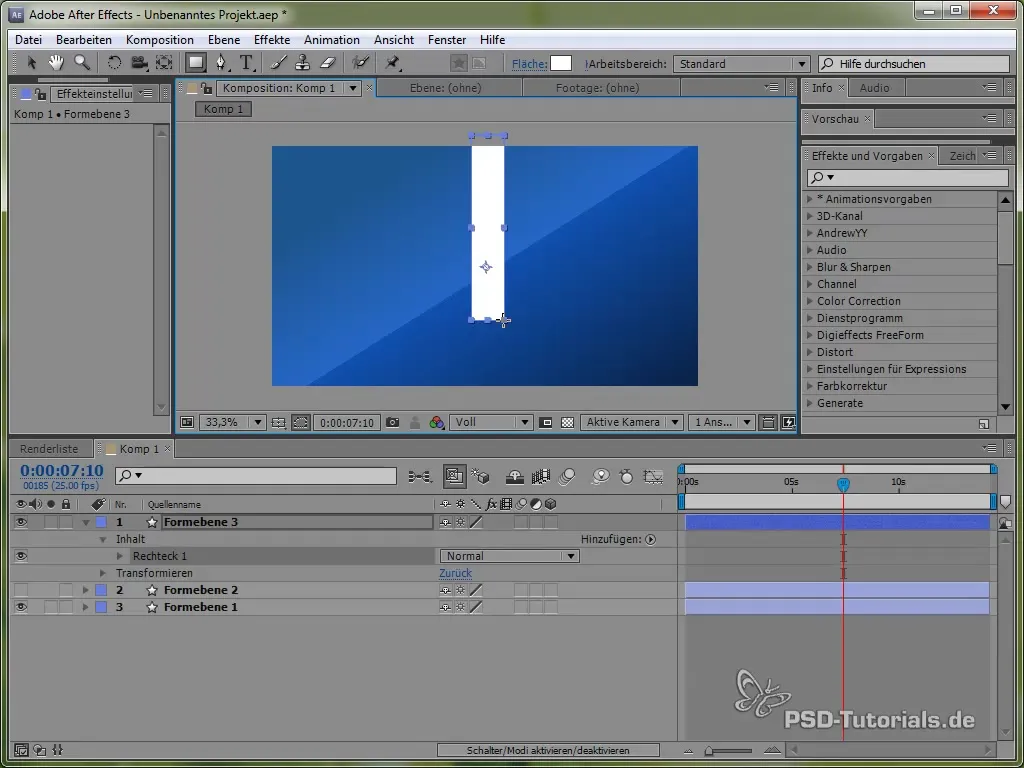
Crear un péndulo
Para profundizar en el manejo de diferentes simulaciones físicas, ahora nos ocuparemos de crear un péndulo. Primero dibuja una barra delgada y agrega una elipse en su extremo.
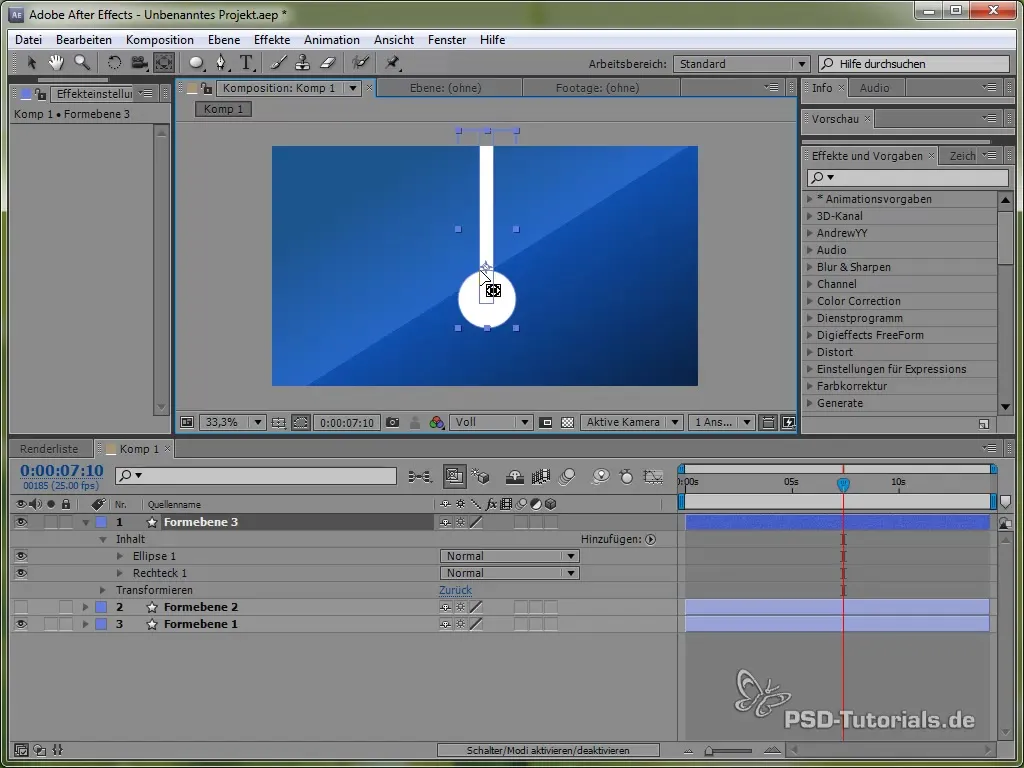
Coloca el punto de anclaje en la parte superior del péndulo para que pueda oscilar. Esto se hace con la herramienta de punto de anclaje.
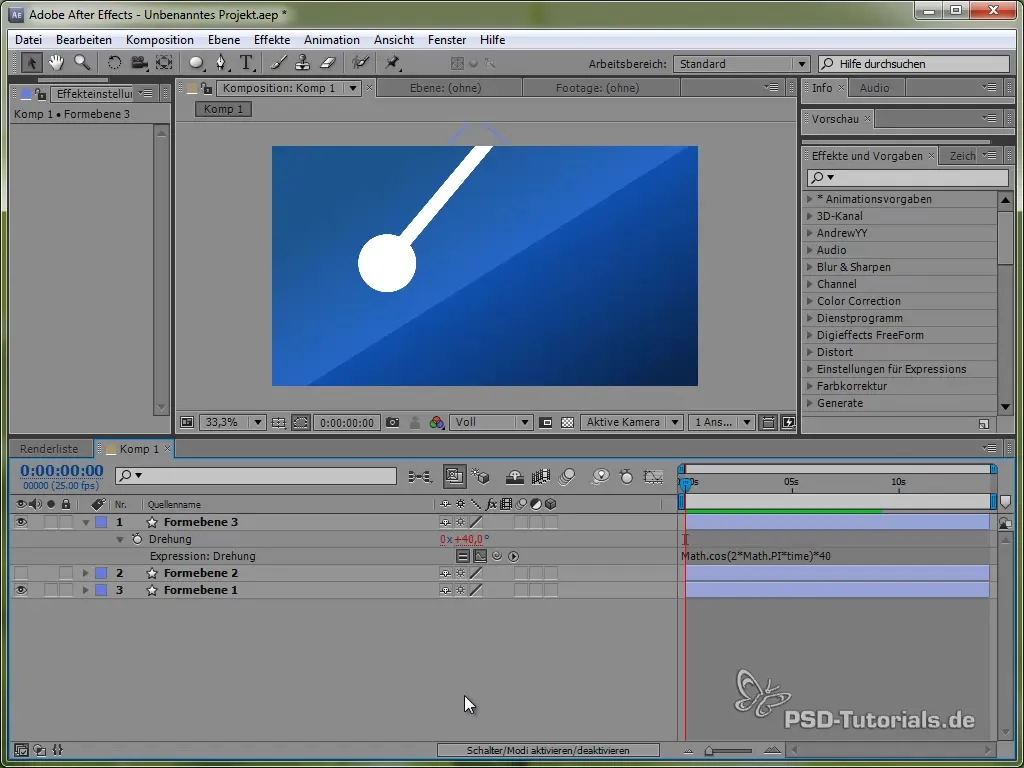
Luego establece la expresión:
value + 40 * Math.cos(2 * Math.PI * time)
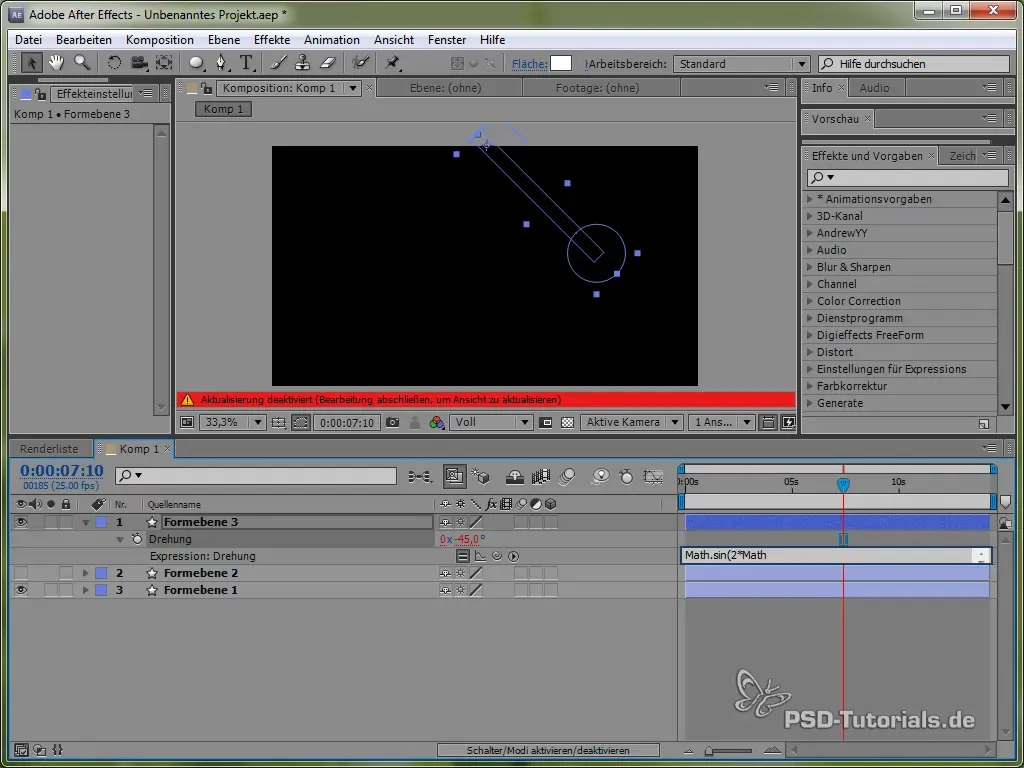
Con el coseno comenzamos el proceso de oscilación desde un punto positivo, lo que es realista, ya que el péndulo comienza a oscilar desde arriba.
Insertar efectos de amortiguamiento
Para integrar el amortiguamiento en la oscilación, utilizamos la función exponencial. Esto hace que la oscilación sea más realista, ya que es fuerte al principio y finalmente disminuye.
Un ejemplo de código podría ser el siguiente:
40 * Math.cos(2 * Math.PI * time) / Math.exp(time)
Aquí, la división por la función exponencial proporciona un amortiguamiento lento.
Agregar squash y stretch
Para animaciones más vivas, también puedes añadir el efecto de squash and stretch. Esto se logra a través de la escala de la mariposa.
Haces esto aplicando una expresión a la escala, que se puede aplicar tanto a valores x como y, utilizando una función seno o coseno.
Pensamientos finales
Se puede ver que mediante la aplicación correcta de funciones trigonométricas y exponenciales se pueden crear animaciones muy realistas e interesantes. Has aprendido cómo hacer que una mariposa vuele, cómo hacer que un péndulo oscile y cómo trabajar con efectos como squash and stretch.
Resumen - Matemáticas en Expresiones: Funciones Trigonométricas y Exponenciales
Las matemáticas en el contexto de las expresiones en After Effects te brindan la oportunidad de crear animaciones creativas y vivas. Las funciones trigonométricas y exponenciales son esenciales. En este tutorial, has adquirido experiencia en el uso de estos conceptos matemáticos en la práctica.
Preguntas frecuentes
¿Cómo aplico una expresión en After Effects?Presiona la tecla ALT y haz clic en el reloj junto a la propiedad a la que deseas agregar la expresión.
¿Cuál es la diferencia entre funciones seno y coseno?La función seno comienza en 0, mientras que la función coseno comienza en 1. Esto afecta cómo comienzan las animaciones.
¿Cómo puedo crear efectos de amortiguamiento?Puedes generar efectos de amortiguamiento incorporando funciones exponenciales en tus expresiones, que reducen el movimiento a lo largo del tiempo.


