Úgy döntöttél, hogy felfedezed a programozás világát a Python segítségével. Minden programozási nyelv elengedhetetlen része a matematikai operátorok, amelyek lehetővé teszik különböző típusú számítások elvégzését. Ebben az útmutatóban nemcsak az alapvető matematikai műveleteket ismerheted meg, hanem a Python 2 és Python 3 közötti különbségeket is tapasztalhatod. Lássunk hozzá, és nézzük meg együtt a különböző számítási módokat.
Legfontosabb megállapítások
- A Pythonban elvégezheted az alapvető matematikai műveleteket, mint az összeadás, kivonás, szorzás és osztás.
- A megjegyzések hasznos módot kínálnak a kód érthetőbbé tételére.
- A egész számok és lebegőpontos számok kezelése eltér a Python 2 és Python 3 között.
- A zárójelek befolyásolják a számítások sorrendjét.
- Hatványokat és gyököket vonhatsz.
- A változók lehetővé teszik a bonyolultabb számításokat, mint például a bruttó összeg meghatározása, beleértve az adókat.
Lépésről lépésre útmutató
1. Alapműveletek a Pythonban
Kezdjük azzal, hogy megnyitsz egy Python környezetet, például a Jupyter Notebook alkalmazást. Itt közvetlenül végrehajthatod a számításaidat.
A kimenetnek 7-et kell mutatnia.
Az eredmény 2 lesz.
2. Szorzás és osztás
A szorzáshoz a Pythonban az a csillag (*) jelet használod.
A kimenet 25. Ha osztani szeretnénk, akkor a per jel (/) segítségével végezzük el.
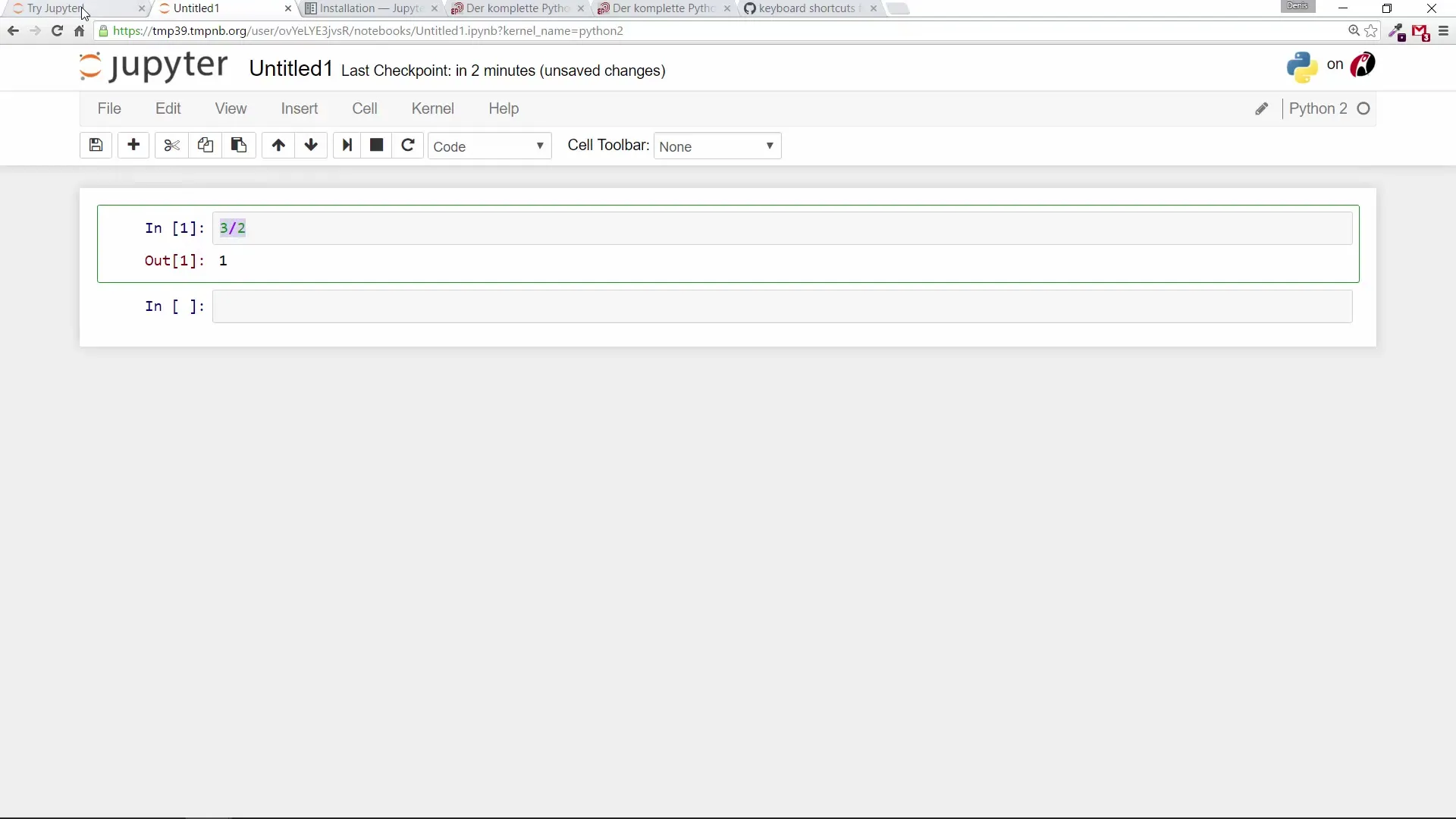
Egy Python 3 környezetben itt 1.5-öt kapsz, míg Python 2-ben csak az 1-es eredményt fogja mutatni.
3. Különbség a Python 2 és Python 3 között
Az egyik legfontosabb különbség, hogy a Python 2 a két egész szám osztásakor csak az eredmény egész részét adja vissza. Ha pontos eredményt szeretnél kapni, biztosítani kell, hogy legalább egy lebegőpontos számot használj.
Ebben az esetben 1.5-öt kapsz eredményül, függetlenül attól, hogy Python 2-t vagy 3-at használsz.
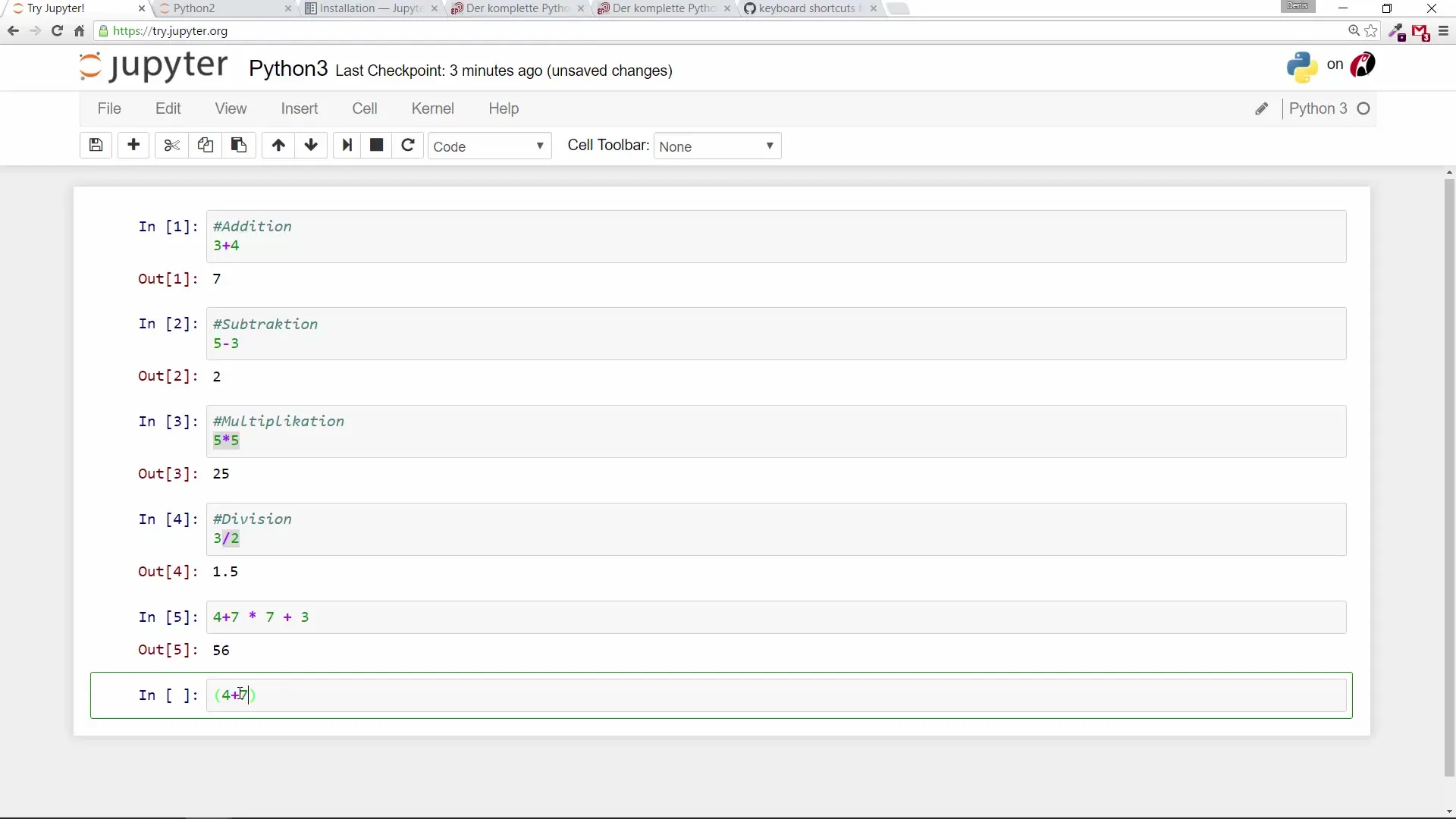
4. A számítások sorrendjének figyelembevétele
A zárójelek használata alapvető fontosságú a számítások sorrendjének befolyásolásához.
A 110-es eredményt ad. Ez megmutatja, mennyire fontos a zárójelek helyes használata.
5. Hatvány és gyökér a Pythonban
A hatványok kiszámításához a dupla csillag (**) jelet használod.
Az eredmény 1024. A gyökereket is kiszámíthatod, ha például 0.5-öt használsz.
Ez adja 4 gyökérértékét, azaz 2.0-t.

6. Változókkal való munka
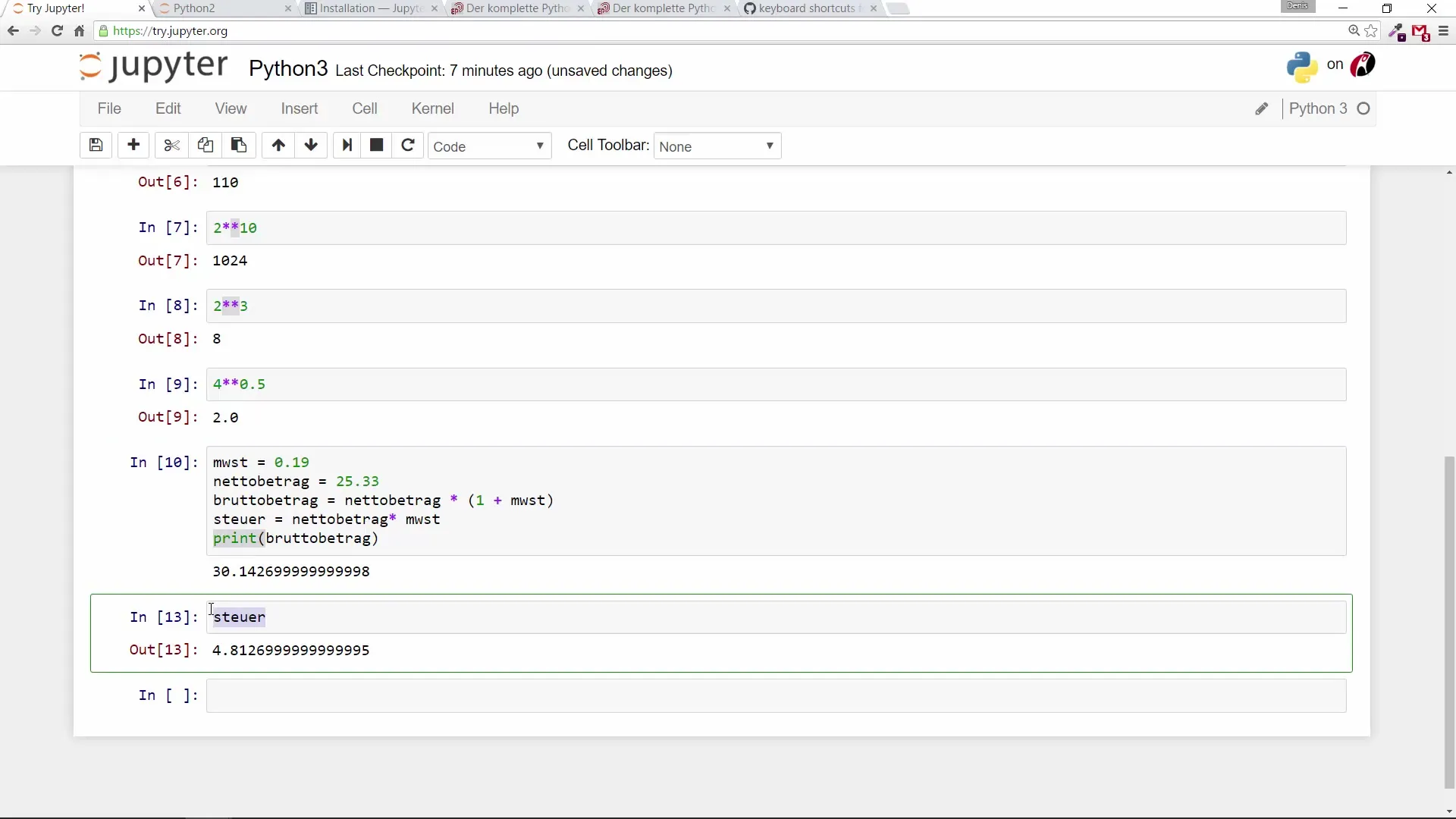
A változók segítségével bonyolultabb számításokat végezhetsz. Tegyük fel, hogy a bruttó összeget szeretnéd kiszámítani, beleértve az áfát.
Ezek a számítások teljes áttekintést adnak a összegekről.
Összefoglalás – Matematikai operátorok a Pythonban
A Pythonban a matematikai operátorokkal egy erőteljes alapot kaptál, ami számos lehetőséget nyújt a számítások elvégzéséhez. Megismerted az alapműveleteket, és észrevetted a Python 2 és Python 3 közötti különbségeket, megértetted a zárójelek jelentőségét a számítások sorrendjében, és használtad a változók koncepcióját a kiterjedt számításokhoz.
Gyakran Ismételt Kérdések
Mik az alapműveletek Pythonban?A Pythonban az alapműveletek az összeadás, kivonás, szorzás és osztás.
Hogyan különböznek a Python 2 és Python 3 az osztás terén?A Python 2 csak az egész számú részt adja vissza, míg a Python 3 pontos eredményt (lebegőpontos szám) ad.
Miért fontosak a zárójelek a számításokban?A zárójelek befolyásolják a számítások sorrendjét, ezáltal megváltoztathatják az eredményt.
Hogyan végezhetek bonyolult számításokat változókkal?A változók értékek tárolására használhatók, így lehetővé teszik azokat matematikai kifejezésekben.
Hogyan számolhatok hatványokat és gyökereket Pythonban?A hatványokat '**'-al számoljuk, a gyökereket pedig az exponenciális formával, például 0.5-tel számolhatjuk.


