A matematika alapvető szerepet játszik a digitális világban, különös figyelmet fordítva a videószerkesztésre az After Effects (AE) programban, ahol teljesen új lehetőségeket kínál. Ebben a bemutatóban megtanulod, hogyan használhatsz trigonometrikus és exponenciális funkciókat az AE-ben kifejezésekként, hogy lenyűgöző animációkat készíthess. Egy különösen izgalmas példa lesz egy pillangó mozgása, amely megmutatja, hogyan lehet fizikai szimulációkat megvalósítani a matematika segítségével.
A legfontosabb megállapítások
- A trigonometrikus funkciók, mint például a szinusz és a koszinusz felhasználhatók eltolódott mozgások létrehozására.
- Az exponenciális funkciók a tompítóhatások szimulálására szolgálnak.
- A függvényekben használt abszolút értékek segíthetnek bizonyos animációs effektusok elérésében.
Útmutató lépésről lépésre
Pillangó mozgása
Annak érdekében, hogy a pillangónkat mozgásba hozzuk, először úgy kell animálnunk, hogy hullámban mozogjon. Ez a hullámmozgás kifejezések segítségével, nagyobb erőfeszítés nélkül megvalósítható.
Kezdd azzal, hogy a pillangó pozícióját a „P” billentyű megnyomásával megnyitod. Ezután állíts be egy kifejezést a pozícióhoz úgy, hogy lenyomod az ALT billentyűt, majd rákattintasz az órára.
Ehhez először a time időváltozót használjuk, megszorozva egy értékkel, amely meghatározza a mozgás sebességét. Például:
value[0] + time * 150
Ez a kód azt eredményezi, hogy a pillangó az X irányban folyamatosan 150 pixel/ másodperc sebességgel mozog. Az Y irányban szinusz funkciót fogunk használni, amely létrehozza a pillangó függőleges mozgását, és a pillangót meghatározott értékek között „ringatja”.
A szinusz funkció alkalmazása
A Y mozgás a következő kifejezéssel van definiálva:
value[1] + 40 * Math.sin(2 * Math.PI * time)
Itt a Math.sin() a szinusz funkciót valósítja meg. Az érték -1 és 1 között változik, és 40-nel van megszorozva, ami azt jelenti, hogy a pillangó az Y irányban -40 és 40 pixel között ingadozik.
A mozgásgrafika vizualizálása
Ennek a mozgásnak a jobb vizualizálásához aktiválhatod a grafikon ablakot az After Effects-ben. Ez világosabban megmutatja a szinusz érték ingadozását.
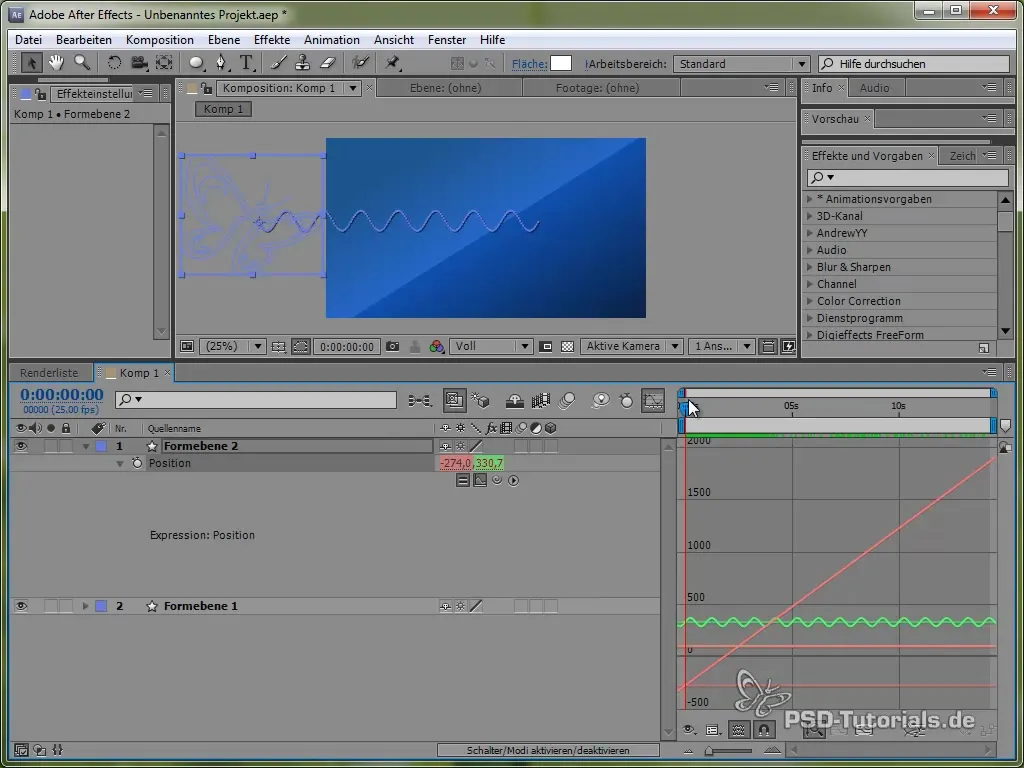
Látható, hogy a jel oszcillál és a képernyőn mozog.
Az amplitúdó és a frekvencia változtatása
Most módosíthatod az amplitúdót, hogy különböző fokú ingadozásokat létrehozz. Például, ha az amplitúdót idővel szeretnéd növelni, ezt használhatod:
40 * (time * 10) * Math.sin(2 * Math.PI * time)
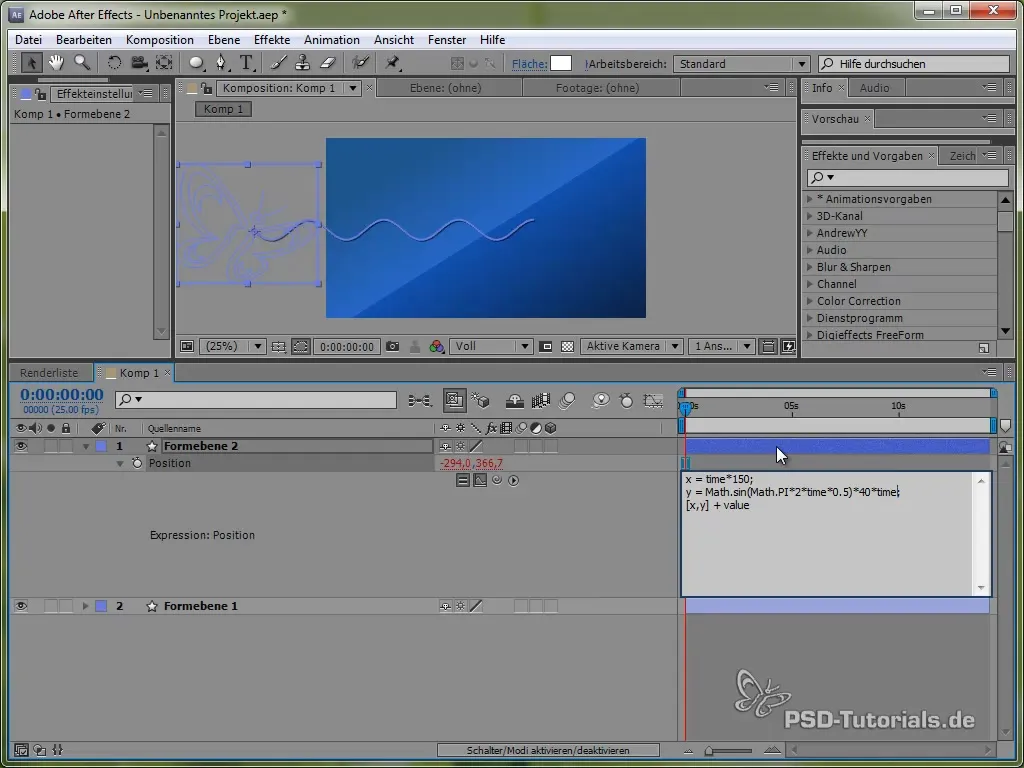
Ez az amplitúdót idővel növelni fogja, így a pillangó egy másodperc után 40 pixel ingadozni fog, két másodperc után 80 pixel, és így tovább.
Libikóka létrehozása
A különböző fizikai szimulációk kezelésének elmélyítése érdekében most áttérünk egy libikóka létrehozására. Először rajzolj egy vékony rudat, és adj hozzá egy ellipszist annak végéhez.
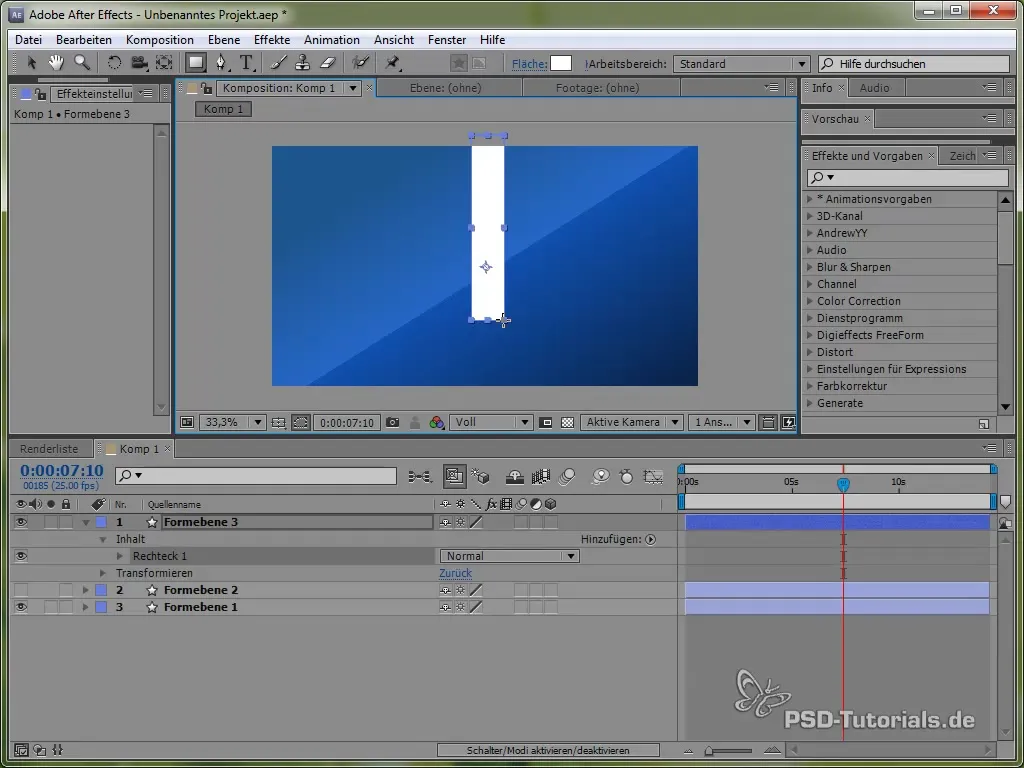
Pozicionáld a rögzítési pontot a libikóka tetejére, így az ingadozhat. Ezt az Ankerpont eszközzel érheted el.
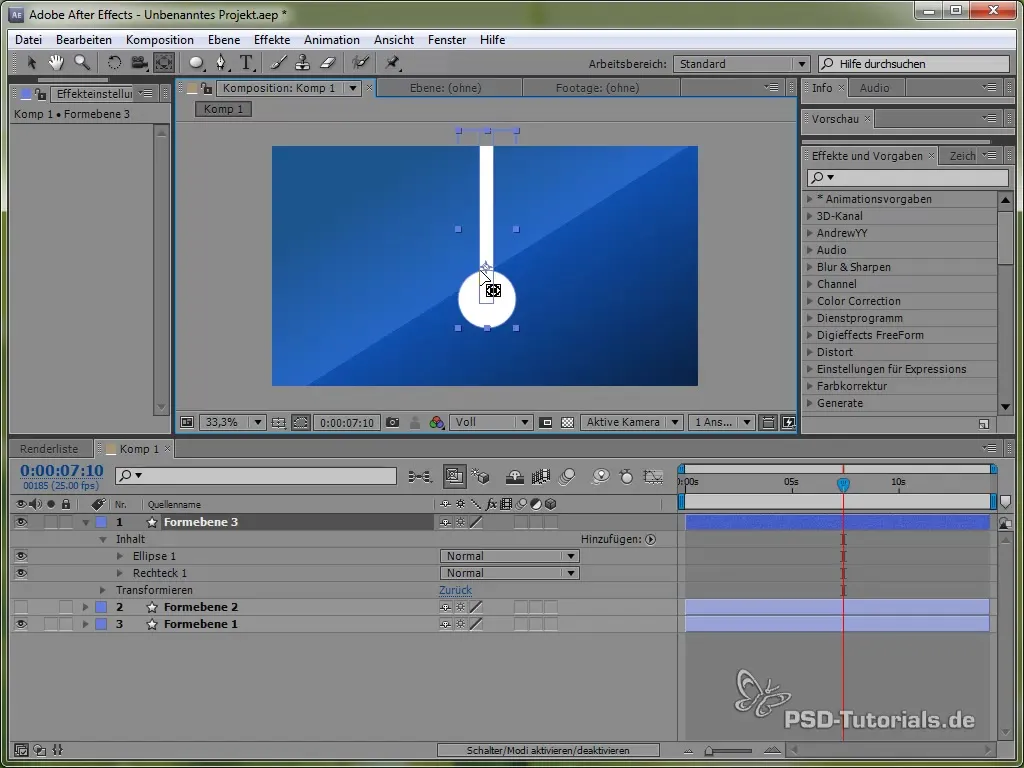
Ezután add meg a következő kifejezést:
value + 40 * Math.cos(2 * Math.PI * time)
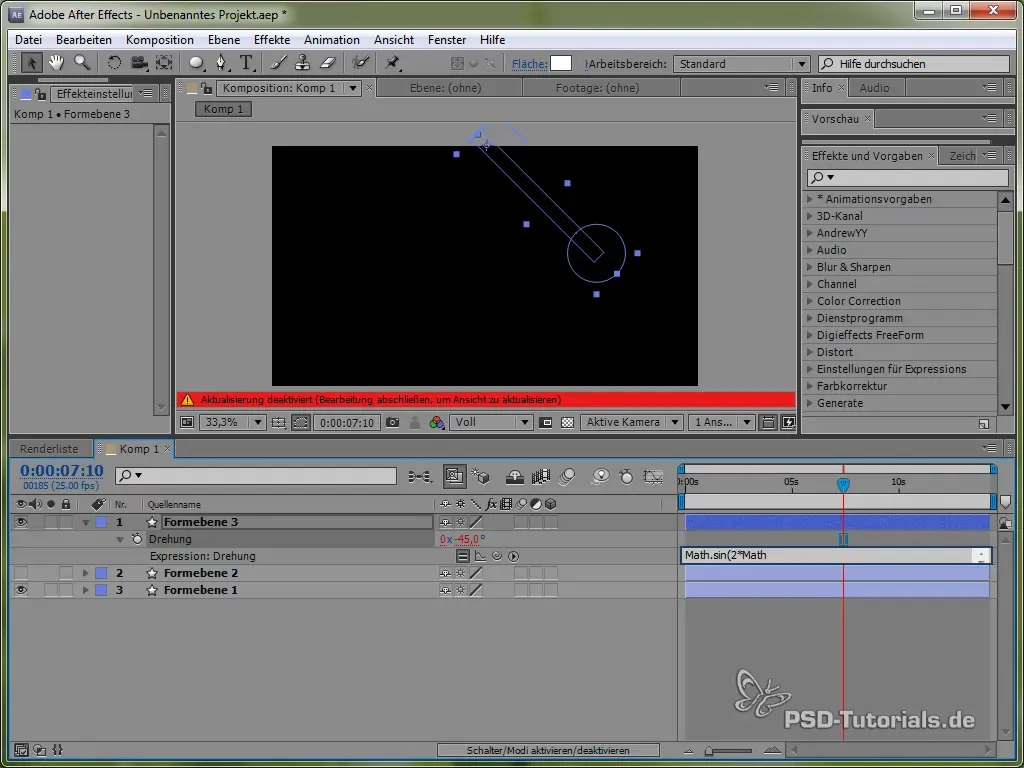
A koszinusszal a mozgássorozatot egy pozitív pontból indítjuk, ami reális, mivel a libikóka fent kezd ingadozni.
Tompító hatások hozzáadása
A tompítás beiktatásához a rezgésbe exponenciális funkciót használunk. Ez által a rezgés valóságosabbá válik, mivel kezdetben erős, majd fokozatosan csökken.
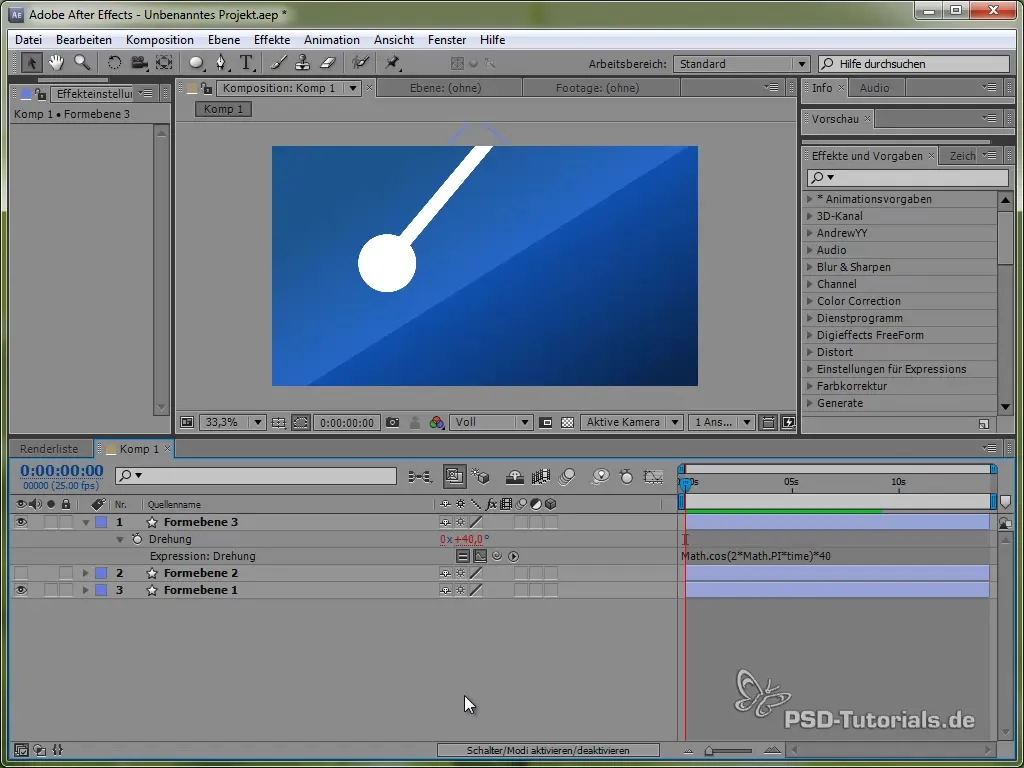
Egy példa kód így nézhet ki:
40 * Math.cos(2 * Math.PI * time) / Math.exp(time)
Itt az exponenciális függvénnyel való osztás lassú tompítást biztosít.
Összenyomás és nyújtás hozzáadása
A színesebb animációk érdekében a Squash and Stretch effektust is hozzáadhatod. Ezt a pillangó skálázásával érheted el.
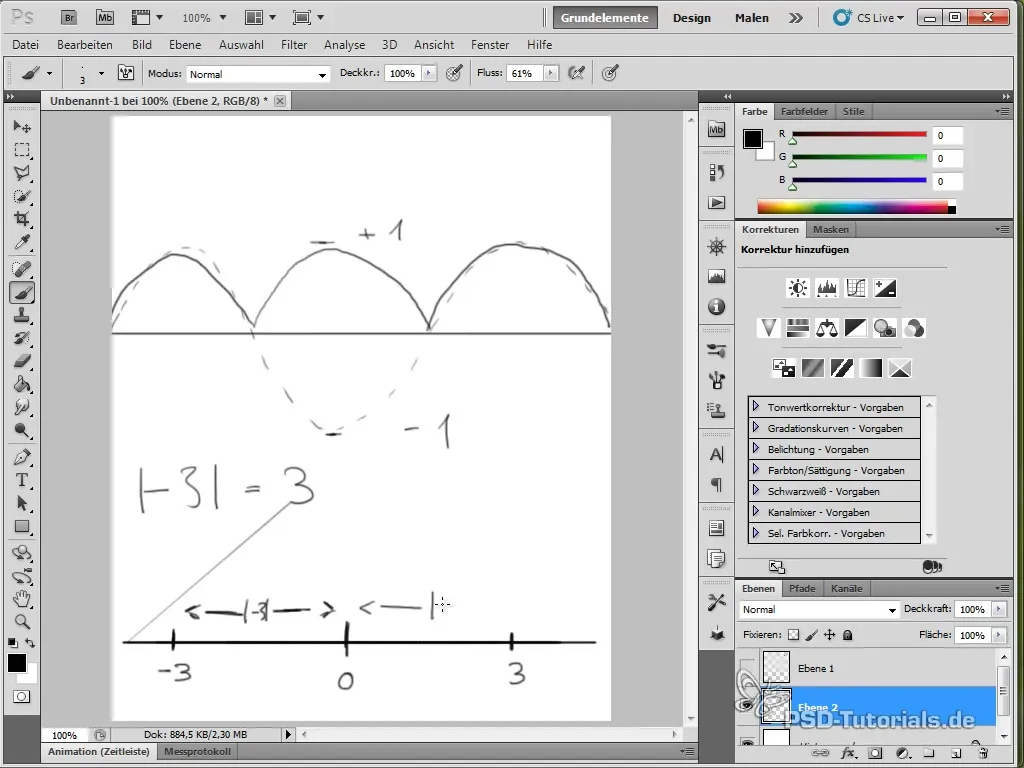
Ezt úgy teszed, hogy kifejezést alkalmazol a méretarányra, amely mind az x, mind az y értékekre alkalmazható, használva egy szinusz vagy koszinusz funkciót.
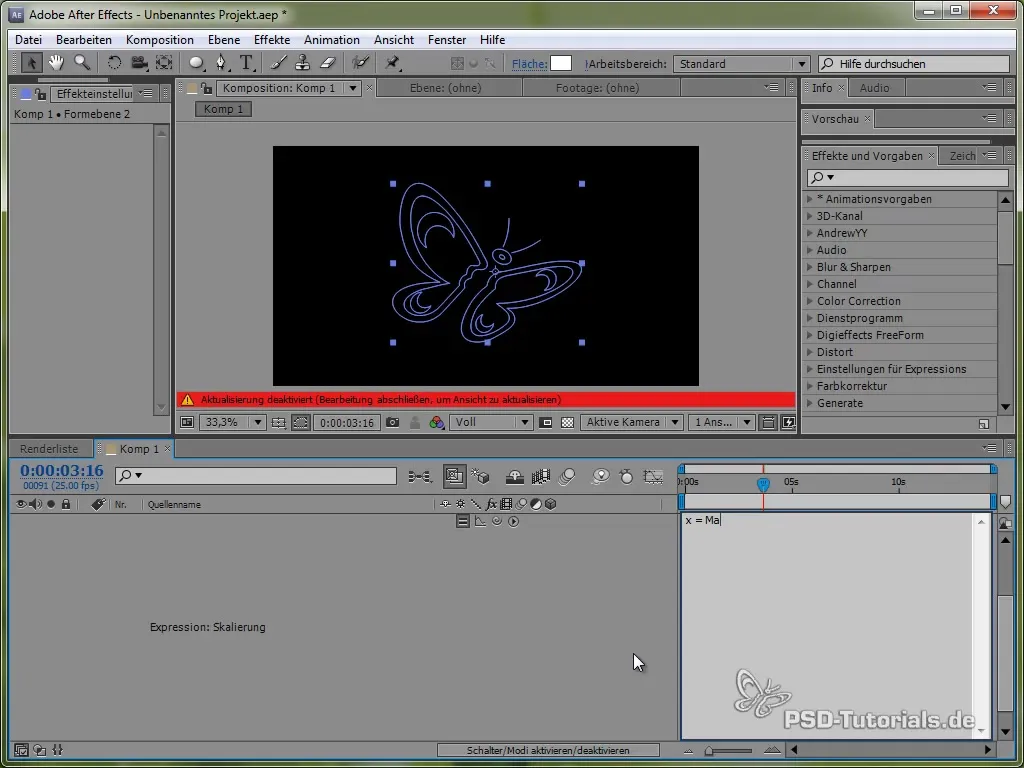
Végső gondolatok
Látható, hogy a trigonometrikus és exponenciális funkciók helyes alkalmazásával nagyon valósághű és érdekes animációk hozhatók létre. Megtanultad, hogyan lehet egy pillangót repülni hagyni, egy libikókát ingatni, és hogyan lehet dolgozni olyan effektekkel, mint az összenyomás és nyújtás.
Összefoglalás - Matematika a kifejezésekben: Trigonometrikus & Exponenciális funkciók
A matematika az After Effects kifejezéseiben lehetőséget ad arra, hogy kreatív és élettel teli animációkat készíts. A trigonometrikus és exponenciális funkciók alapvető fontosságúak ebben. Ebben a bemutatóban tapasztalatokat szereztél ezen matematikai koncepciók gyakorlati alkalmazásáról.
Gyakran ismételt kérdések
Hogyan állíthatok be egy kifejezést az After Effects-ben?Nyomd meg az ALT billentyűt, és kattints arra az órára, amely a tulajdonság mellett van, amelyhez hozzá szeretnéd adni a kifejezést.
Mi a különbség a szinusz és a koszinusz függvények között?A szinusz függvény 0-nál kezdődik, míg a koszinusz függvény 1-nél. Ez kihatással van arra, hogy az animációk hogyan indulnak.
Hogyan hozhatok létre tompító hatásokat?Tompító hatásokat úgy hozhatsz létre, hogy exponenciális függvényeket illesztesz be a kifejezéseidbe, amelyek csökkentik a mozgást idővel.


