Matemātika digitālajā pasaulē spēlē fundamentālu lomu, un it īpaši video rediģēšanā, izmantojot After Effects (AE), tā atver tev pilnīgi jaunas iespējas. Šajā apmācībā tu iemācīsies, kā izmantot trigonometrijas un eksponenciālās funkcijas AE kā izteiksmes, lai radītu apburošas animācijas. Īpaši aizraujošs piemērs būs tauriņa kustība, kas parādīs, kā fiziskās simulācijas var īstenot, izmantojot matemātiku.
Galvenās atziņas
- Trigonometrijas funkcijas, piemēram, sinuss un kosinuss, var izmantot, lai radītu nobīdītas kustības.
- Eksponenciālās funkcijas tiek izmantotas, lai simulētu nomākšanas efektus.
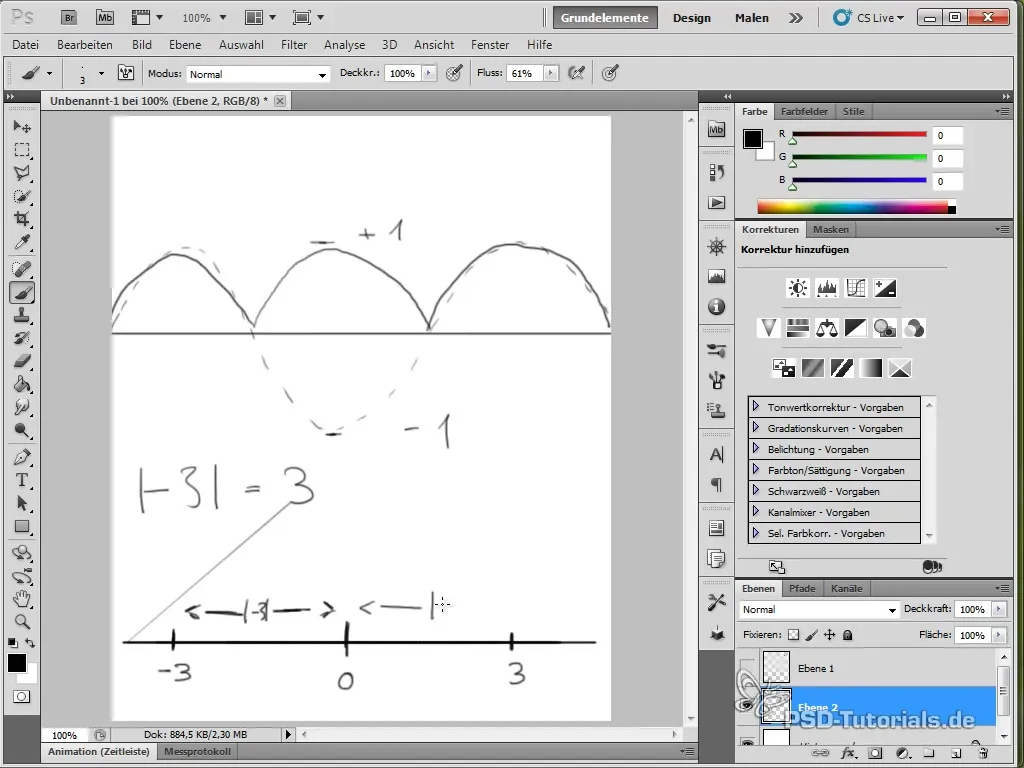
- Absolūtā vērtība funkcijās var palīdzēt sasniegt noteiktus animācijas efektus.
Solim pa solim instrukcija
Pārvietot tauriņu
Lai mūsu tauriņš sāktu pārvietoties, vispirms jānokļūst viņu tā, lai tas kustētos viļņos. Šo viļņu kustību var viegli īstenot, izmantojot izteiksmes.
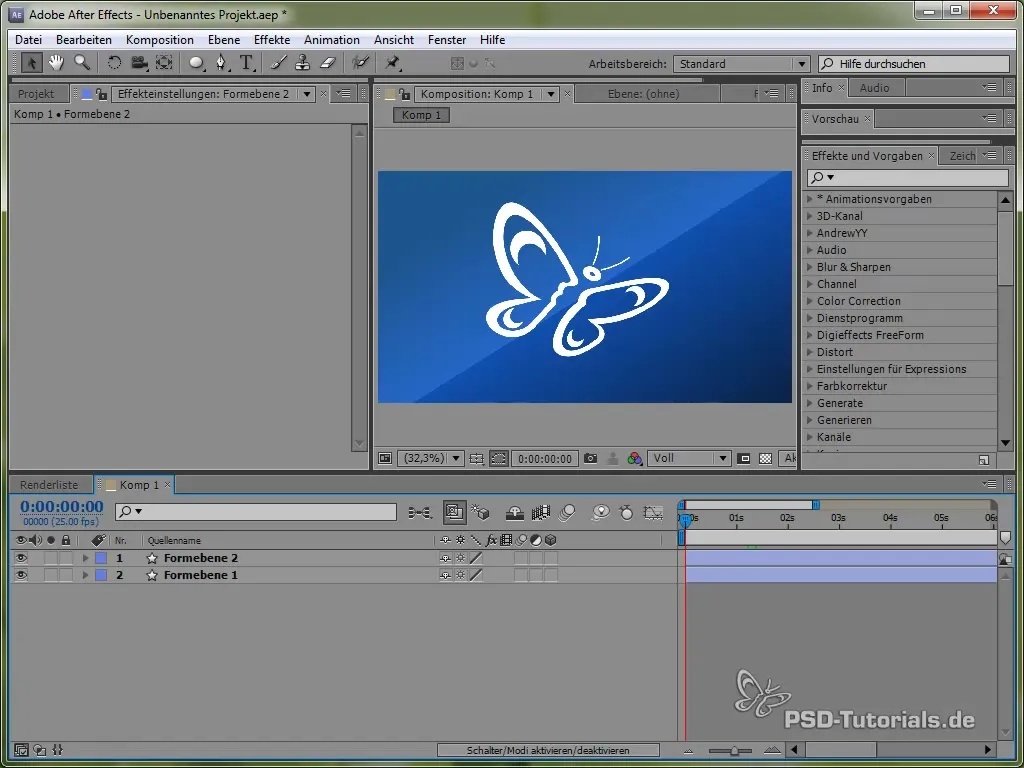
Sāc, atverot tauriņa pozīciju, nospiežot taustiņu “P”. Pēc tam pievieno izteiksmi pozīcijai, nospiežot ALT taustiņu un uzklikšķinot uz pulksteņa ikonas.
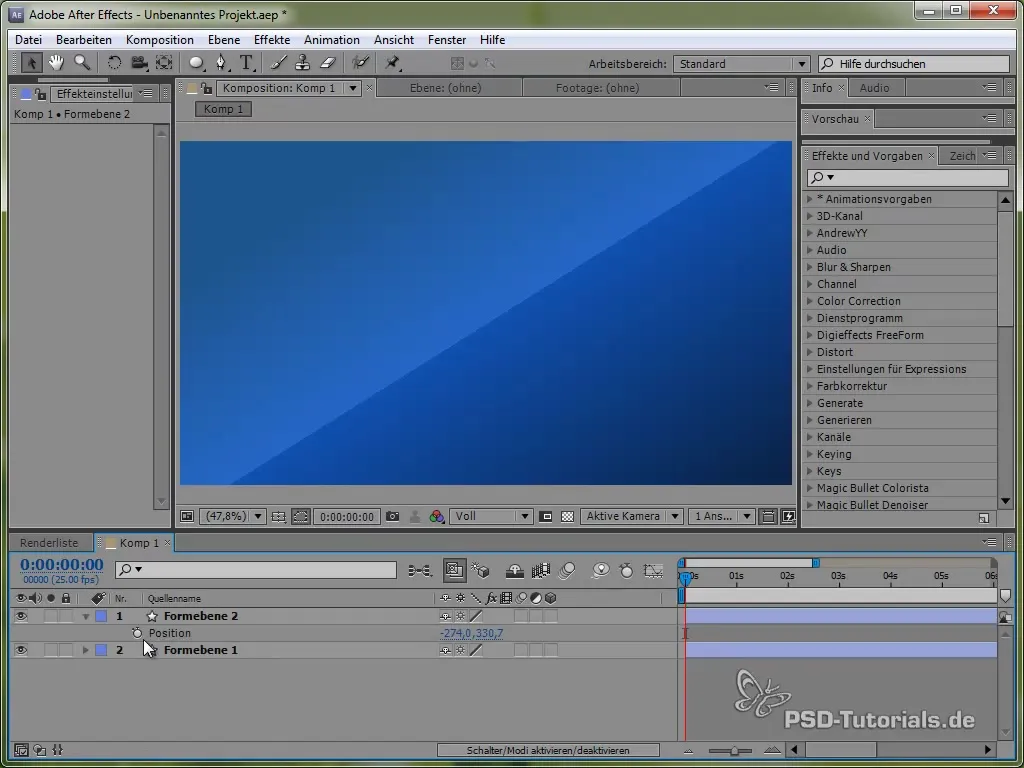
Šim nolūkam mēs vispirms izmantosim laika mainīgo time, reizinot to ar vērtību, kas nosaka kustības ātrumu. Piemēram:
value[0] + time * 150
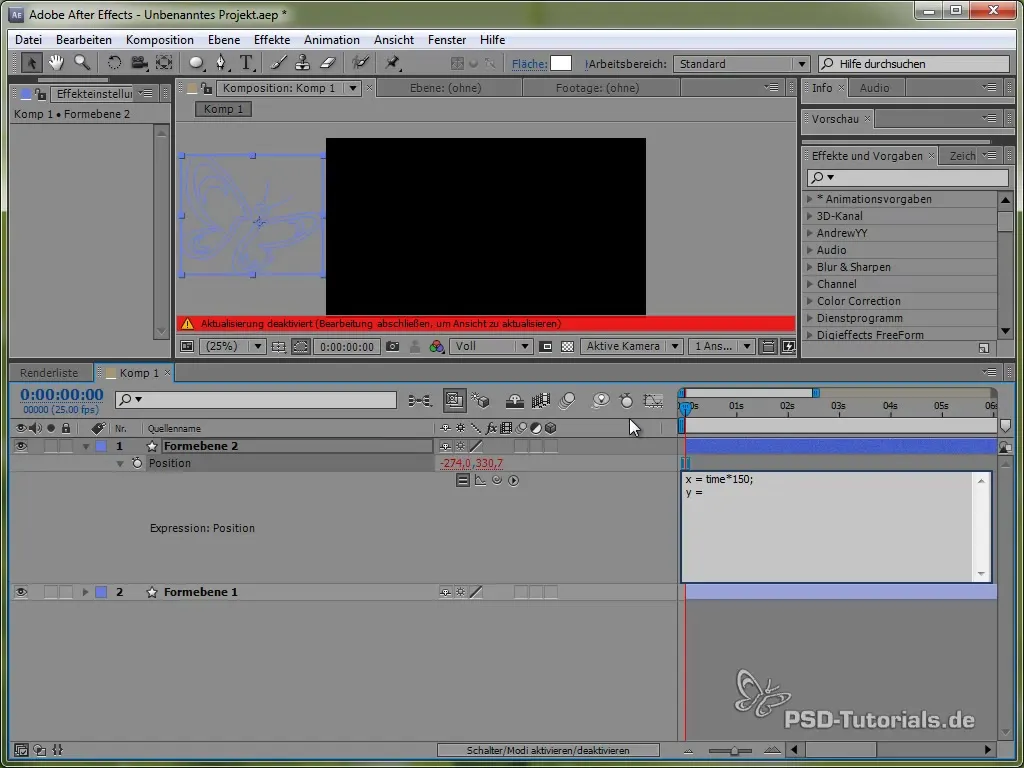
Šis kods nodrošina, ka tauriņš X virzienā kustas konstanti par 150 pikseļiem sekundē. Y virzienā mēs izmantosim sinusa funkciju, kas radīs tauriņa vertikālo kustību un ļaus tam "svārstīties" starp noteiktām vērtībām.
Sinusa funkcijas pielietojums
Y kustību nosaka šāda izteiksme:
value[1] + 40 * Math.sin(2 * Math.PI * time)
Šajā gadījumā Math.sin() veic sinusa funkcijas aprēķinus. Tā svārstās starp -1 un 1 un tiek reizināta ar 40, kas nozīmē, ka tauriņš Y virzienā svārstās starp -40 un 40 pikseļiem.
Kustības grafiku vizualizēt
Lai labāk vizualizētu šo kustību, tu vari aktivizēt grafiku logu After Effects. Tas skaidrāk parādīs sinusa vērtības svārstības.
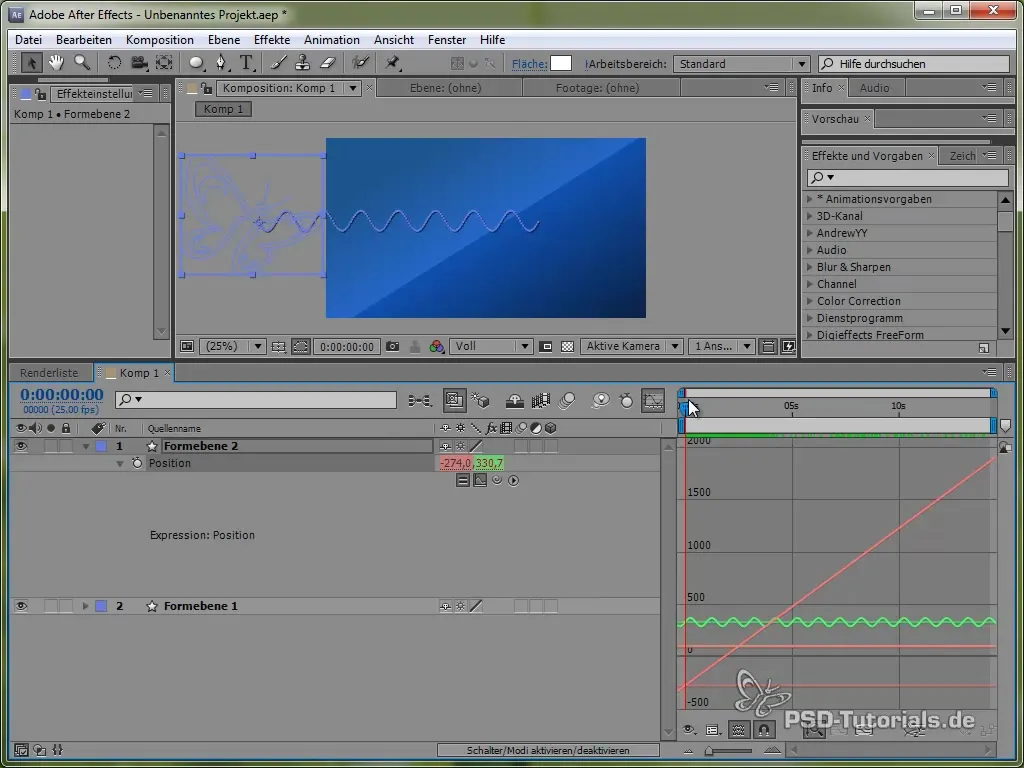
Redzams, ka signāls oscilē un pārvietojas pāri ekrānam.
Amplitūdu un frekvenci mainīt
Tagad tu vari pielāgot amplitūdu, lai radītu dažādas svārstību intensitātes. Ja vēlies, piemēram, laika gaitā palielināt amplitūdu, tu varētu izmantot sekojošo:
40 * (time * 10) * Math.sin(2 * Math.PI * time)
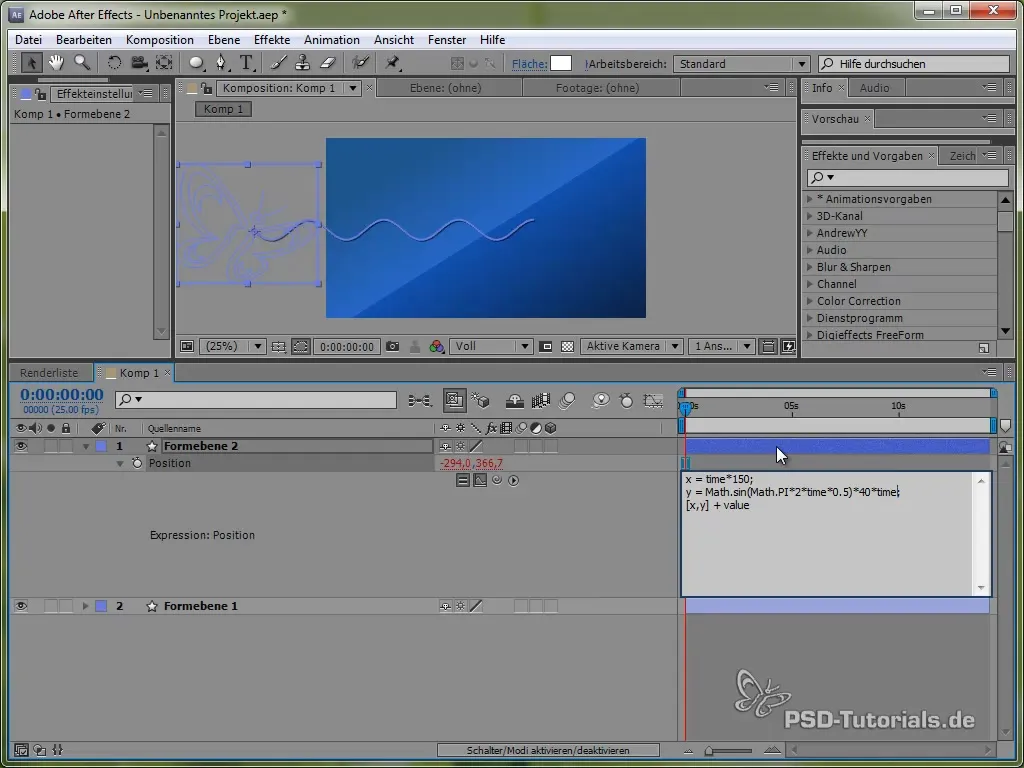
Ar šo amplitūda laika gaitā palielinās, kas nozīmē, ka tauriņš pēc vienas sekundes svārstās par 40 pikseļiem, pēc divām sekundēm par 80 pikseļiem un tā tālāk.
Izveidot svārstošus pendulus
Lai padziļinātu zināšanas par dažādām fiziskām simulācijām, pievērsīsimies svārstoša pendula izveidei. Vispirms uzzīmē plānu stieni un pievieno elipsi tā galā.
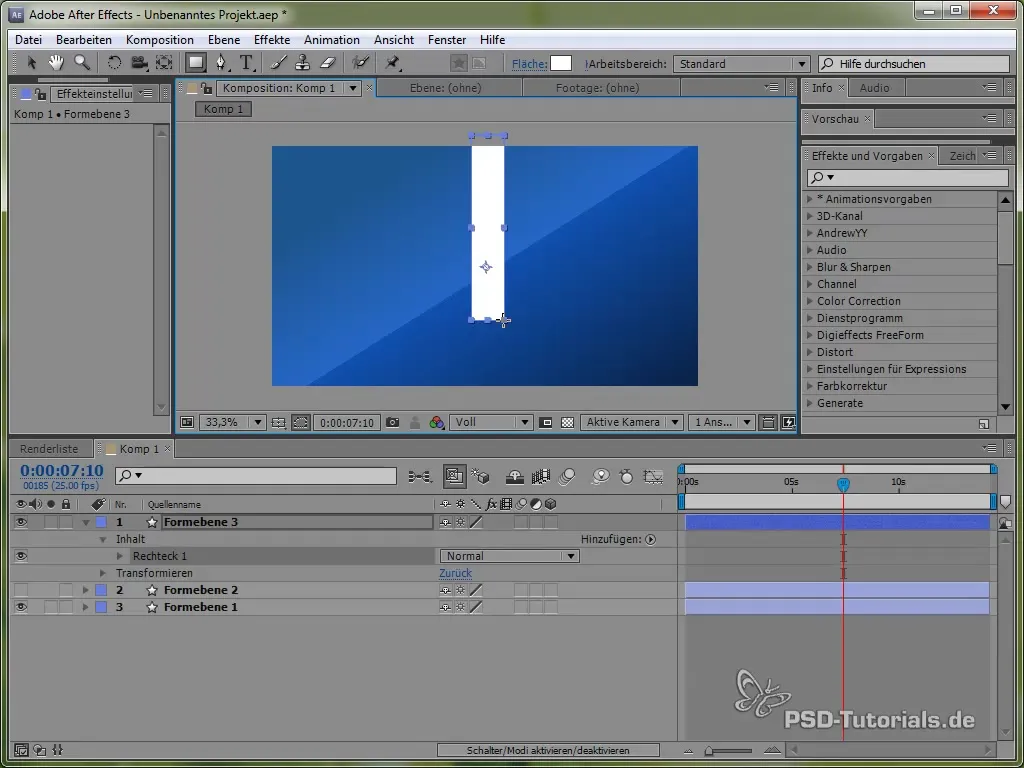
Novieto enkura punktu pendula augšpusē, lai tas varētu svārstīties. To var izdarīt ar enkura punkta rīku.
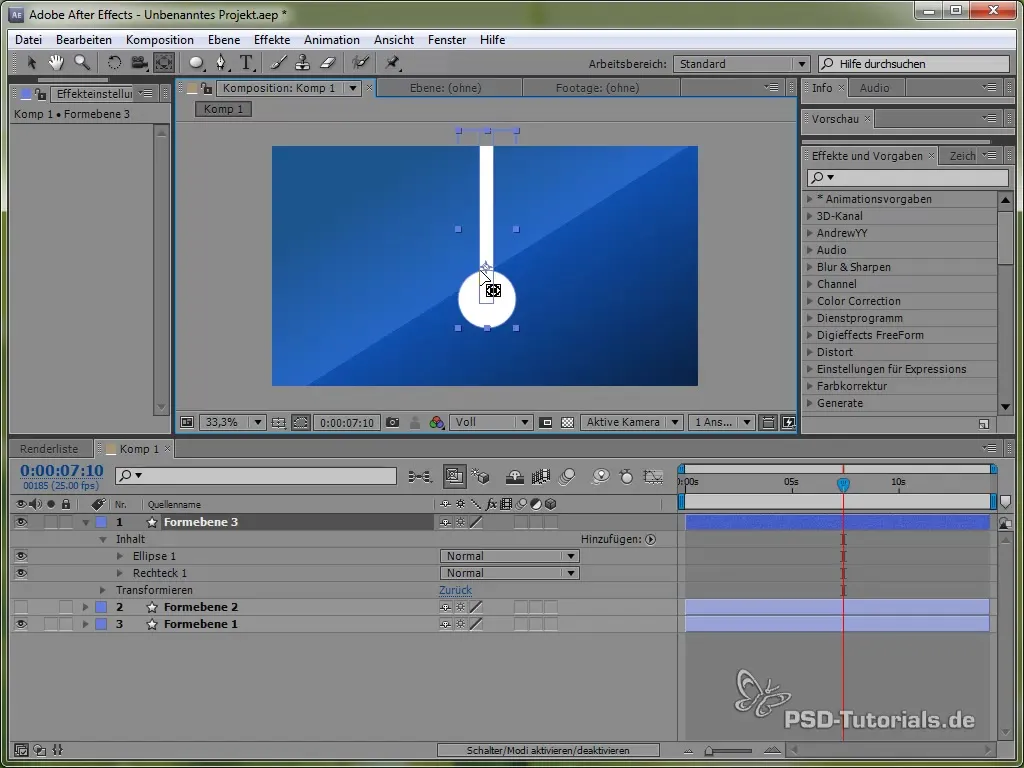
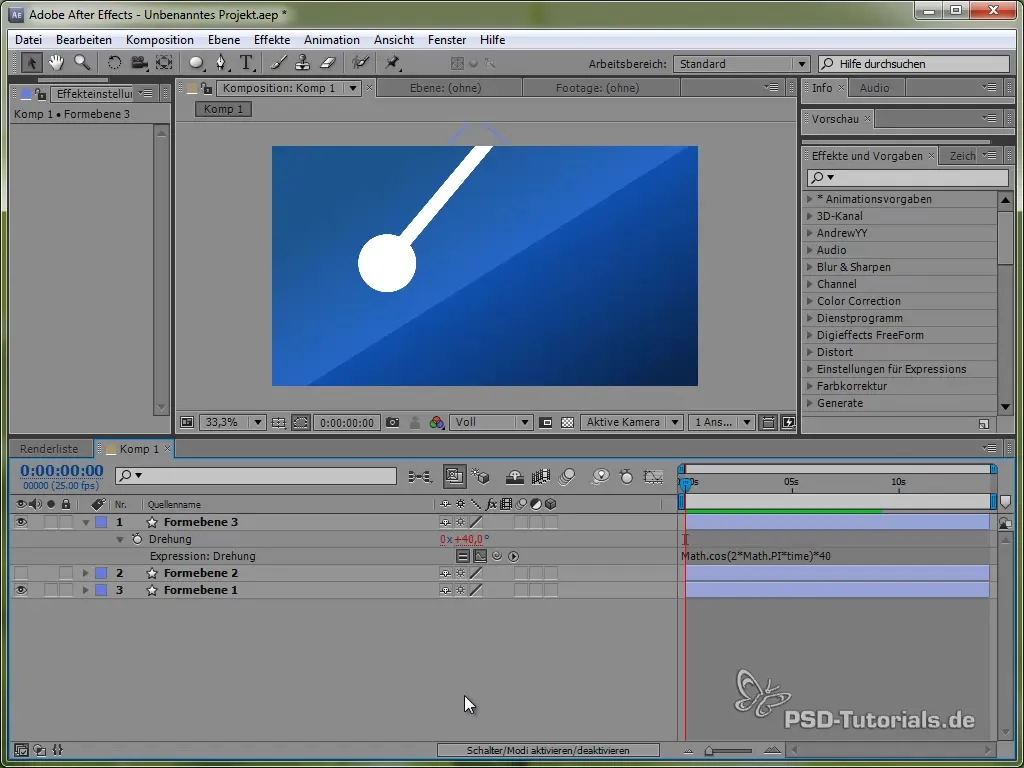
Pēc tam iestati izteiksmi:
value + 40 * Math.cos(2 * Math.PI * time)
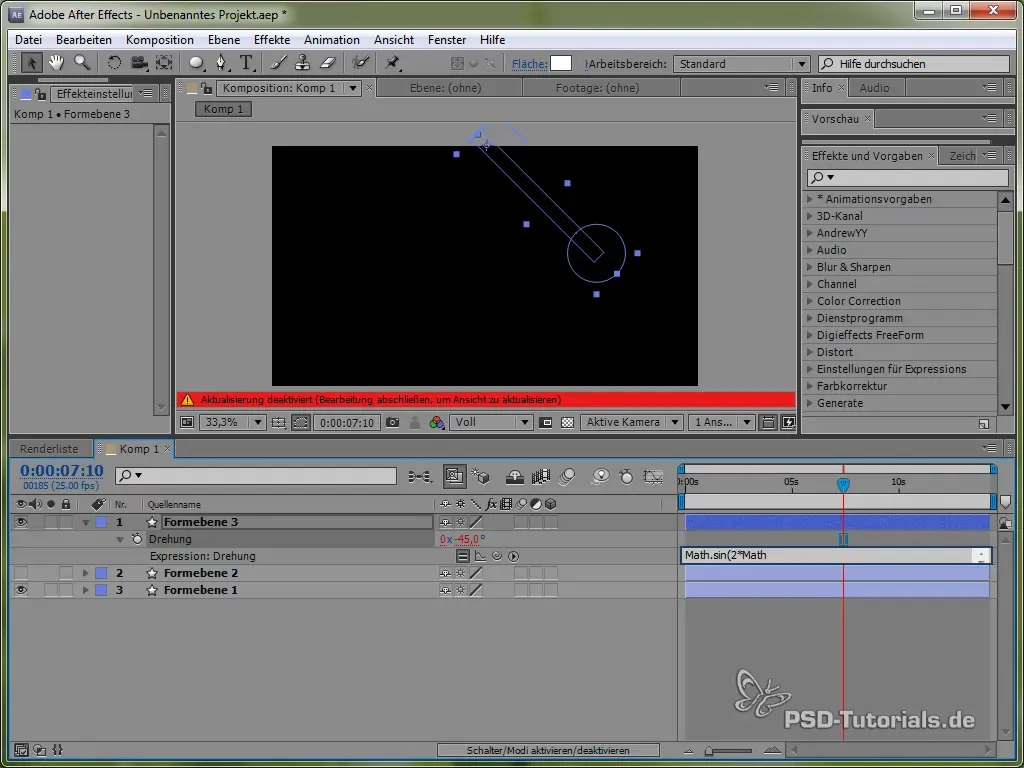
Izmantojot kosinusu, mēs uzsākam svārstīšanas procesu no pozitīva punkta, kas ir reālistiski, jo pendula svārstīšanās sākas augšējā pozīcijā.
Iekļaut nomākšanas efektus
Lai iekļautu nomākšanu svārstījumos, mēs izmantosim eksponenciālo funkciju. Tas padara svārstījumus reālistiskākus, jo vispirms tie ir spēcīgi un pēc tam pamazām samazinās.
Piemēra kods varētu izskatīties šādi:
40 * Math.cos(2 * Math.PI * time) / Math.exp(time)
Šajā gadījumā dalījums ar eksponenciālo funkciju nodrošina pakāpenisku nomākšanu.
Pievienot squash un stretch
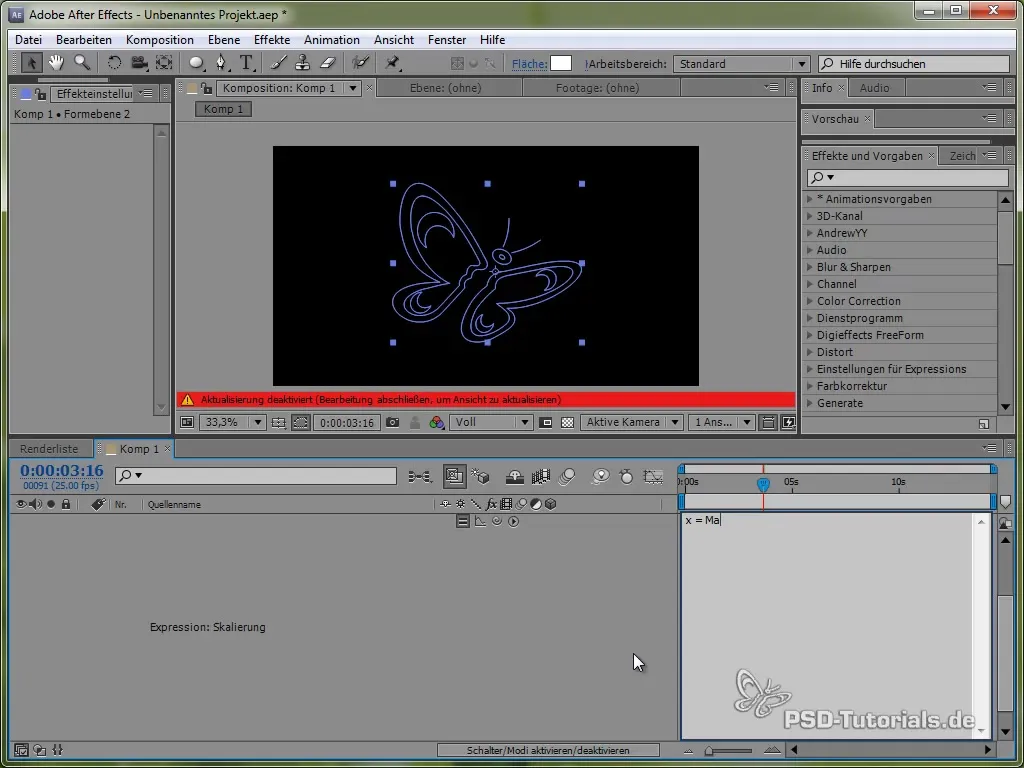
Lai animācijas būtu dzīvīgākas, tu vari arī pievienot squash and stretch efektu. To vari sasniegt, mainot tauriņa mērogu.
Tu dari to, pielietojot izteiksmi uz mērogošanas rādītāju, kuru var pielietot gan uz x, gan uz y vērtībām, izmantojot sinusa vai kosinusa funkciju.
Noslēguma domas
Redzams, ka, pareizi pielietojot trigonometrijas un eksponenciālās funkcijas, var radīt ļoti reālistiskas un interesantas animācijas. Tu esi iemācījies, kā panākt, lai tauriņš lido, pendula svārstās un kā strādāt ar efektiem, piemēram, squash and stretch.
Kopsavilkums - Matemātika izteiksmēs: Trigonometrijas & Eksponenciālās funkcijas
Matemātika, kontekstā ar izteiksmēm After Effects, dod tev iespēju radīt radošas un dzīvīgas animācijas. Trigonometrijas un eksponenciālās funkcijas ir šajā procesā būtiskas. Šajā apmācībā tu ieguvi pieredzi, izmantojot šos matemātiskos konceptus praksē.
Biežāk uzdotie jautājumi
Kā es varu iestatīt izteiksmi After Effects?Nospied ALT taustiņu un uzklikšķini uz pulksteņa ikonas blakus īpašībai, kurai vēlies pievienot izteiksmi.
Kādas ir atšķirības starp sinusa un kosinusa funkcijām?Sinusa funkcija sākas pie 0, kamēr kosinusa funkcija sākas pie 1. Tam ir ietekme uz to, kā animācijas sākas.
Kā es varu izveidot nomākšanas efektus?Tu vari radīt nomākšanas efektus, ievietojot eksponenciālās funkcijas savās izteiksmēs, kas samazina kustību laika gaitā.


