Matematica în expresii: concepte trigonometrice și exponențiale

Matematica joacă un rol fundamental în lumea digitală și, mai ales în editarea video cu After Effects (AE), îți deschide cu totul noi posibilități. În acest tutorial vei învăța cum să folosești funcții trigonometrice și funcții exponențiale în AE ca Expressions pentru a crea animații fascinante. Un exemplu deosebit de interesant va fi mișcarea unei fluturaș, care îți va arăta cum simulările fizice pot fi realizate cu ajutorul matematicii.

Principalele concluzii

• Funcțiile trigonometrice, cum ar fi sinus și cosinus, pot fi folosite pentru a genera mișcări decalate.
• Funcțiile exponențiale sunt utilizate pentru a simula efecte de atenuare.
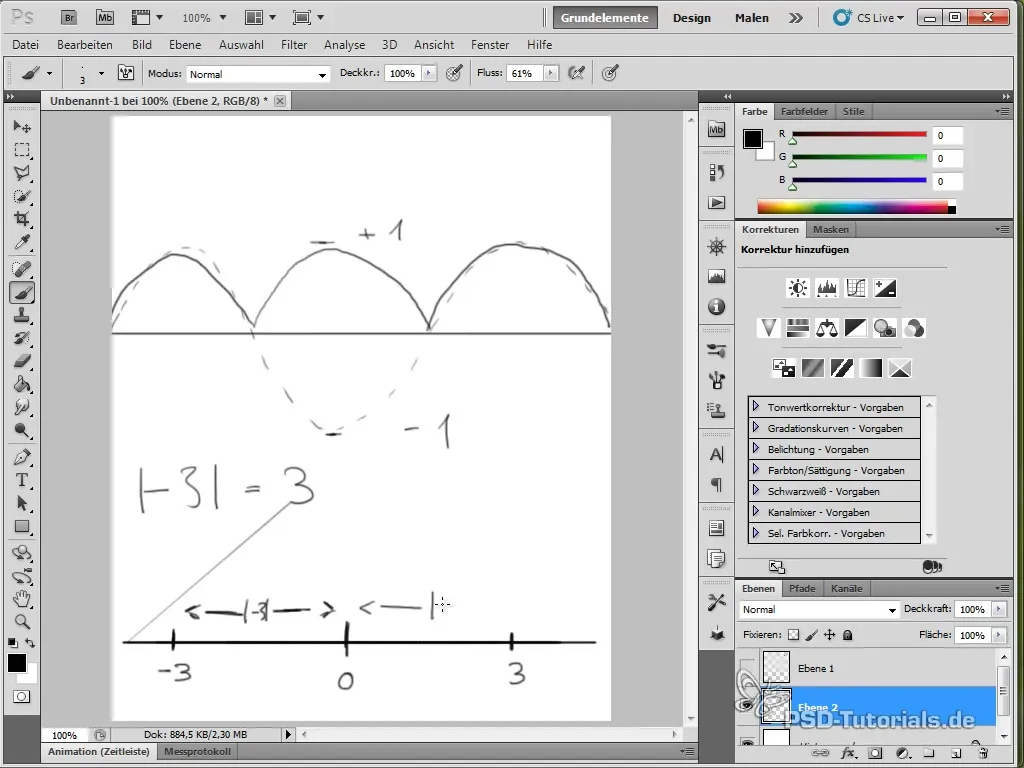
• Utilizarea valorilor absolute în funcții poate ajuta la obținerea unor efecte de animație specifice.

Ghid pas cu pas

Pune în mișcare fluturașul

Pentru a pune fluturașul nostru în mișcare, trebuie mai întâi să-l animezi în așa fel încât să se miște într-o undă. Această mișcare ondulată poate fi realizată cu ușurință prin Expressions.

Începe prin a deschide poziția fluturașului apăsând tasta „P”. Apoi, setează o Expression pentru poziție apăsând tasta ALT și făcând clic pe ceas.

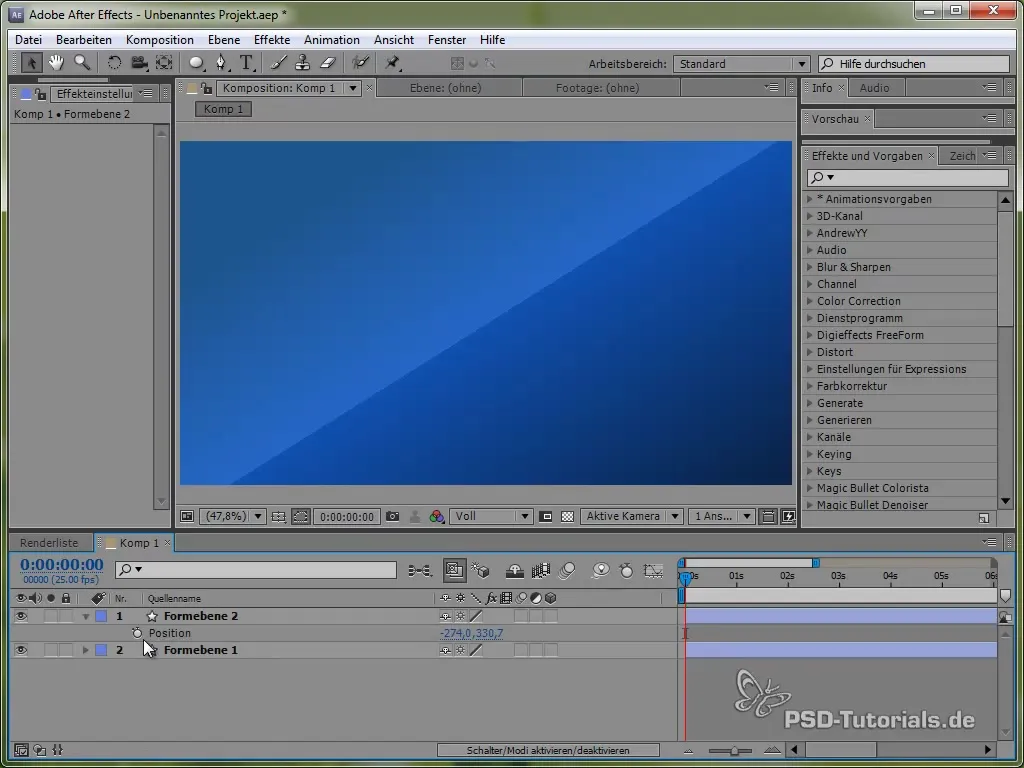
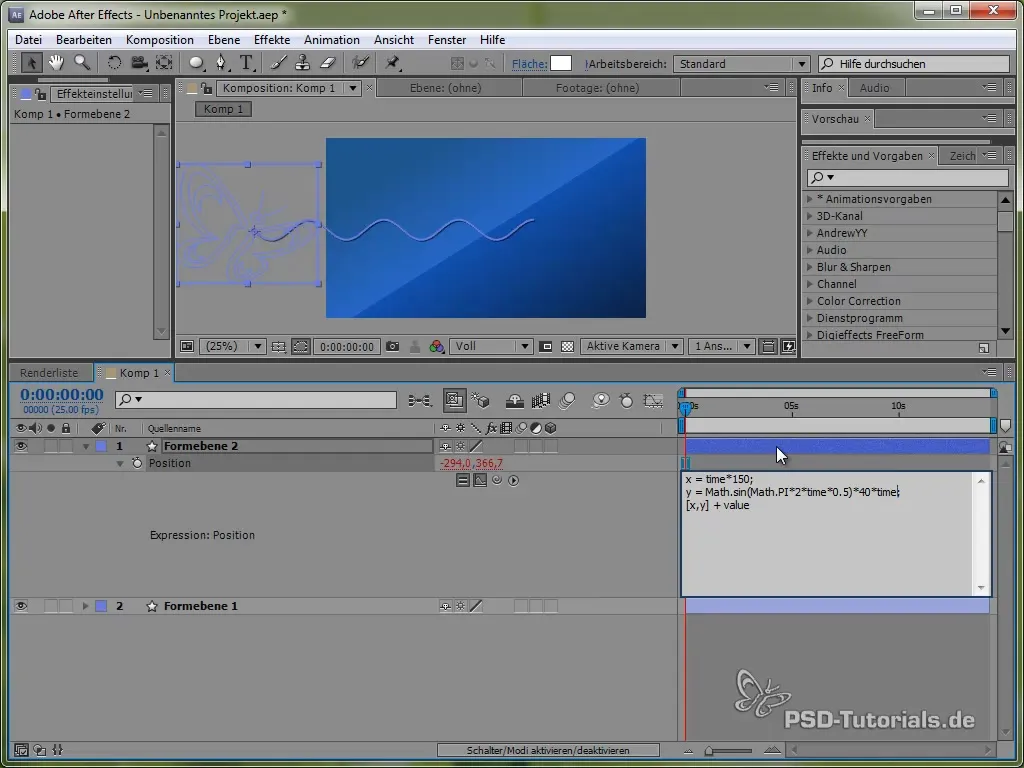
Pentru aceasta, folosim mai întâi variabila de timp time, înmulțită cu o valoare care stabilește viteza mișcării. De exemplu:

value[0] + time * 150

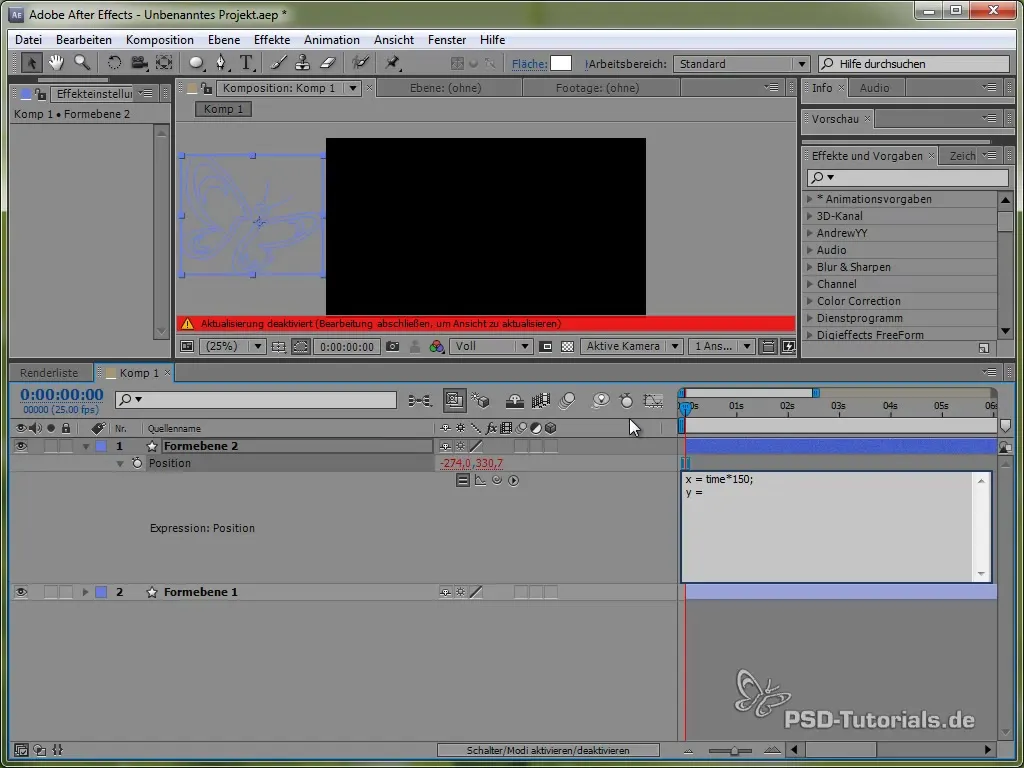
Aceast cod face ca fluturașul să se miște constant în direcția X cu 150 pixeli pe secundă. Pentru direcția Y, vom folosi o funcție sinus, care va crea mișcarea verticală a fluturașului și îl va „clătina” între anumite valori.

Aplicarea funcției sinus

Mișcarea Y este definită prin următoarea Expression:

value[1] + 40 * Math.sin(2 * Math.PI * time)

Aici, Math.sin() implementează funcția sinus. Aceasta variază între -1 și 1 și este înmulțită cu 40, ceea ce înseamnă că fluturașul va „clătina” între -40 și 40 pixeli în direcția Y.

Vizualizarea graficii mișcării

Pentru a vizualiza mai bine această mișcare, poți activa fereastra graficului în After Effects. Aceasta îți va arăta mai clar fluctuațiile valorii sinus.

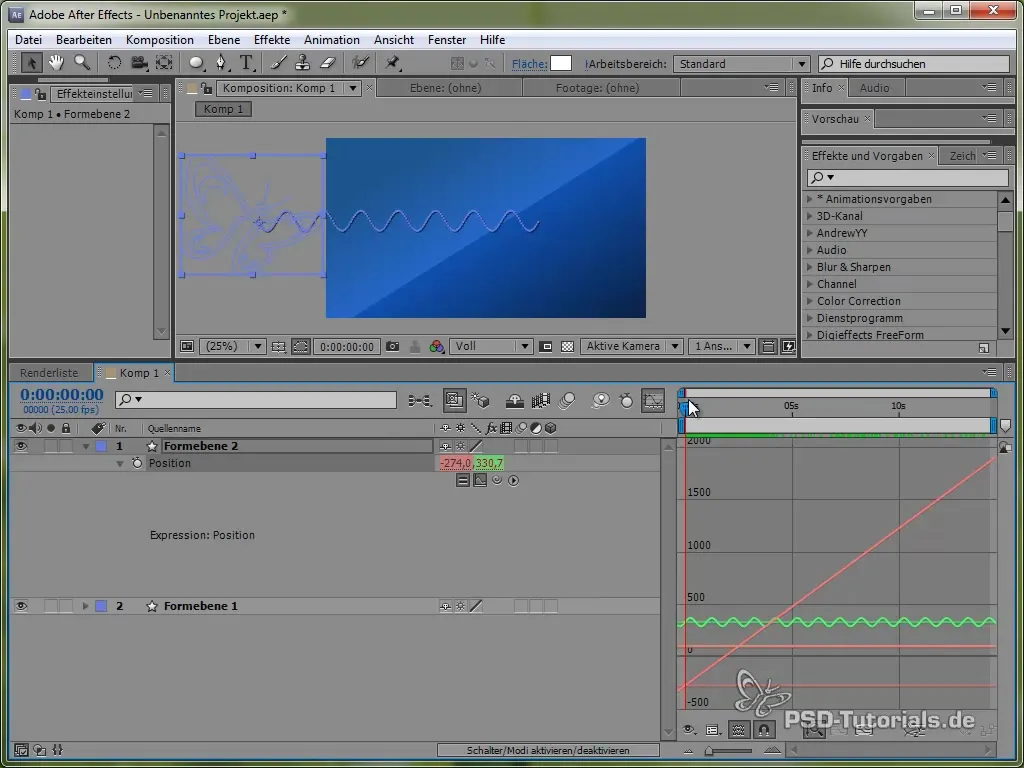
Se vede că semnalul oscilează și se mișcă pe ecran.

Varierea amplitudinii și frecvenței

Acum poți ajusta amplitudinea pentru a genera oscilații de diferite intensități. De exemplu, dacă vrei să crești amplitudinea în timp, ai putea folosi următoarea expresie:

40 * (time * 10) * Math.sin(2 * Math.PI * time)

Așadar, amplitudinea va crește în timp, ceea ce face ca fluturașul să oscileze 40 de pixeli după o secundă, 80 de pixeli după două secunde și așa mai departe.

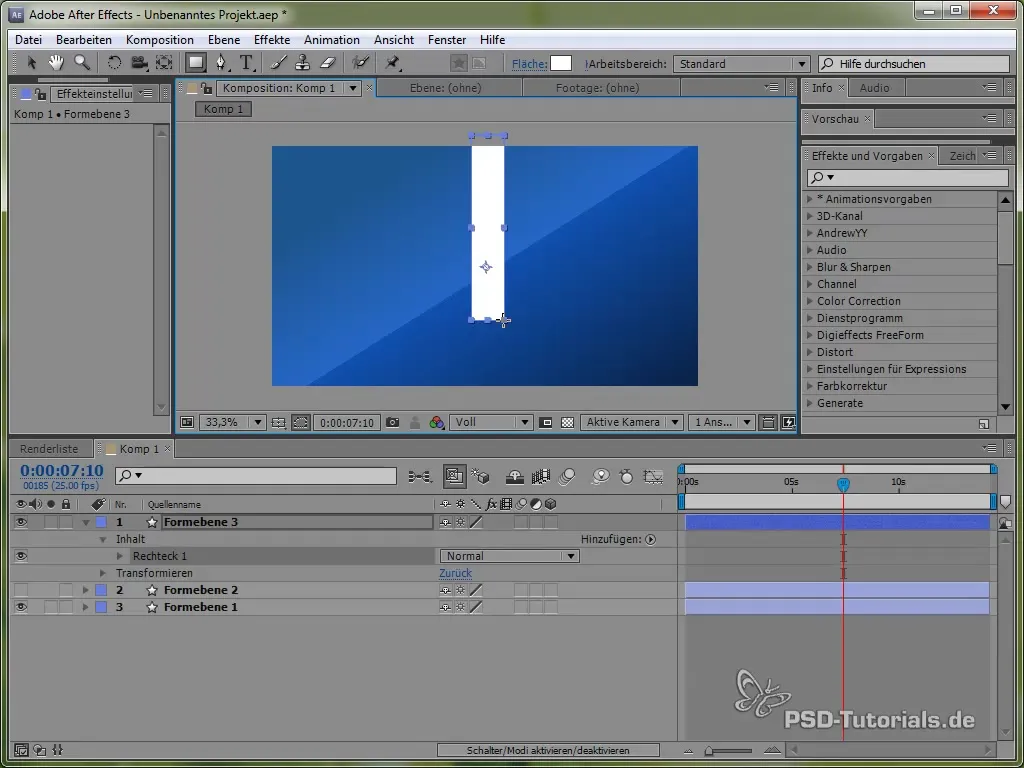
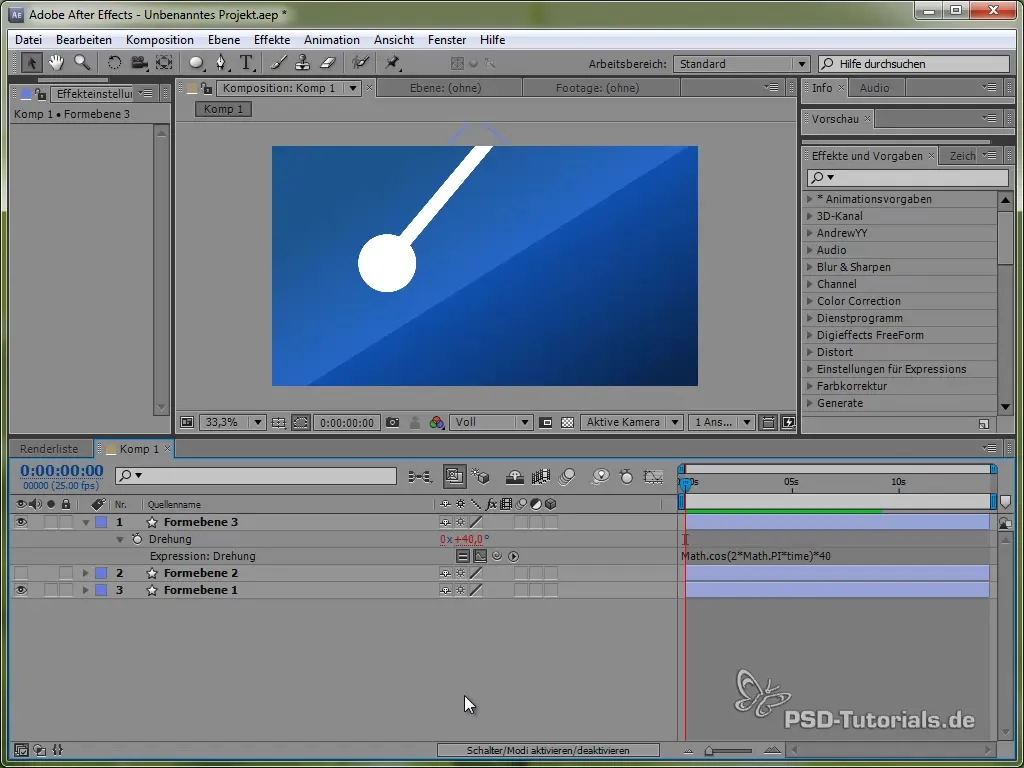
Crearea unui pendul

Pentru a aprofunda utilizarea diferitelor simulări fizice, ne îndreptăm acum către crearea unui pendul. Desenează mai întâi o bară subțire și adaugă o elipsă la capătul acesteia.

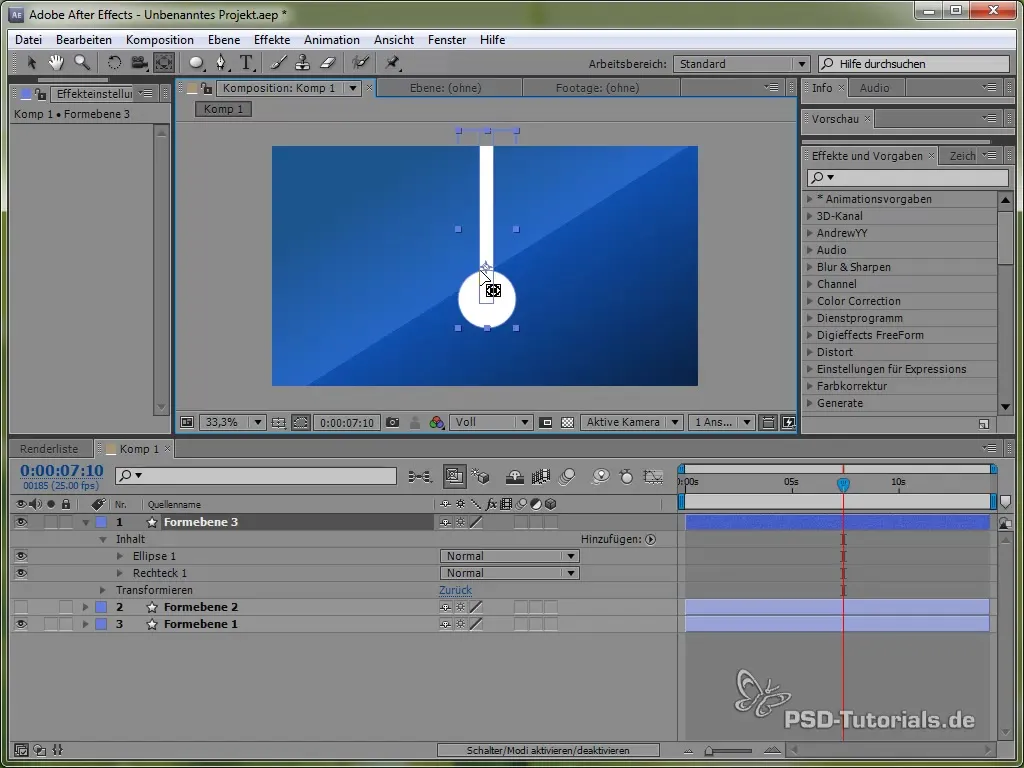
Poziționează punctul de ancorare deasupra pendulului, astfel încât să poată oscila. Acest lucru se face cu instrumentul pentru punctul de ancorare.

Apoi, setează expresia:

value + 40 * Math.cos(2 * Math.PI * time)

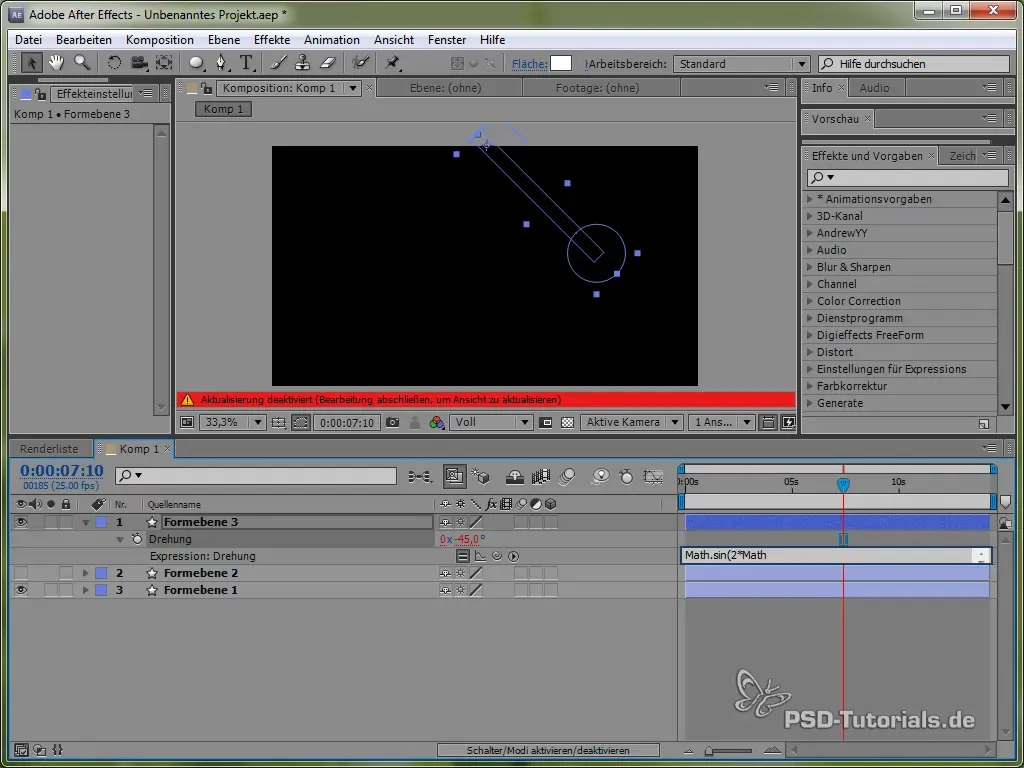
Prin cosinus, începem procesul de oscilație dintr-un punct pozitiv, ceea ce este realist, deoarece pendulul începe să oscileze de sus.

Adăugarea efectelor de atenuare

Pentru a integra atenuarea în oscilație, folosim funcția exponențială. Astfel, oscilația va părea mai realistă, deoarece la început este puternică și, în cele din urmă, scade.

Un cod exemplu ar putea arăta astfel:

40 * Math.cos(2 * Math.PI * time) / Math.exp(time)

Aici, împărțirea prin funcția exponențială asigură o atenuare lentă.

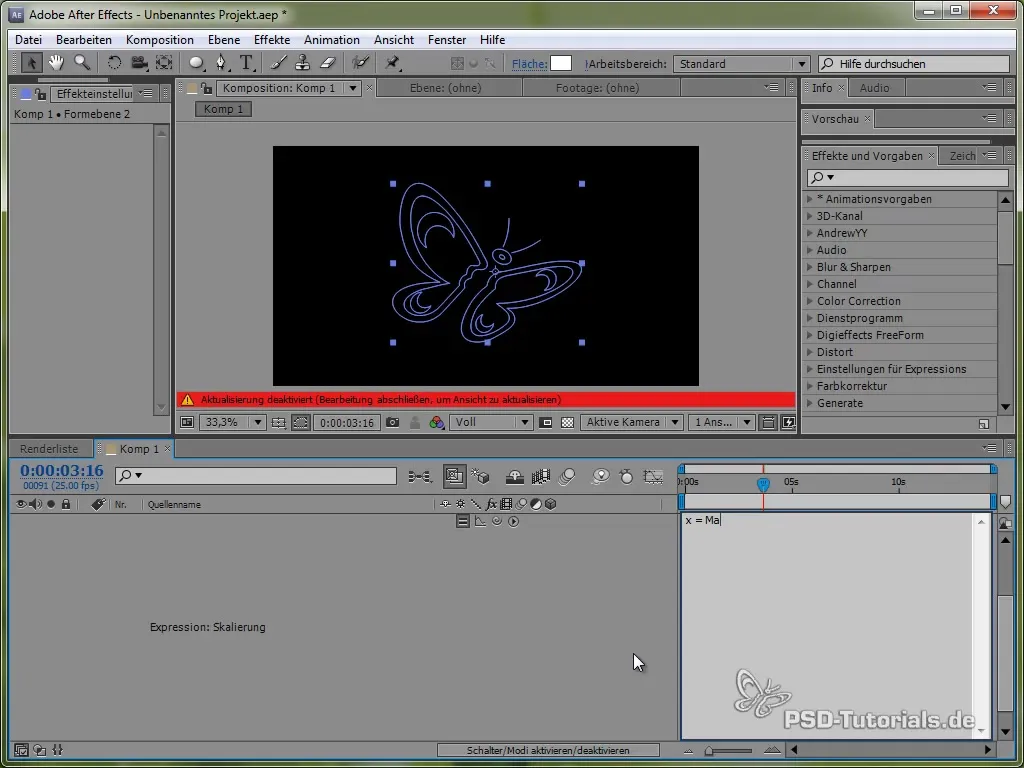
Adăugarea efectului de Squash și Stretch

Pentru animații mai vii, poți adăuga și efectul Squash and Stretch. Acest lucru poate fi realizat prin scalarea fluturașului.

Faci acest lucru aplicând o Expression pe scalarea scalei, care poate fi aplicată atât pe valori x, cât și pe valori y, folosind o funcție sinus sau cosinus.

Gânduri finale

Se vede că prin aplicarea corectă a funcțiilor trigonometrice și exponențiale, pot fi create animații foarte realiste și interesante. Ai învățat cum să faci un fluturaș să zboare, cum să faci un pendul să oscileze și cum să lucrezi cu efecte precum Squash and Stretch.

Sumar - Matematica în Expressions: Funcții trigonometrice & Exponențiale

Matematica în contextul Expressions în After Effects îți deschide posibilitatea de a crea animații creative și vibrante. Funcțiile trigonometrice și exponențiale sunt esențiale în acest sens. În acest tutorial, ai dobândit experiență în utilizarea acestor concepte matematice în practică.