Matematika v izrazih: Trigonometrične in eksponentne koncepte

Matematika ima v digitalnem svetu temeljno vlogo, zlasti pri obdelavi videa z After Effects (AE), saj ti odpira povsem nove možnosti. V tem vodiču se boš naučil, kako lahko trigonometrične in eksponentne funkcije v AE uporabljaš kot izraze, da ustvariš fascinantne animacije. Posebno zanimiv primer bo gibanje metulja, ki ti bo pokazal, kako lahko fizične simulacije uresničimo s pomočjo matematike.

Najpomembnejše spoznanje

• Trigonometrične funkcije, kot sta sinus in kosinus, lahko uporabimo za ustvarjanje zamaknjene gibanja.
• Eksponentne funkcije se uporabljajo za simulacijo dušilnih učinkov.
• Uporaba absolutnih vrednosti v funkcijah lahko pomaga pri doseganju določenih animacijskih učinkov.

Navodila po korakih

Metulja spravimo v gibanje

Da našega metulja spraviš v gibanje, ga moraš najprej tako animirati, da se premika v valovih. To valovno gibanje je mogoče brez večjih naporov realizirati s pomočjo izrazov.

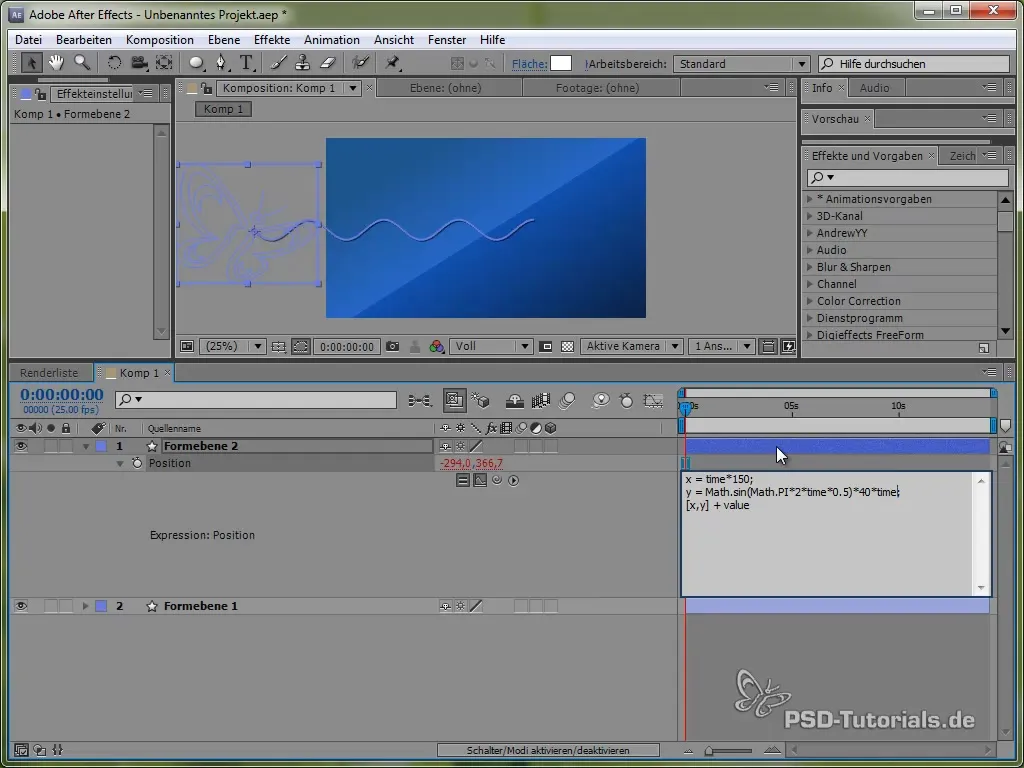
Začnite tako, da odprete pozicijo metulja s pritiskom na tipko „P“. Nato vnesite izraz za pozicijo tako, da pritisnete tipko ALT in kliknete na uro.

Za to najprej uporabimo časovno spremenljivko time, pomnoženo z vrednostjo, ki določa hitrost gibanja. Na primer:

value[0] + time * 150

Ta koda povzroči, da se metulj konstantno premika v X-tekmi za 150 pikslov na sekundo. Za Y-tekmo bomo uporabili sinusno funkcijo, ki ustvari vertikalno gibanje metulja in ga „zibne“ med določenimi vrednostmi.

Uporaba sinusne funkcije

Y-gibanje je definirano z naslednjim izrazom:

value[1] + 40 * Math.sin(2 * Math.PI * time)

Tukaj Math.sin() implementira sinusno funkcijo. Variira med -1 in 1 ter se množi s 40, kar pomeni, da se metulj v Y-tekmi zibne med -40 in 40 pikslov.

Vizualizacija gibanja

Da bi to gibanje bolje vizualiziral, lahko aktiviraš okno grafov v After Effects. To ti jasno pokaže nihanje sinusne vrednosti.

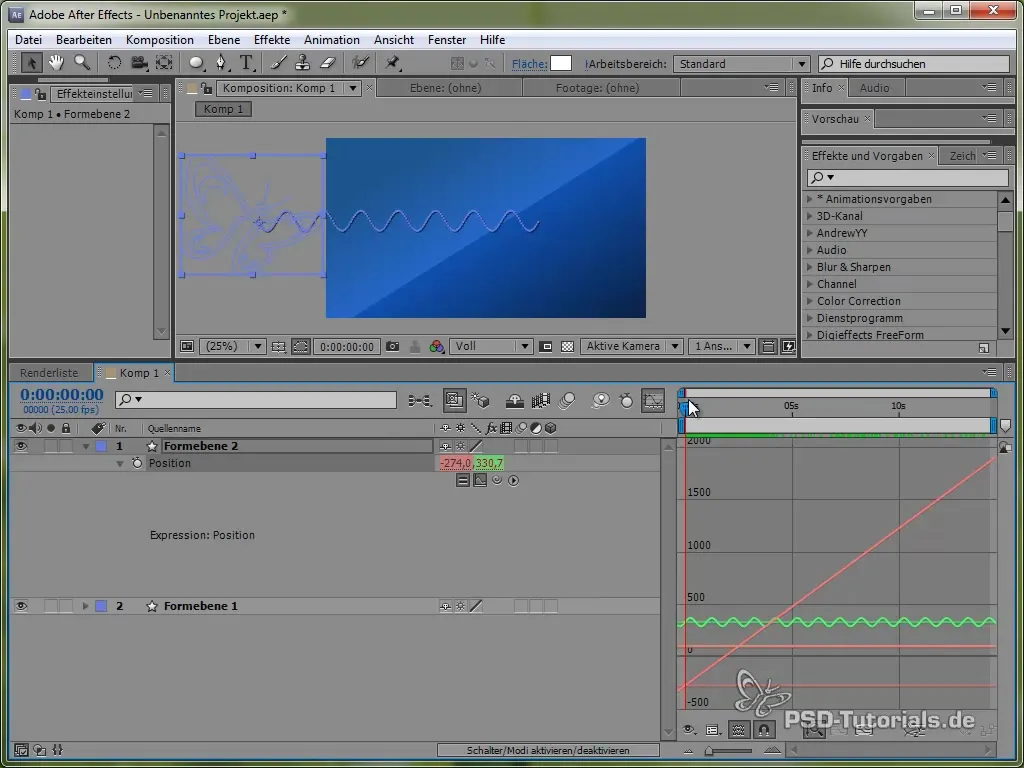
Videti je, da signal oscila in se premika čez zaslon.

Variacija amplitude in frekvence

Zdaj lahko prilagodiš amplitudo, da ustvariš različne močne zibljenja. Če želiš na primer amplitude s časom povečati, lahko uporabiš naslednje:

40 * (time * 10) * Math.sin(2 * Math.PI * time)

To bo povzročilo naraščanje amplitude s časom, kar pomeni, da se bo metulj po eni sekundi zibnil za 40 pikslov, po dveh sekundah za 80 pikslov in tako naprej.

Ustvarjanje nihala

Da bi poglobili delo z različnimi fizičnimi simulacijami, se zdaj posvetimo ustvarjanju nihala. Najprej nariši tanek palec in na njegovem koncu dodaj elipso.

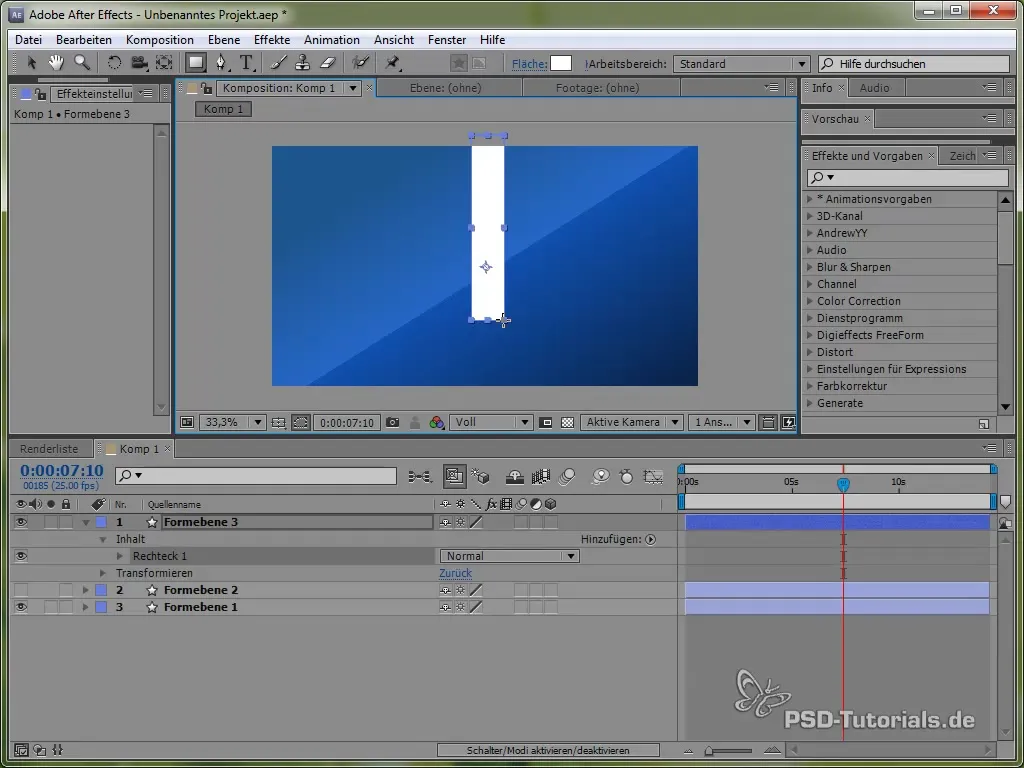
Postavi težišče na vrh nihala, tako da lahko ziba. To lahko storiš z orodjem za težišče.

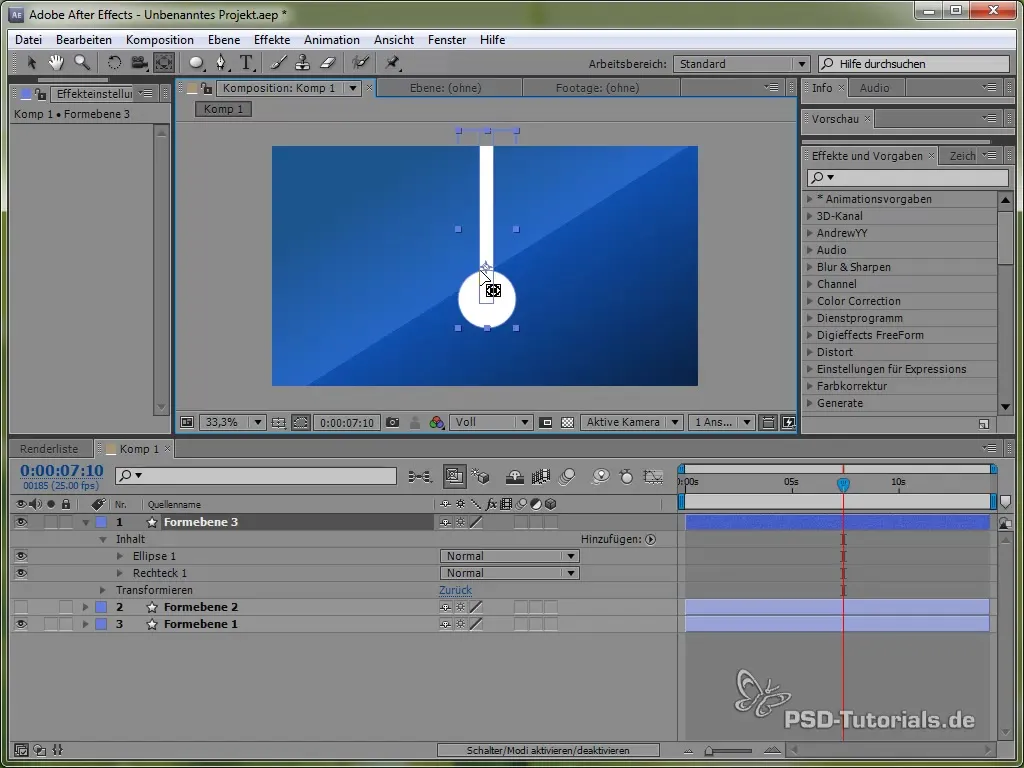
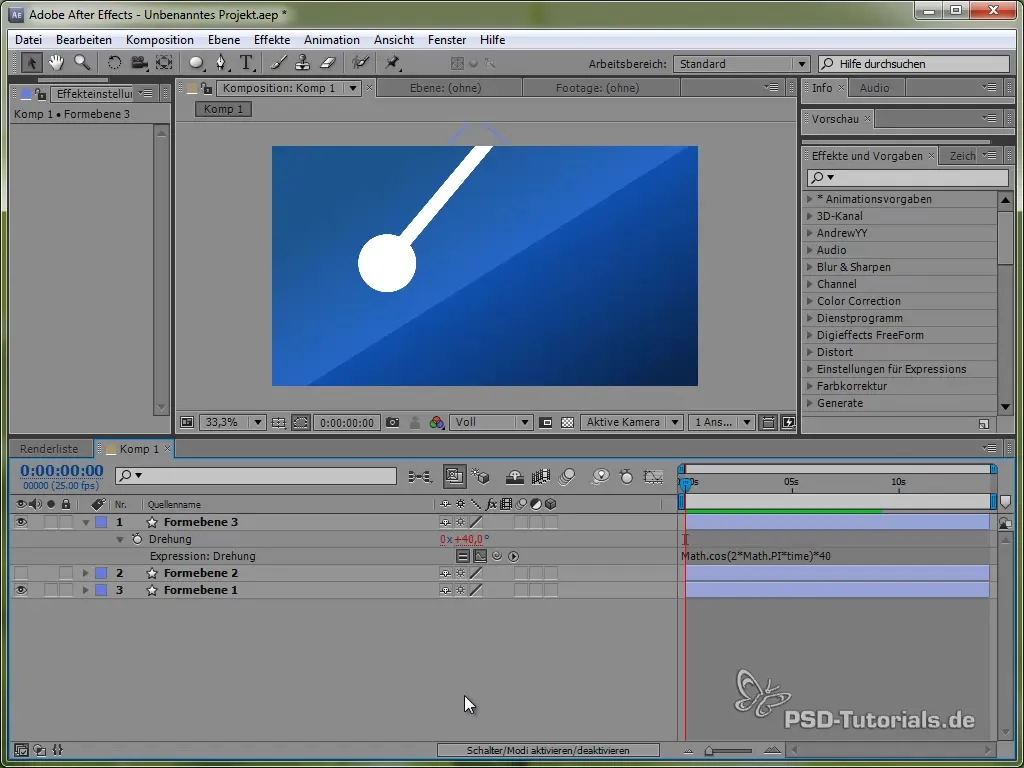
Nato vnesi izraz:

value + 40 * Math.cos(2 * Math.PI * time)

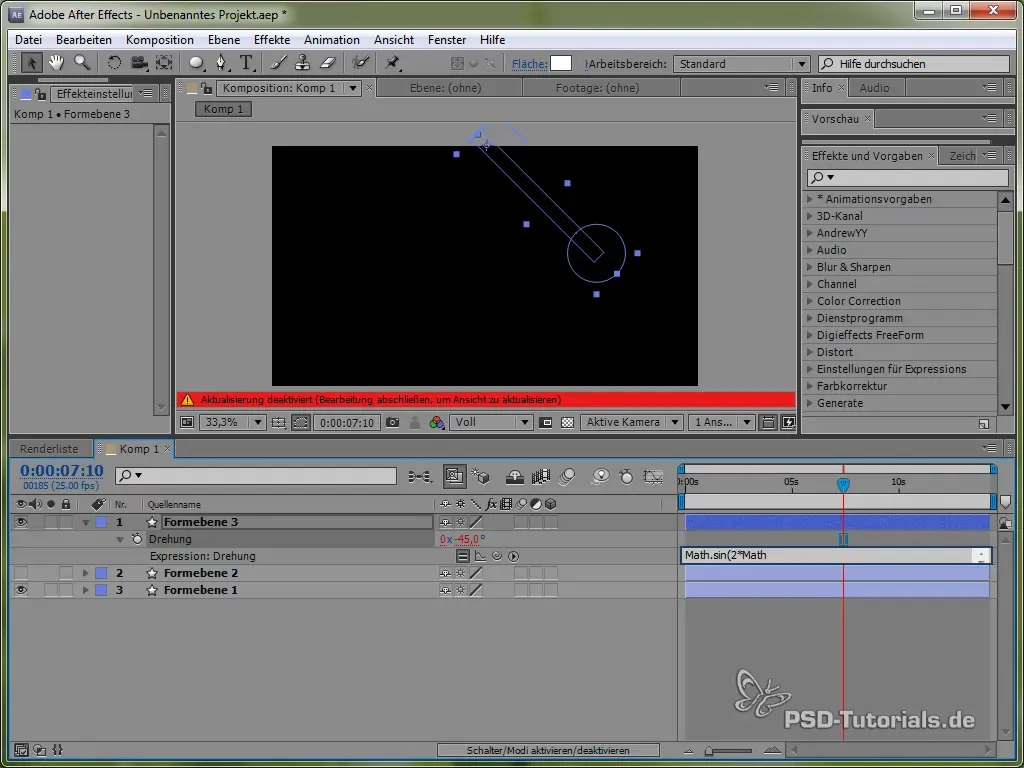
Z uporabo kosinusa začenjamo postopek zibanja iz pozitivne točke, kar je realistično, saj se nihalo začne zibati od vrha.

Vstavljanje dušilnih učinkov

Da bi v zibanje vključili dušenje, uporabljamo eksponentno funkcijo. To daje gibanju bolj realističen videz, saj je na začetku močno in postopoma upada.

Primer kode bi izgledal takole:

40 * Math.cos(2 * Math.PI * time) / Math.exp(time)

Tukaj deljenje z eksponentno funkcijo zagotavlja počasno dušenje.

Dodajanje squashe in stretch

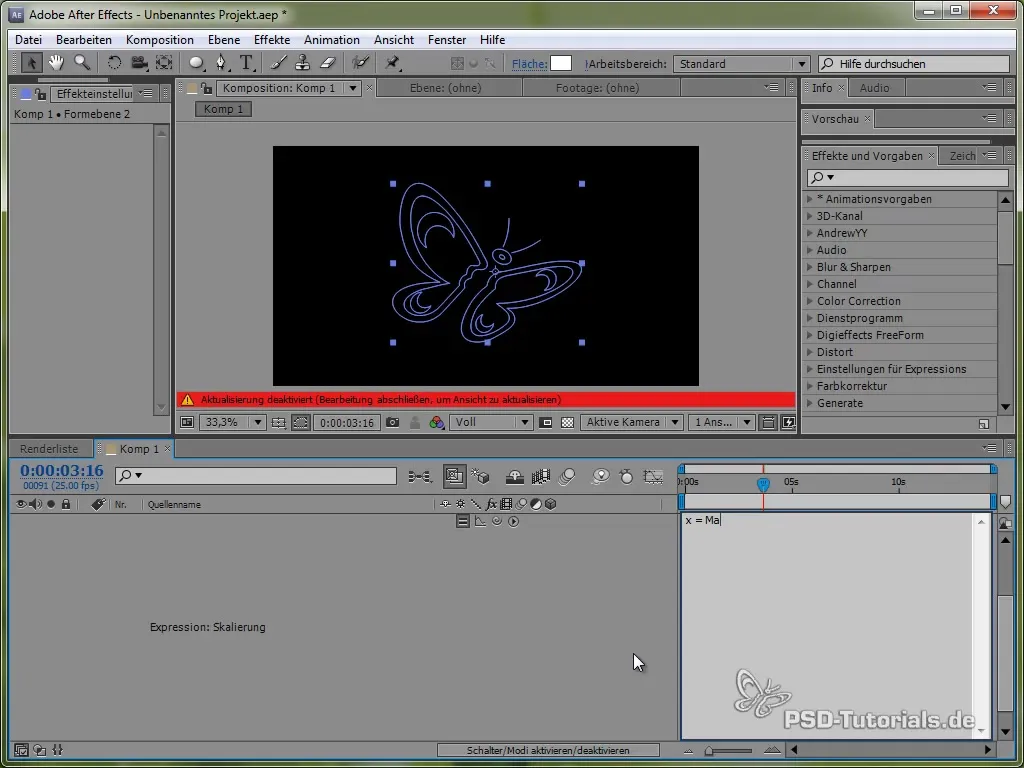
Za bolj živahne animacije lahko dodaš tudi efekt squasha in stretch. To lahko dosežeš s spreminjanjem velikosti metulja.

To storiš z aplikacijo izraza na merilo, ki ga lahko uporabiš tako za x- kot za y-vrednosti, pri čemer uporabiš sinusno ali kosinusno funkcijo.

Zaključne misli

Videti je, da lahko z pravilno uporabo trigonometričnih in eksponentnih funkcij ustvarimo zelo realistične in zanimive animacije. Naučil si se, kako spraviti metulja v zrak, kako zibati nihalo in kako delovati z efekti, kot sta squash in stretch.

Povzetek - Matematika v izrazih: Trigonometrične & eksponentne funkcije

Matematika v kontekstu izrazov v After Effects ti odpira možnost za ustvarjanje kreativnih in živahnih animacij. Trigonometrične in eksponentne funkcije so pri tem ključne. V tem vodiču si pridobil izkušnje z uporabo teh matematičnih konceptov v praksi.