Matematik i uttryck: Trigonometriska och exponentiella koncept

Matematik spelar en grundläggande roll i den digitala världen och framför allt inom videoredigering med After Effects (AE) öppnar den helt nya möjligheter för dig. I den här guiden kommer du att lära dig hur du kan använda trigonometriska och exponentiella funktioner i AE som uttryck för att skapa fascinerande animationer. Ett särskilt spännande exempel kommer att vara rörelsen hos en fjäril, som visar hur fysiska simuleringar kan genomföras med hjälp av matematik.

Viktigaste insikter

• Trigonometriska funktioner som sinus och cosinus kan användas för att skapa förskjutna rörelser.
• Exponentiella funktioner används för att simulera dämpningseffekter.
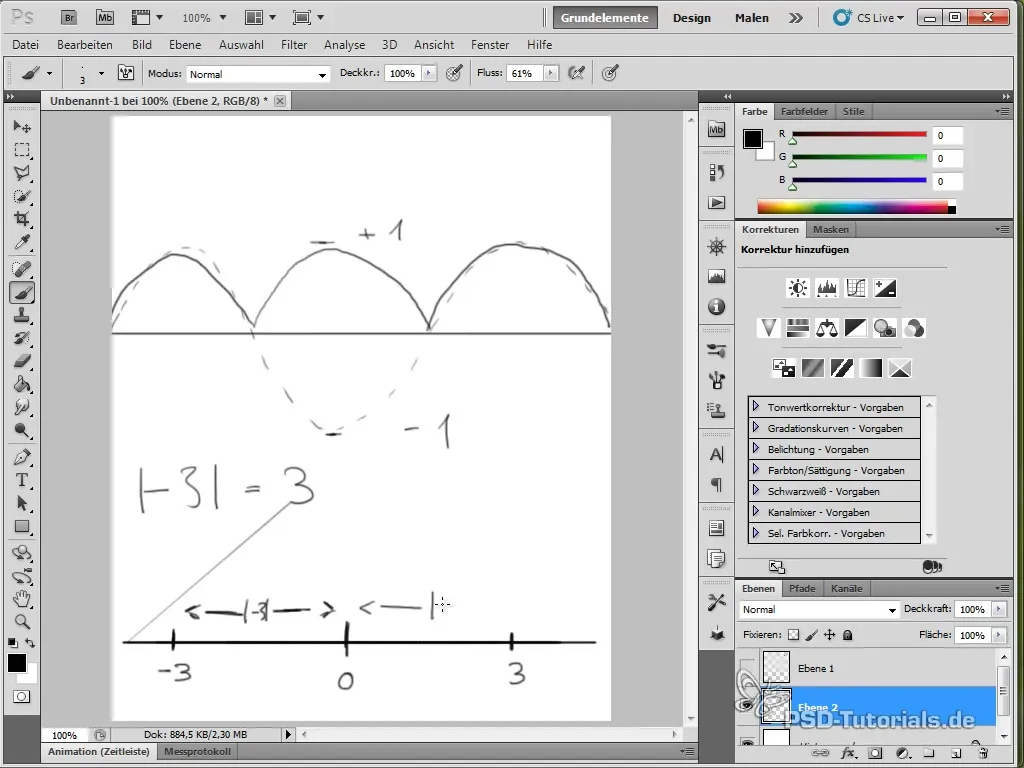
• Användning av absolutvärden i funktioner kan hjälpa till att uppnå vissa animations effekter.

Steg-för-steg-guide

Sätta fjärilen i rörelse

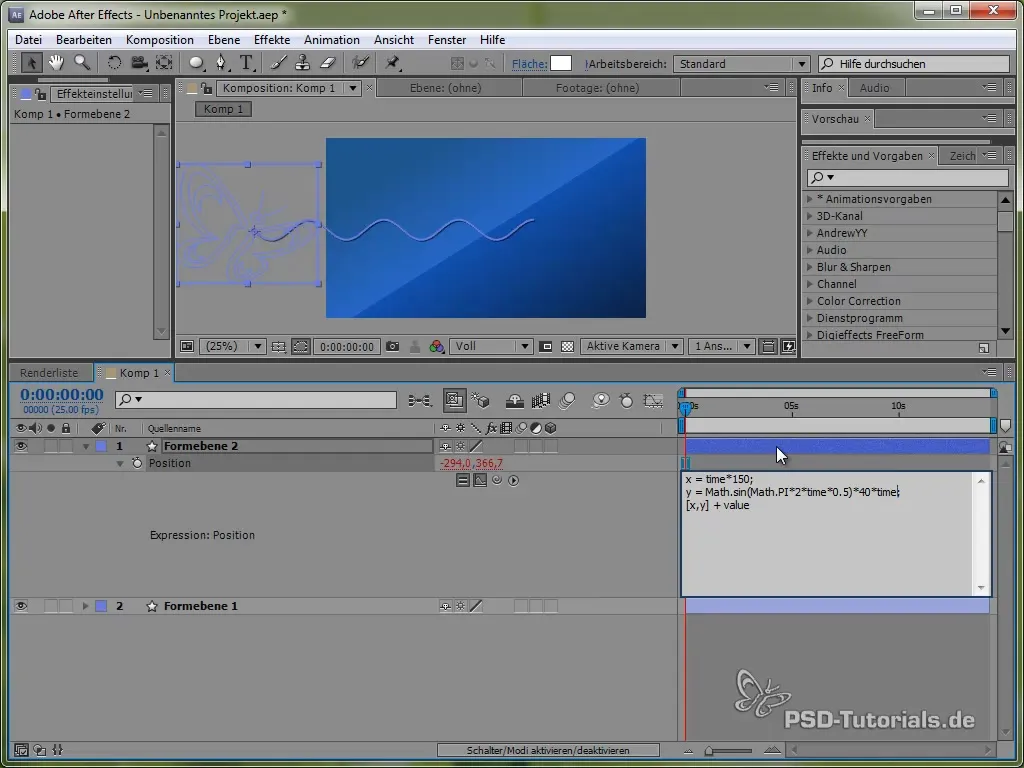
För att sätta vår fjäril i rörelse måste du först animera den så att den rör sig i en våg. Denna vågrörelse kan enkelt realiseras med hjälp av uttryck.

Börja med att öppna fjärilens position genom att trycka på "P" tangenten. Sätt sedan ett uttryck för positionen genom att hålla ned ALT-tangenten och klicka på klockan.

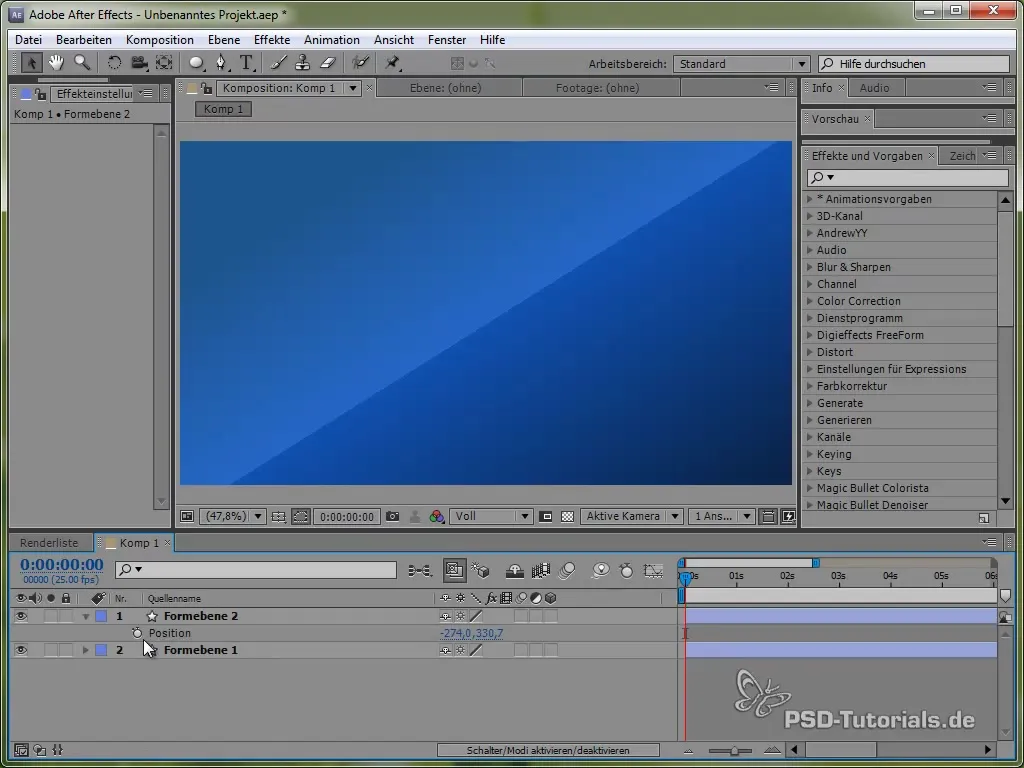
För detta använder vi först tidsvariabeln time, multiplicerat med ett värde som anger hastigheten på rörelsen. Till exempel:

value[0] + time * 150

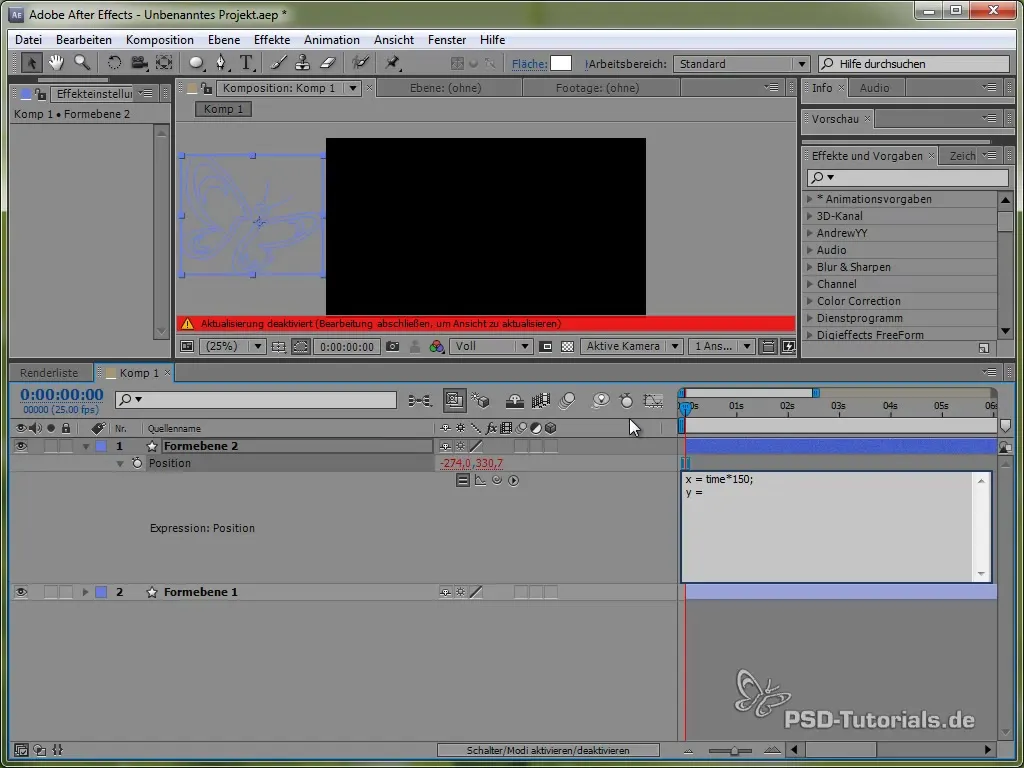
Denna kod gör att fjärilen rör sig konstant 150 pixlar per sekund i X-riktning. För Y-riktningen kommer vi att använda en sinusfunktion som skapar fjärilens vertikala rörelse och får den att "vagga" mellan vissa värden.

Tillämpa sinusfunktionen

Y-rörelsen definieras av följande uttryck:

value[1] + 40 * Math.sin(2 * Math.PI * time)

Här sätter Math.sin() sinusfunktionen i verket. Den varierar mellan -1 och 1 och multipliceras med 40, vilket innebär att fjärilen svävar mellan -40 och 40 pixlar i Y-riktning.

Visualisera rörelsegrafiken

För att bättre visualisera denna rörelse kan du aktivera grafikfönstret i After Effects. Detta visar svängningarna av sinusvärdet tydligare.

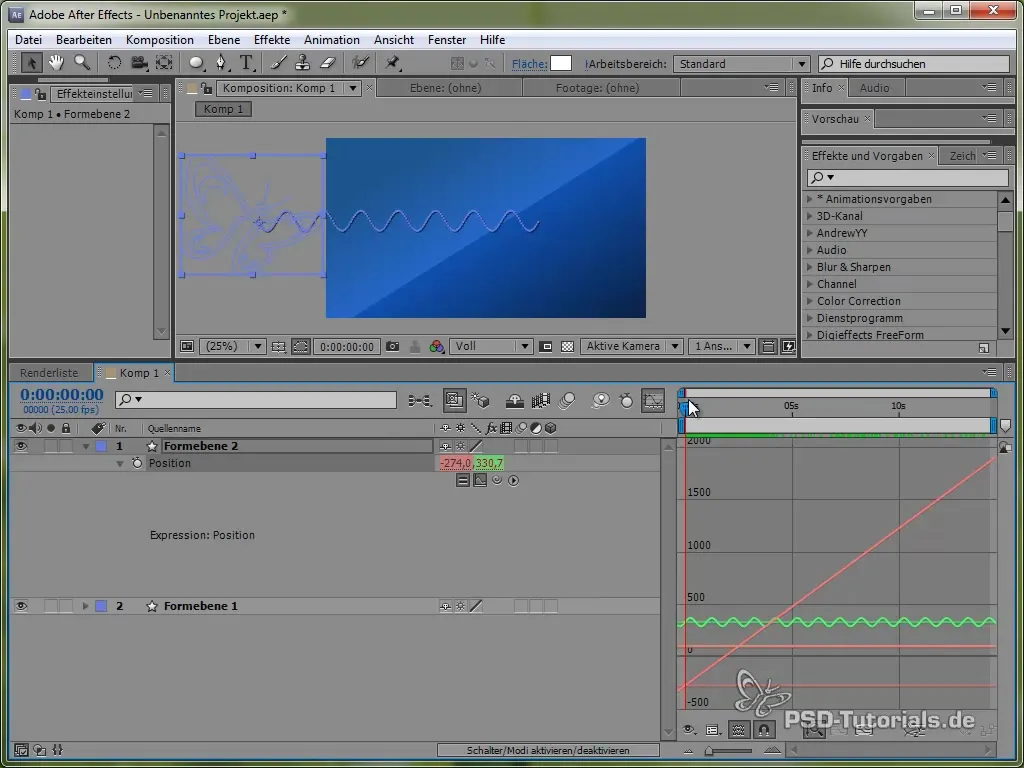
Det syns att signalen oscillerar och rör sig över skärmen.

Variera amplitud och frekvens

Nu kan du justera amplituden för att skapa olika starka svängningar. Om du till exempel vill öka amplituden över tid kan du använda följande:

40 * (time * 10) * Math.sin(2 * Math.PI * time)

Detta kommer att få amplituden att öka med tiden, vilket innebär att fjärilen svajar 40 pixlar efter en sekund, 80 pixlar efter två sekunder och så vidare.

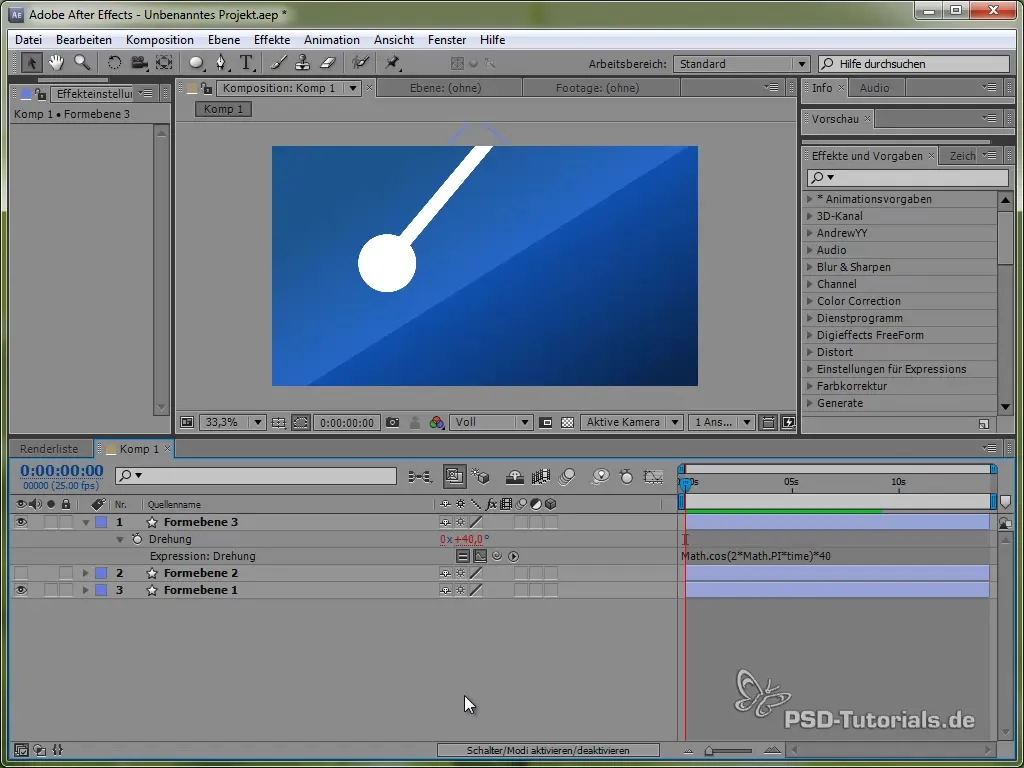
Skapa en pendel

För att fördjupa förståelsen av olika fysiska simuleringar riktar vi nu in oss på att skapa en pendel. Rita först en tunn stav och lägg till en ellips i änden av den.

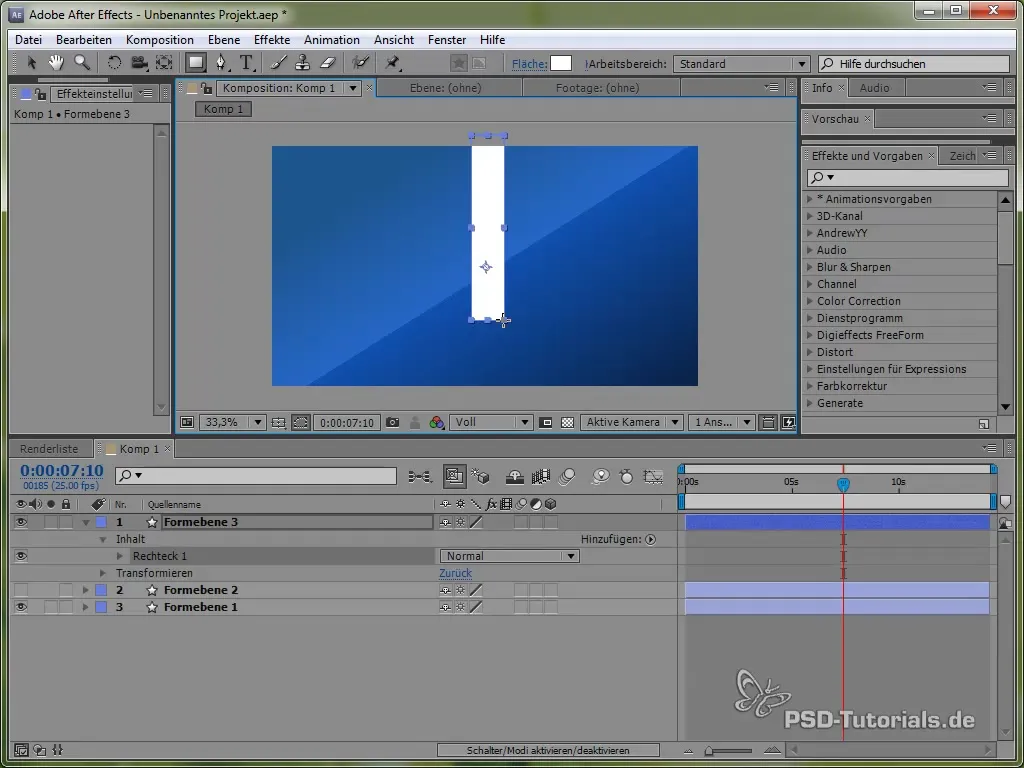
Placera ankarpunkten längst upp på pendeln så att den kan svänga. Detta görs med verktyget för ankarpunkten.

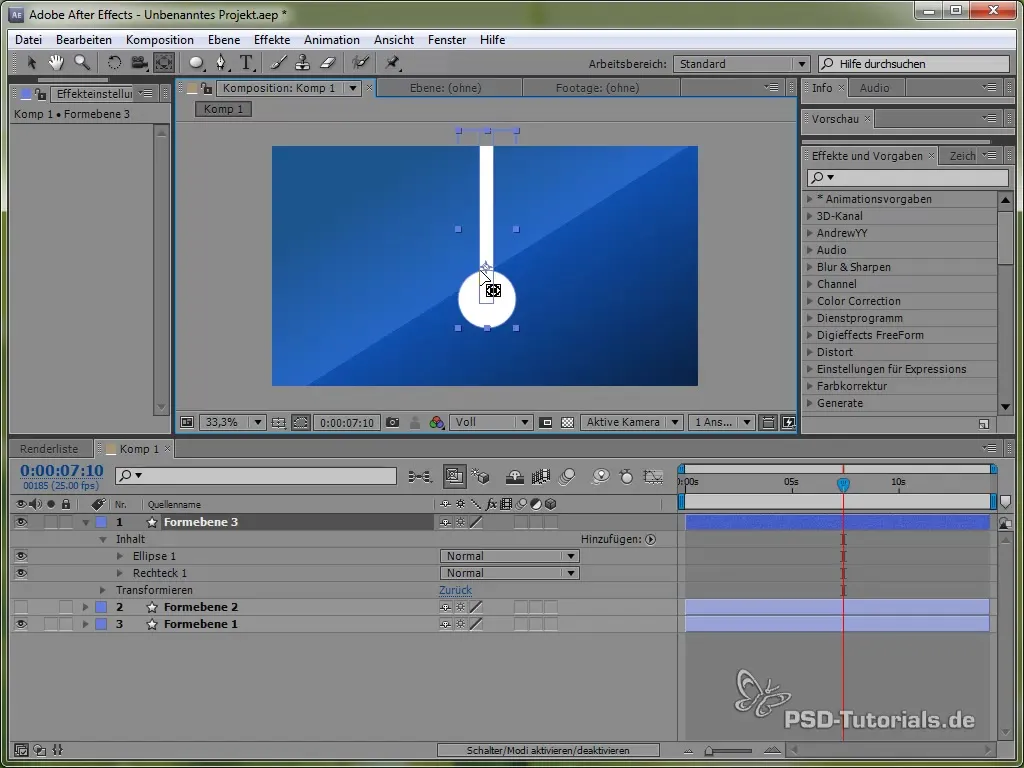
Sätt sedan in uttrycket:

value + 40 * Math.cos(2 * Math.PI * time)

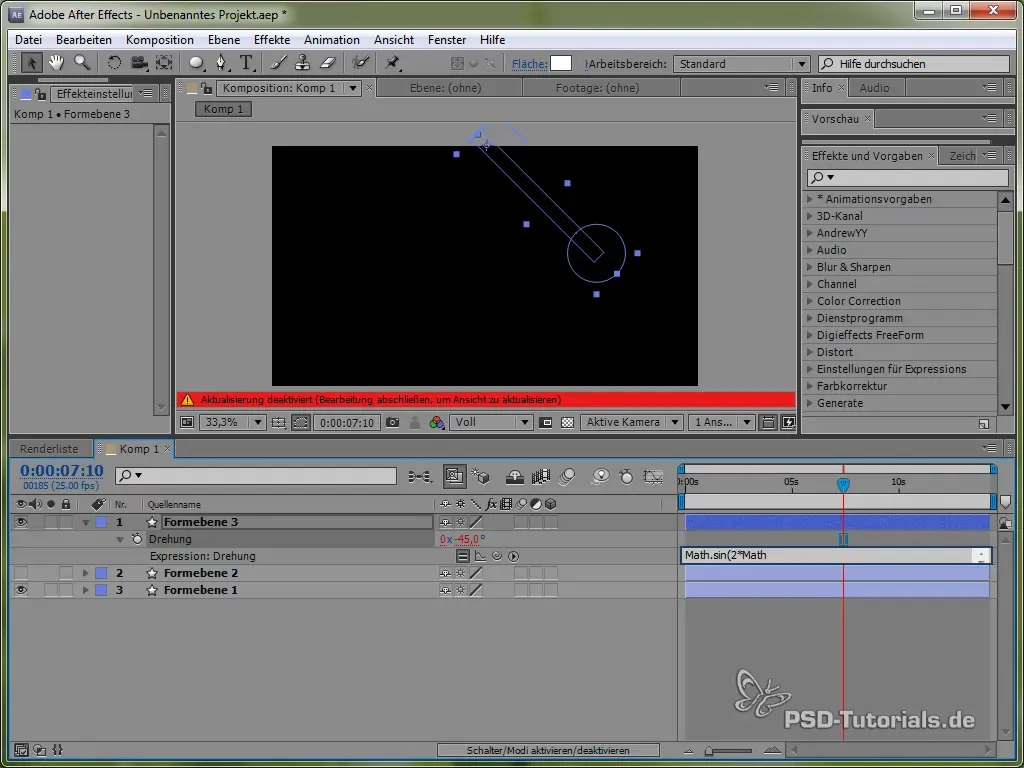
Genom cosinus påbörjar vi svängningsprocessen från en positiv punkt, vilket är realistiskt eftersom pendeln börjar svänga ovanifrån.

Infoga dämpningseffekter

För att integrera dämpning i svängningen använder vi den exponentiella funktionen. Detta gör svängningen mer realistisk eftersom den är stark i början och sedan avtar.

Ett exempel på kod kan se ut så här:

40 * Math.cos(2 * Math.PI * time) / Math.exp(time)

Här säkerställer divisionen genom den exponentiella funktionen en långsam dämpning.

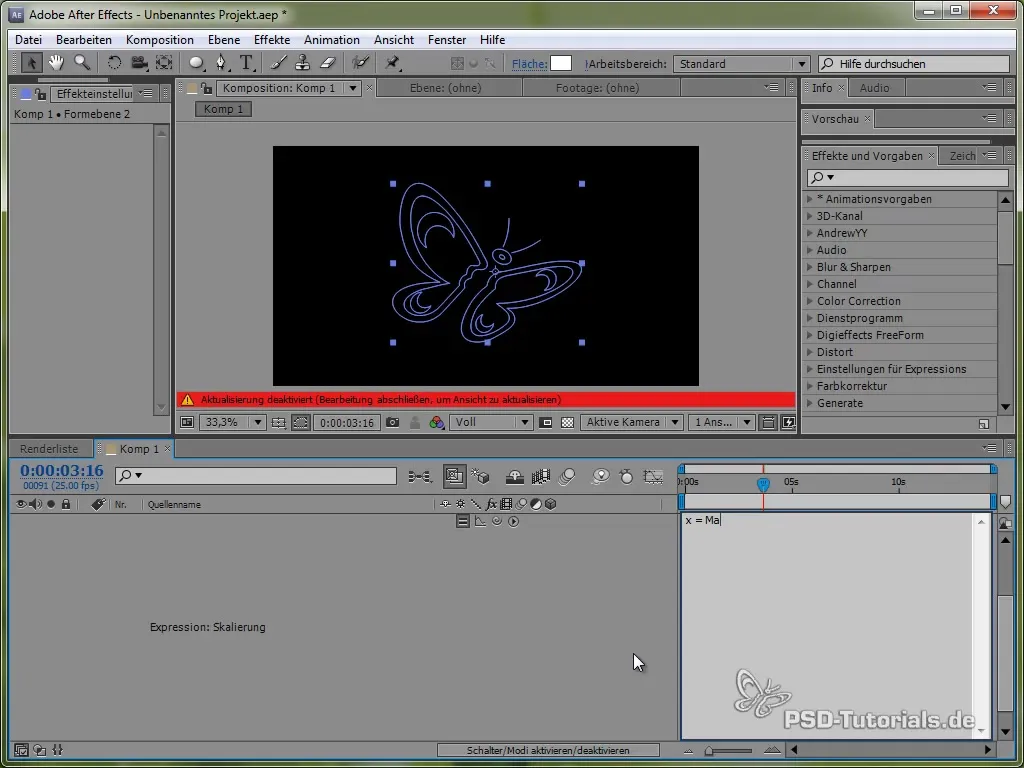
Lägg till squash och stretch

För livligare animationer kan du också lägga till squash and stretch-effekten. Du kan göra detta genom att skala fjärilen.

Du gör detta genom att tillämpa ett uttryck på skalan som kan tillämpas på både x- och y-värden genom att använda en sinus- eller cosinusfunktion.

Avslutande tankar

Det är tydligt att med rätt tillämpning av trigonometriska och exponentiella funktioner kan mycket realistiska och intressanta animationer skapas. Du har lärt dig hur man får en fjäril att flyga, hur man får en pendel att svänga och hur man arbetar med effekter som squash och stretch.

Sammanfattning - Matematik i Uttryck: Trigonometriska & Exponentiella Funktioner

Matematik i kontexten av uttryck i After Effects öppnar möjligheten att skapa kreativa och livliga animationer. Trigonometriska och exponentiella funktioner är därvid essentiella. I denna guide har du fått erfarenhet av att använda dessa matematiska koncept i praktiken.