Perusasiat muuttujista ja muistista ohjelmoinnissa

Kukin tietokone toimii itse asiassa vain hyvin yksinkertaisella, mutta perustavanlaatuisen tärkeällä rakenteella: tiedot tallennetaan 1:den ja 0:den muodossa. Mutta mitä oikein tapahtuu kulissien takana, kun käytät näitä 1:siä ja 0:ia? Tässä oppaassa tutustut muuttujien taustoihin ja käsitteeseen työmuistissa. Muuttujat ovat ratkaisevia tietojen tallentamiseksi tilapäisesti ja niiden käsittelemiseksi. Sukelletaan asiaan!

Tärkeimmät havainnot

• Muuttujat ovat olennaisia komponentteja, jotka mahdollistavat arvojen tallentamisen työmuistiin.
• Tietokonejärjestelmässä käsittelet tavuja ja bittejä, joissa yksi tavu koostuu 8 bitistä.
• Bitien arvo kasvaa eksponentiaalisesti, mikä on erittäin tärkeää ohjelmoinnissa ja tietojenkäsittelyssä.

Muuttujien perusteet

Ymmärtääksemme muuttujien toimintaa, meidän on ensin selvitettävä, mitä tarkalleen ottaen muutuja on. Ohjelmoinnissa muuttuja on paikkamerkki arvoille, joita voidaan muuttaa ohjelman suorituksen aikana. Ne mahdollistavat tietojen tilapäisen tallentamisen ja myöhemmin niihin pääsyn. Tämä tallennus tapahtuu työmuistissa, jota kutsutaan myös RAM:iksi (satunnaakses muistiksi).

Työmuistin merkitys

Työmuisti on haihtuva muisti, jossa tiedot ja ohjelmat tallennetaan niiden suorittamisen aikana. Kaikki, mitä teet tietokoneella, tapahtuu työmuistissa. Joten kun julistat muuttujan ja määrität sille arvon, tämä tieto tallennetaan työmuistiin, kunnes ohjelma lopetetaan tai muuttuja ylikirjoitetaan.

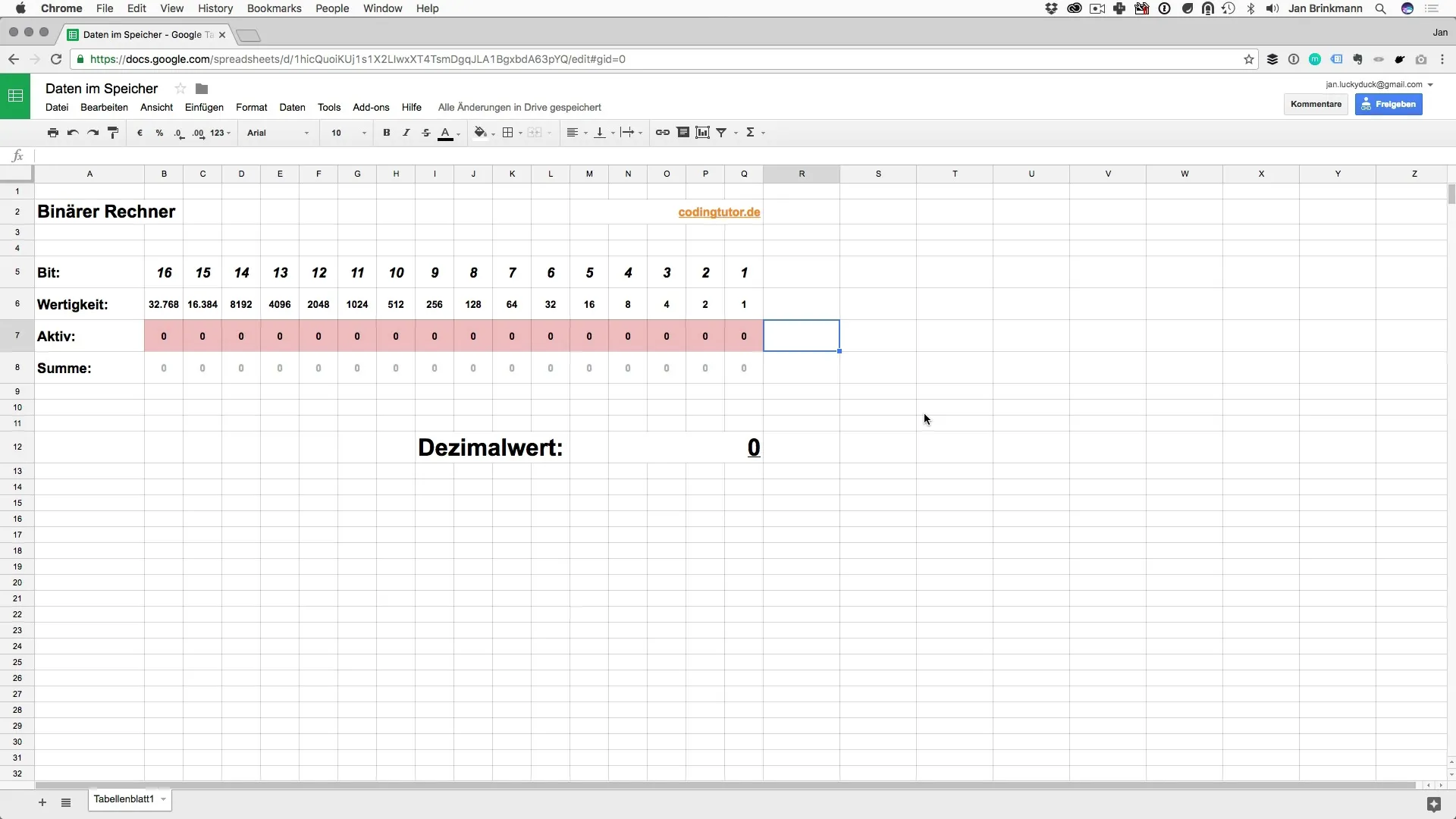
Ymmärrä bitit ja tavut

Keskusulkoilu tietojenkäsittelyssä on tavu. Tavu koostuu 8 bitistä. Jokainen bitti voi joko olla arvo 0 tai 1. Näiden bittien binaarinen yhteistyö palvelee tietojen tallentamista. Jokaisella bitillä on tietty sijainti ja siten tietty arvo. Nämä arvot ovat seuraavat:

• Bitti 1: 1
• Bitti 2: 2
• Bitti 3: 4
• Bitti 4: 8
• ja niin edelleen...

tämä rakenne muistuttaa kymmenjärjestelmää, jossa jokainen paikka edustaa 10:n potenssia. Binaarijärjestelmässä puolestaan arvo kaksinkertaistuu. Esimerkiksi, jos aktivoit neljännen bitin, yhdistelet arvot saadaksesi kymmenjärjestelmän arvon.

Binaarijärjestelmä käytännössä

Selkeyttääksesi käsitettä, otetaan esimerkki, jossa lisäät erilaisia bittejä. Kun vain bitti 1 on aktiivinen, se edustaa arvoa 1. Jos bitti 3 aktivoidaan myös, lisäät 4, jolloin saat arvoksi 5. Tämä voidaan yksinkertaisesti havainnollistaa binaarisella esityksellä.

Tämä tarkoittaa, että voit aktivoitujen bittien yhdistelmällä esittää monia erilaisia kymmenjärjestelmän arvoja. Esimerkiksi: jos bitti 5 on aktiivinen (32) ja bitti 3 (4) ja bitti 1 (1), yhdistelet näitä arvoja ja saat 37. Tämän tyyppistä laskentaa kutsutaan binaariseksi yhteenlaskuksi.

Kymmenjärjestelmästä binaariseen arvoon

Tärkeä käsite ohjelmoinnissa on kymmenjärjestelmän arvojen muuntaminen binaarisiin arvoihin. Jokainen aktivoitu bitti lisätään kokonaisarvoon. Jos aktivoit esimerkiksi bittin 5 (32) ja bittin 3 (4), yhdistelet arvot ja saat 36. Binaarinen arvo 36 olisi silloin 100100.

Arvojen skaalaus

Tietokoneen arvojen esittämisen rajat saavutetaan, kun tarkastelet järjestelmäsi kapasiteettia. Tyypillinen tietokone voi nykyään usein toimia 64-bittisissä arkkitehtuureissa. Tämä tarkoittaa, että sinulla on 2^64 mahdollista yhdistelmää, joka mahdollistaa äärimmäisen suurten kymmenjärjestelmän arvojen esittämisen. Periaate kuitenkin pysyy muuttumattomana ja on tärkeä ohjelmoinnille.

Yhteenveto – Muuttujat ja työmuisti: Ohjelmoinnin perusteet

Tässä oppaassa olet tutustunut muuttujien ja niiden rooliin työmuistissa. Ymmärrät nyt bitin ja tavun merkityksen ja miten niitä käytetään arvojen esittämiseen. Näiden käsitteiden ymmärtäminen on ratkaisevan tärkeää matkallasi ohjelmointiin.