Rekursi adalah istilah fundamental dalam ilmu komputer dan memainkan peran penting dalam menangani masalah yang kompleks. Jika kamu pernah berhadapan dengan tugas yang mengacu pada prinsip yang sama, pasti kamu sudah mendengar tentang rekursi. Baik dalam perhitungan matematis maupun dalam struktur data, kemungkinannya sangat beragam. Dalam panduan ini, kita akan membahas secara khusus tentang pembuatan metode rekursif dalam Java untuk menghitung faktorial dari sebuah angka. Mari kita pahami langkah demi langkah bagaimana kamu dapat mengimplementasikan rekursi dengan efektif.
Poin-poin penting
- Rekursi adalah pemanggilan yang merujuk pada dirinya sendiri
- Setiap metode rekursif memerlukan kondisi penghentian
- Dalam perhitungan faktorial, masalah dibagi menjadi sub-masalah yang lebih kecil
Panduan Langkah-demi-Langkah untuk Mengimplementasikan Perhitungan Faktorial
Untuk membuat metode rekursif, kita mulai dengan dasar-dasarnya. Faktorial dari sebuah angka n (n!) adalah hasil kali dari semua angka bulat positif hingga n. Misalnya, faktorial dari 3 (3!) sama dengan 1 × 2 × 3 = 6.
1. Definisi Metode
Pertama-tama, kita perlu mendefinisikan metode yang menghitung faktorial. Kita menggunakan tipe pengembalian long untuk menangani angka yang lebih besar secara efisien.
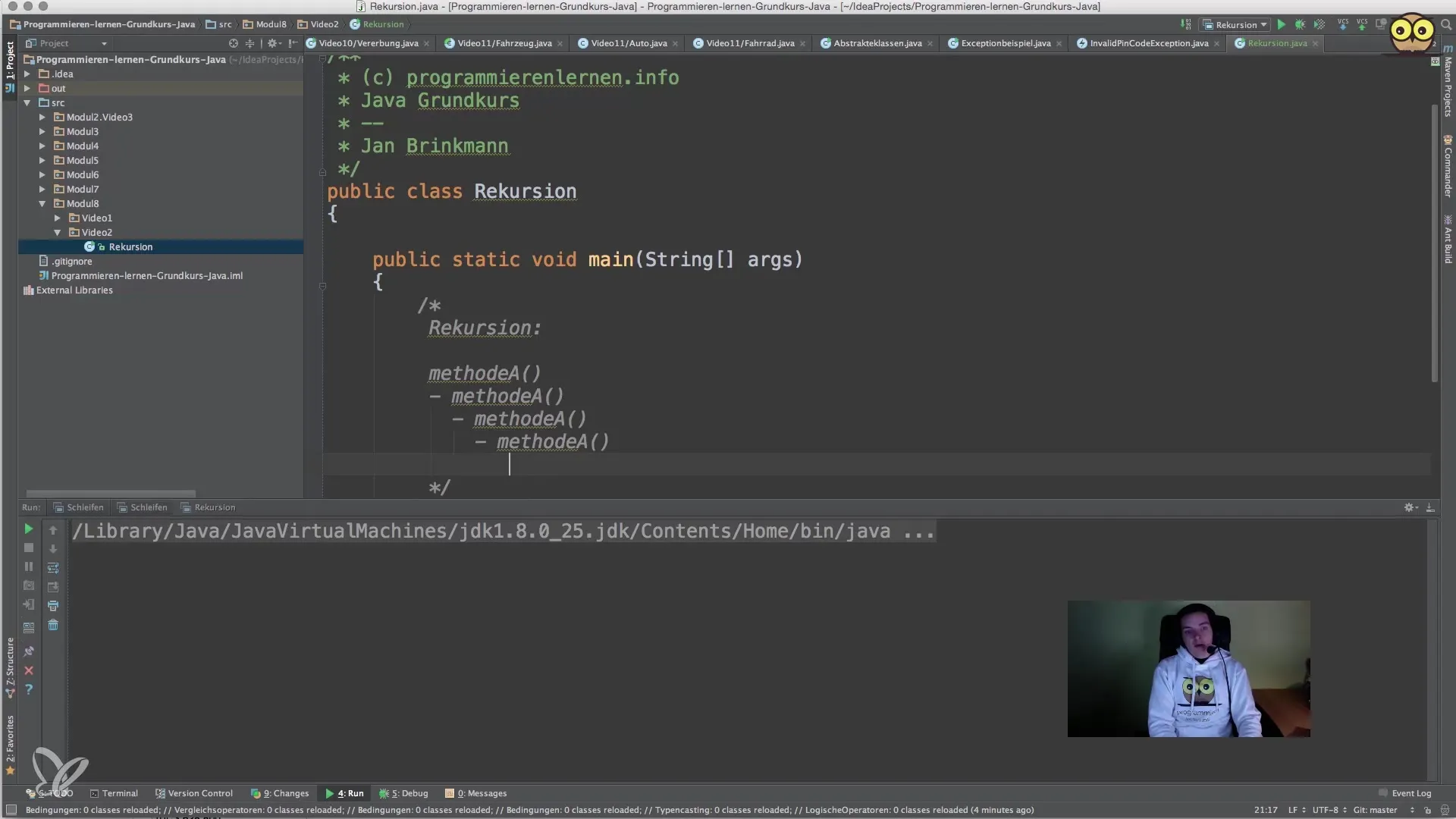
Metode ini dideklarasikan sebagai statis, karena kita ingin memanggilnya dari metode utama.
Di sini, kamu telah meletakkan kerangka untuk metode kamu.
2. Kondisi Penghentian
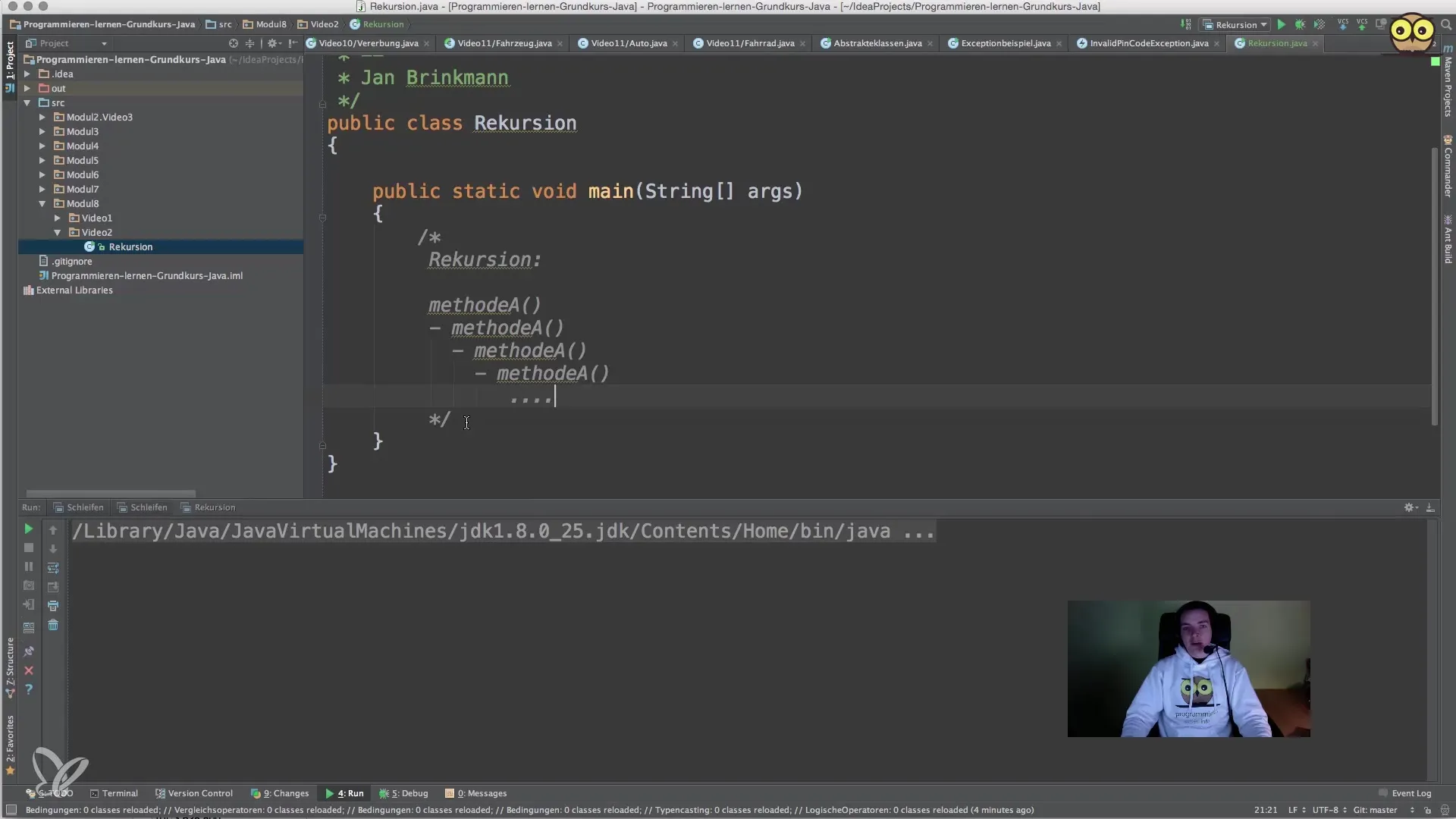
Elemen kunci dari sebuah metode rekursif adalah kondisi penghentian. Ini harus memastikan bahwa rekursi tidak berjalan tanpa henti. Dalam perhitungan faktorial, kondisi penghentian adalah kita menghitung faktorial dari 0 atau 1, yang keduanya menghasilkan nilai 1.
Baris ini memberi tahu metode bahwa ia dapat menyelesaikan perhitungan segera jika sudah mencapai 0 atau 1.
3. Pemanggilan Rekursif
Sekarang kita masuk ke bagian utama dari metode kita – pemanggilan rekursif. Di sini, kita memanggil metode kita di dalam metode itu sendiri, tetapi dengan nilai yang telah dikurangi.
Ini berarti kita mengalikan angka saat ini dengan faktorial dari angka yang telah dikurangi satu.
4. Kode Lengkap
Sekarang kita gabungkan semua bagian dan melihat seperti apa metode kita.
5. Memanggil Metode
Kita sekarang memanggil metode kita di dalam metode utama untuk menguji apakah semuanya berfungsi dengan baik.
6. Menguji dan Memeriksa Hasil
Jika kamu menjalankan program sekarang, itu harus mengeluarkan faktorial dari 3 adalah: 6.
Penting untuk memeriksa hasilnya untuk memastikan semuanya berfungsi dengan benar.
7. Menggunakan Debugger
Saya merekomendasikan kamu untuk menggunakan debugger untuk lebih memahami proses rekursi. Menjalani langkah demi langkah akan menunjukkan kepada kamu bagaimana nilai ditransfer melalui beberapa pemanggilan.
Kamu dapat mengamati bagaimana metode tersebut dipanggil secara rekursif, yang akan membantumu untuk memahami logika dasar dari rekursi.
Ringkasan – Rekursi dalam Java – Metode Efisien dengan Pemanggilan Diri
Penggunaan rekursi bisa menjadi tantangan di awal, tetapi menawarkan cara yang efektif untuk menyelesaikan masalah yang kompleks. Dalam panduan ini, kamu telah belajar bagaimana mengimplementasikan metode rekursif untuk menghitung faktorial dalam Java. Kita telah membahas konsep penting seperti kondisi penghentian dan logika rekursif.
Pertanyaan yang Sering Diajukan
Apa itu rekursi?Rekursi adalah metode di mana sebuah fungsi memanggil dirinya sendiri untuk menyelesaikan suatu masalah.
Kenapa kondisi penghentian diperlukan?Kondisi penghentian mencegah fungsi dipanggil tanpa henti sehingga dapat menyebabkan tumpukan overflow.
Bagaimana cara menghitung faktorial dari sebuah angka?Faktorial n (n!) adalah hasil kali dari semua angka bulat positif dari 1 hingga n.


