Matematika išraiškose: Trigonometriniai ir eksponentiniai konceptai

Matematika skaitmeninėje pasaulyje vaidina fundamentalią rolę, o ypač vaizdo redagavime su After Effects (AE) ji atveria visiškai naujas galimybes. Šiame pamoke tau bus mokoma, kaip trigonometrijos ir eksponentinės funkcijas AE naudoti kaip išraiškas, kad sukurtum įspūdingas animacijas. Ypatingas pavyzdys bus drugelio judėjimas, kuris parodys, kaip fizinės simulacijos gali būti įgyvendintos naudojant matematiką.

Svarbiausi įžvalgos

• Trigonometrinės funkcijos, tokios kaip sinusas ir kosinusas, gali būti naudojamos sukurti nukrypusių judesių efektus.
• Eksponentinės funkcijos yra naudojamos simuliuoti slopinimo efektus.
• Absoliučių vertių naudojimas funkcijose gali padėti pasiekti tam tikrus animacijos efektus.

Žingsnis po žingsnio vadovas

Drugelį judėti

Norint, kad mūsų drugelis judėtų, pirmiausia reikia jį animuoti taip, kad jis judėtų banga. Šią bangos judėjimą galima lengvai realizuoti naudojant išraiškas.

Pradėk, paspaudęs klavišą „P“, kad atidarytum drugelio poziciją. Tada nustatyk išraišką pozicijai, paspaudęs ALT klavišą ir spustelėdamas laikrodį.

Tam pirmiausia panaudosime laiką kaip kintamąjį, padaugintą iš vertės, kuri nustato judėjimo greitį. Pavyzdžiui:

value[0] + time * 150

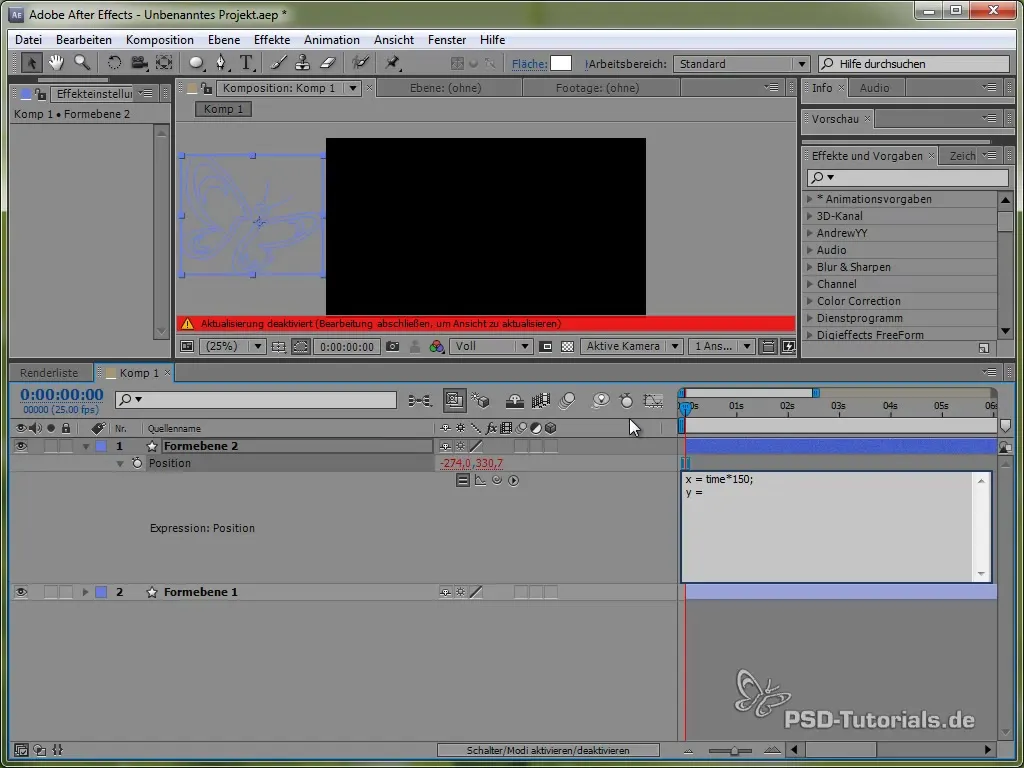
Šis kodas lemia, kad drugelis X kryptimi judės nuolat 150 pikselių per sekundę. Y kryptimi mes naudosime sinusinę funkciją, kuri sukurs vertikalų drugelio judėjimą ir leis jam „svyruoti“ tarp tam tikrų verčių.

Sinusinės funkcijos taikymas

Y judėjimas bus apibrėžtas šia išraiška:

value[1] + 40 * Math.sin(2 * Math.PI * time)

Čia Math.sin() interpretuoja sinusinę funkciją. Ji svyruoja tarp -1 ir 1, o tai dauginama iš 40, kas reiškia, kad drugelis Y kryptimi svyruos tarp -40 ir 40 pikselių.

Judėjimo grafiką vizualizuoti

Kad šį judėjimą geriau vizualizuotum, gali įjungti grafikų langą After Effects. Tai aiškiau parodys sinusinės vertės svyravimus.

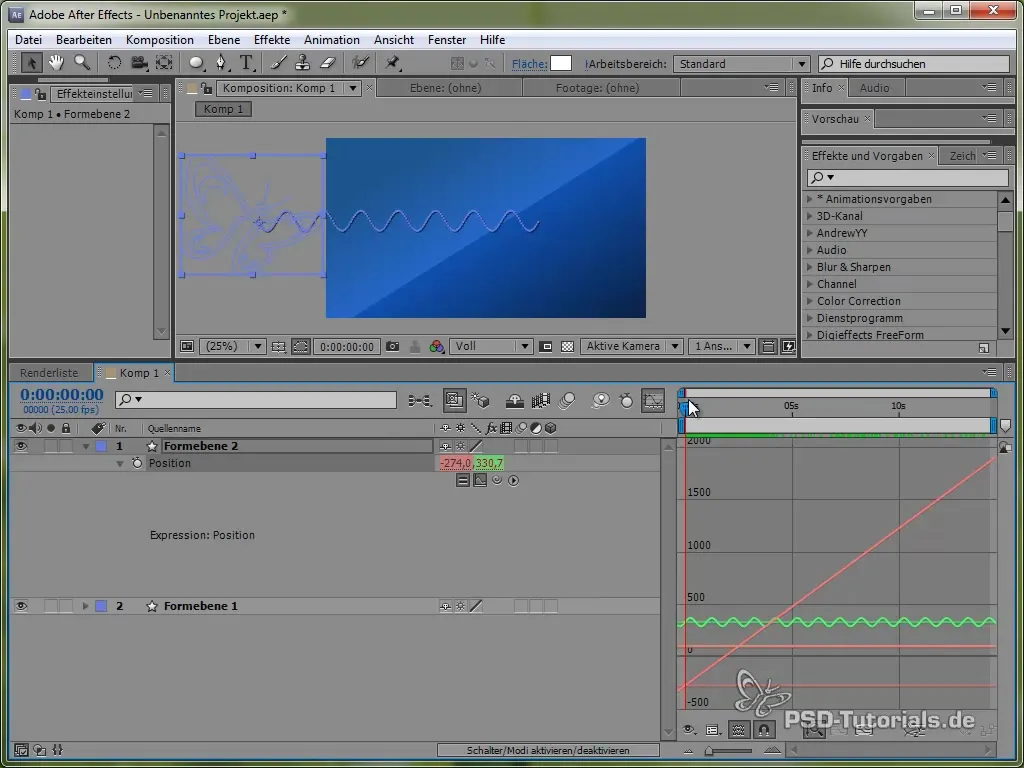
Matyti, kad signalas osciluoja ir juda per ekraną.

Amplitudę ir dažnį keisti

Dabar gali keisti amplitudę, kad sukurtum skirtingus svyravimo stiprumus. Pavyzdžiui, jei nori didinti amplitudę laikui bėgant, gali naudoti šį kodą:

40 * (time * 10) * Math.sin(2 * Math.PI * time)

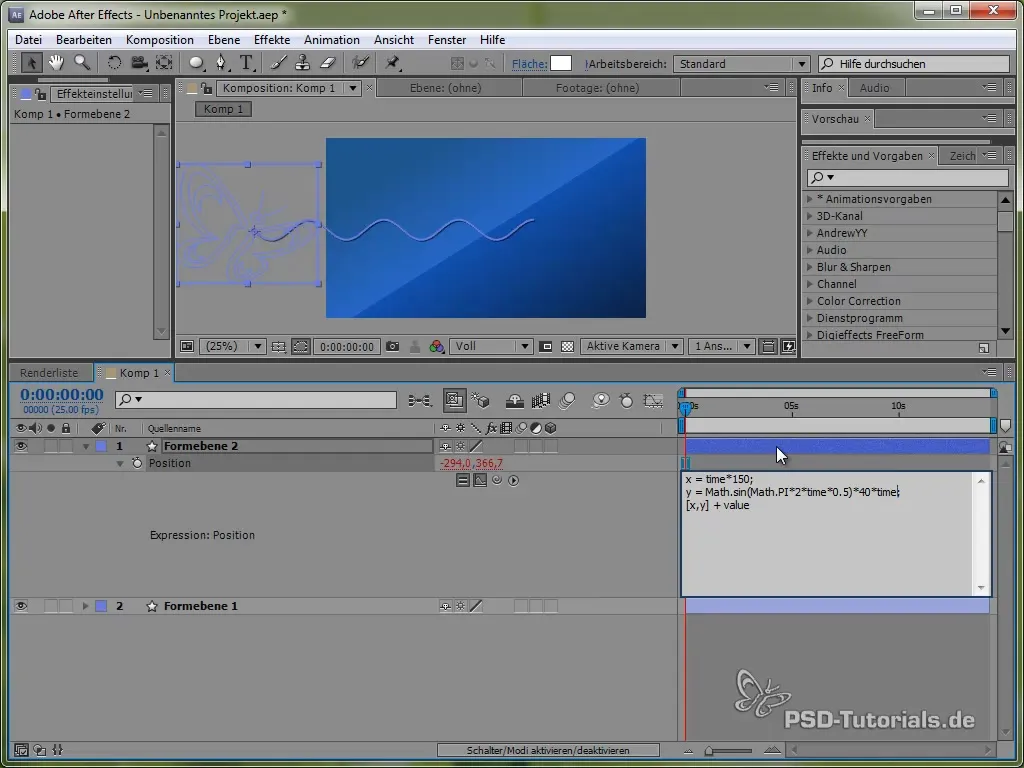
Taip amplitudė kils laikui bėgant, todėl drugelis po vienos sekundės svyruos 40 pikselių, po dviejų sekundžių – 80 pikselių ir taip toliau.

Kūrimo svyruoklė

Norėdami gilinti supratimą apie įvairias fizines simuliacijas, dabar pereikime prie svyruoklės kūrimo. Pirmiausia nupiešk ploną lazdelę ir prie jos galo pridėk elipsę.

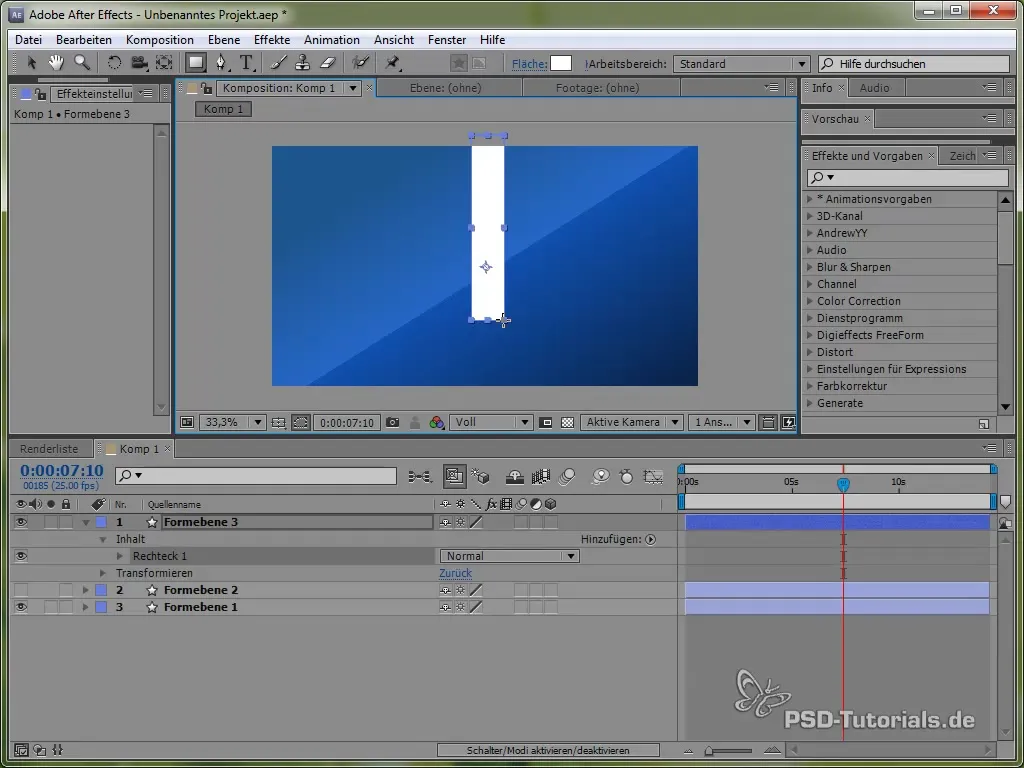
Pozicionuok ankerį viršuje svyruoklės, kad ji galėtų svyruoti. Tai atliks su ankerio įrankiu.

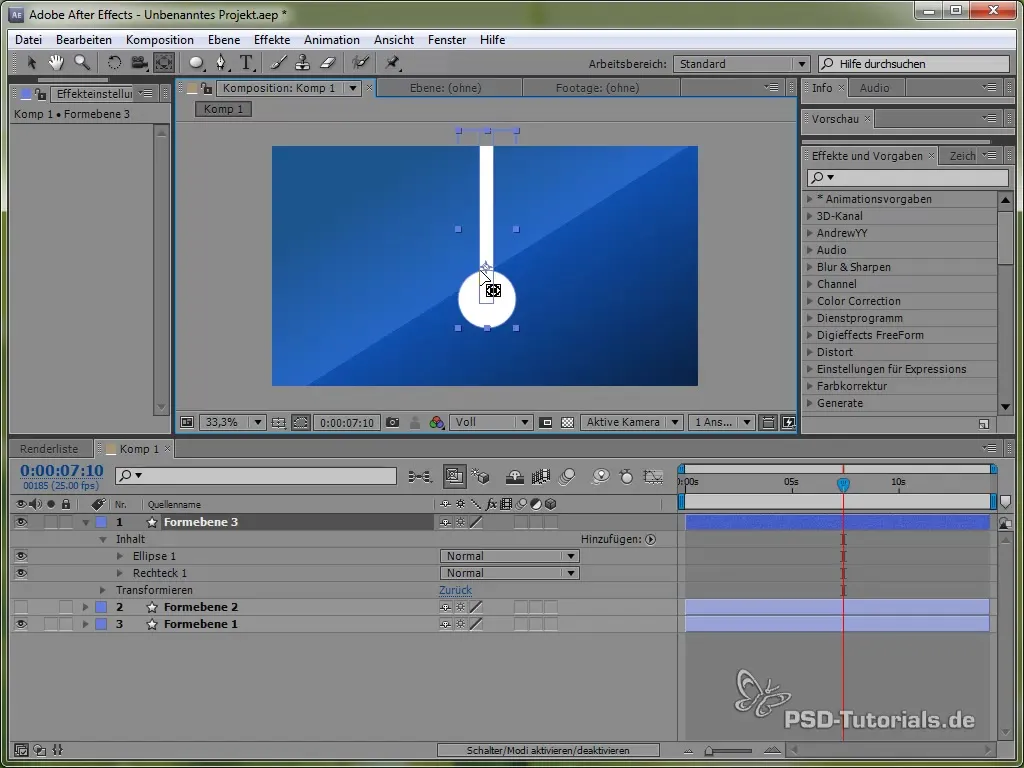
Tada nustatyk išraišką:

value + 40 * Math.cos(2 * Math.PI * time)

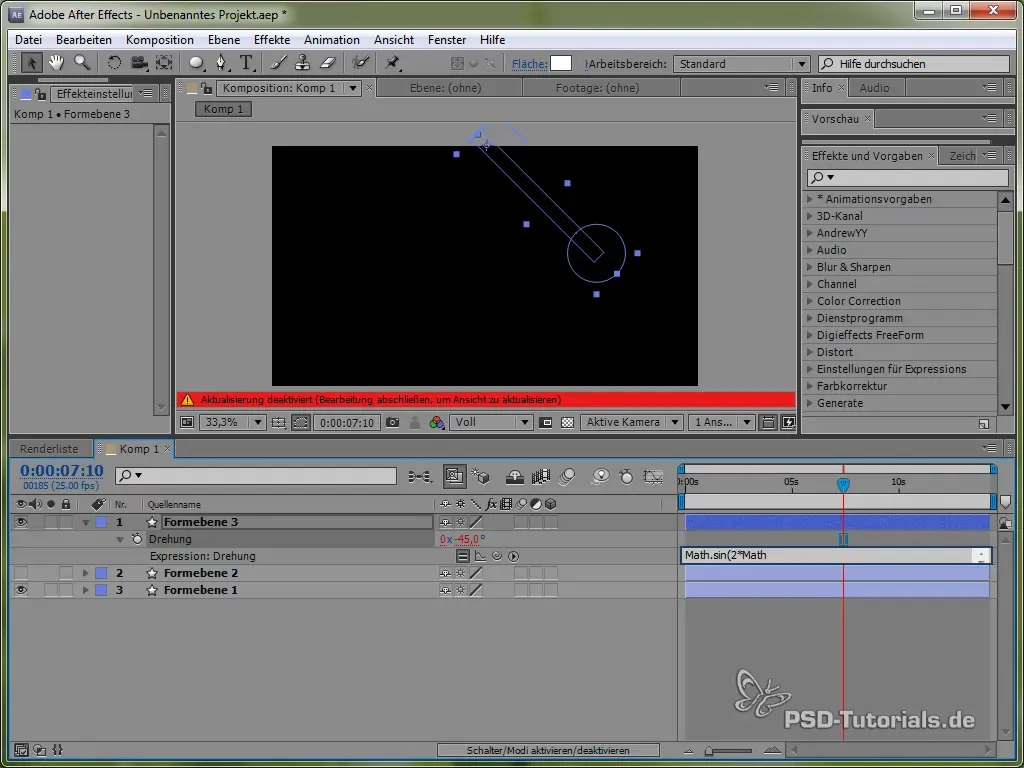
Paremtas kosinusine funkcija pradedame judesių procesą iš teigiamos vertės, kas yra realistiška, kadangi svyruoklė pradeda svyruoti iš viršaus.

Slopinimo efektų pridėjimas

Kad integruotum slopinimą į svyravimą, naudojame eksponentinę funkciją. Tai padaro svyravimą realesnį, kad pradžioje jis yra stiprus, o galų gale sumažėja.

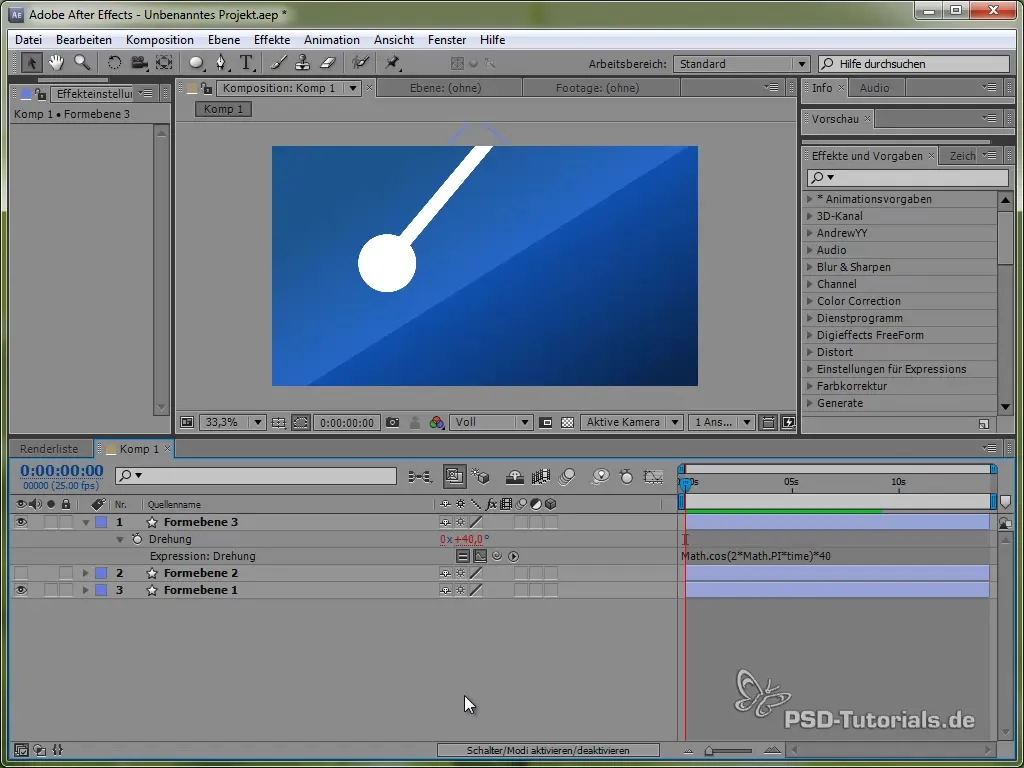
Pavyzdžio kodas galėtų atrodyti taip:

40 * Math.cos(2 * Math.PI * time) / Math.exp(time)

Čia dalybos su eksponentine funkcija būtų lėtas slopinimas.

Squash ir Stretch pridėjimas

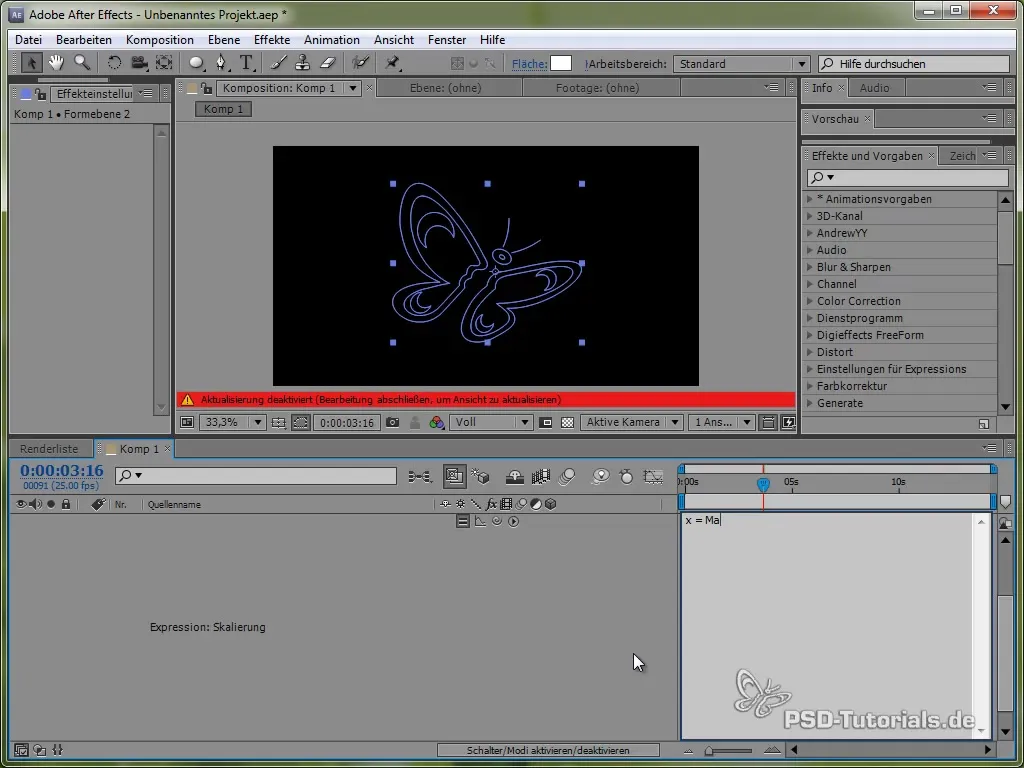
Norint gyvesnių animacijų, taip pat gali pridėti Squash and Stretch efektą. Tai gali būti pasiekta keičiant drugelio mastelį.

Tai padaroma taikant išraišką mastelio skalėje, kuri gali būti taikoma tiek x, tiek y vertėms, naudojant sinusinę ar kosinusinę funkciją.

Galutinės mintys

Matyti, kad tinkamai naudojant trigonometrines ir eksponentines funkcijas galima sukurti labai realistiškas ir įdomias animacijas. Tu išmokei, kaip leisti drugeliui skristi, kaip svyruoti svyruoklei ir kaip dirbti su efektais, tokiais kaip Squash ir Stretch.

Santrauka - Matematika Išraiškose: Trigonometrijos & Eksponentinės funkcijos

Matematika išraiškų kontekste After Effects atveria galimybes kurti kūrybingas ir gyvas animacijas. Trigonometrijos ir eksponentinės funkcijos yra esminės. Šioje pamokoje tu pasisėmei patirties, kaip naudoti šias matematikos koncepcijas praktikoje.