Matemática desempenha um papel fundamental no mundo digital e, especialmente na edição de vídeo com After Effects (AE), ela abre novas possibilidades para você. Neste tutorial, você aprenderá a usar funções trigonométricas e exponenciais no AE como expressões para criar animações fascinantes. Um exemplo particularmente empolgante será o movimento de uma borboleta, que mostrará como simulações físicas podem ser implementadas com a ajuda da matemática.
Principais conclusões
- Funções trigonométricas como seno e cosseno podem ser usadas para gerar movimentos oscilantes.
- Funções exponenciais são usadas para simular efeitos de amortecimento.
- O uso de valores absolutos em funções pode ajudar a alcançar certos efeitos de animação.
Guia passo a passo
Pôr a borboleta em movimento
Para colocar nossa borboleta em movimento, primeiro você deve animá-la de forma que ela se mova em uma onda. Esse movimento ondulatório pode ser realizado sem grandes esforços através das expressões.
Comece abrindo a posição da borboleta pressionando a tecla “P”. Em seguida, defina uma expressão para a posição, pressionando a tecla ALT e clicando no relógio.
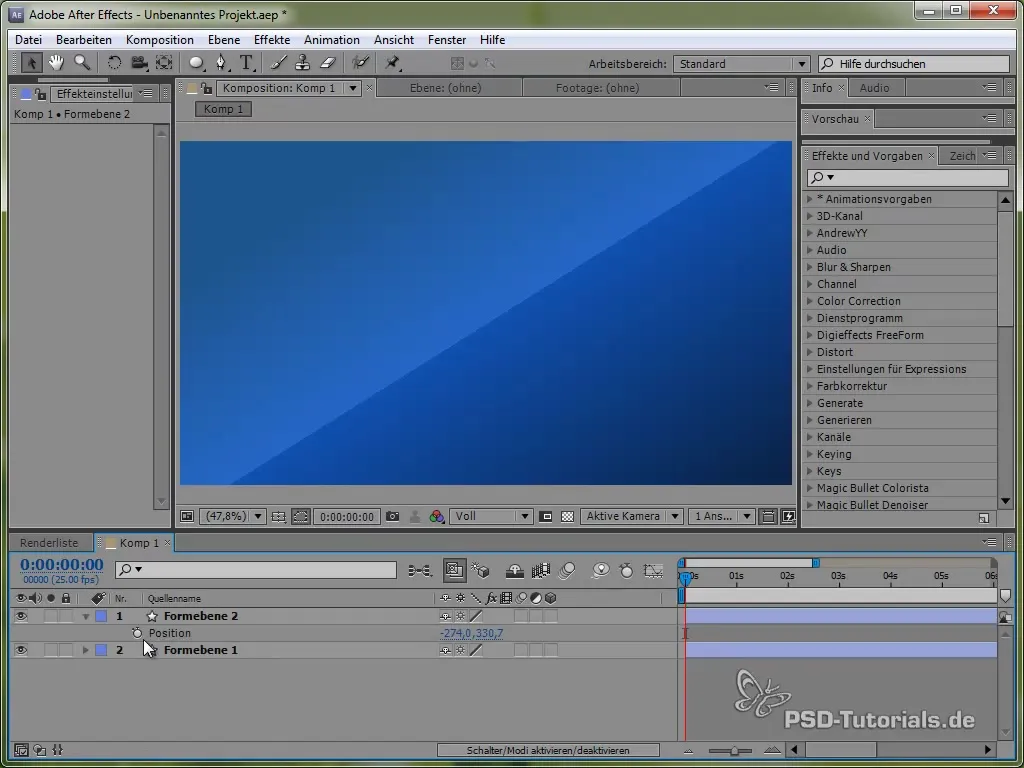
Para isso, primeiro usamos a variável de tempo time, multiplicada por um valor que determina a velocidade do movimento. Por exemplo:
value[0] + time * 150
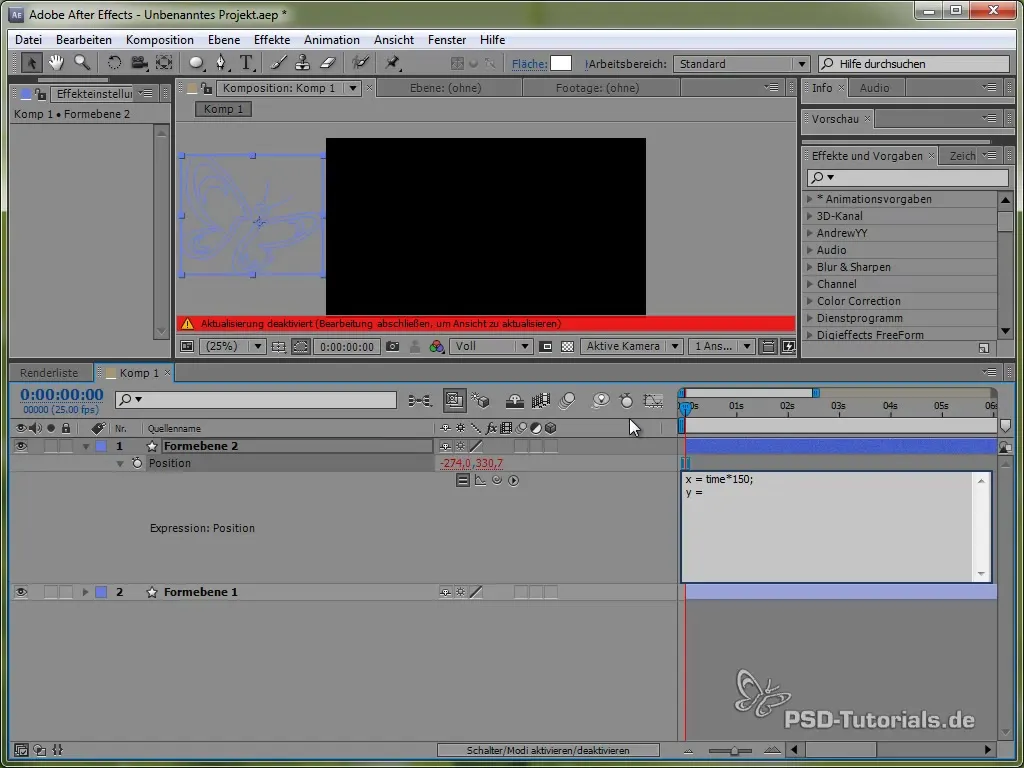
Esse código faz com que a borboleta se mova constantemente 150 pixels por segundo na direção X. Para a direção Y, usaremos uma função seno que cria o movimento vertical da borboleta e faz com que ela "balance" entre certos valores.
Aplicação da função seno
O movimento Y é definido pela seguinte expressão:
value[1] + 40 * Math.sin(2 * Math.PI * time)
A função Math.sin() implementa a função seno. Ela varia entre -1 e 1 e é multiplicada por 40, o que significa que a borboleta oscilará na direção Y entre -40 e 40 pixels.
Visualizando a gráfica do movimento
Para visualizar melhor esse movimento, você pode ativar a janela de gráficos no After Effects. Isso mostrará as oscilações do valor seno de forma mais clara.
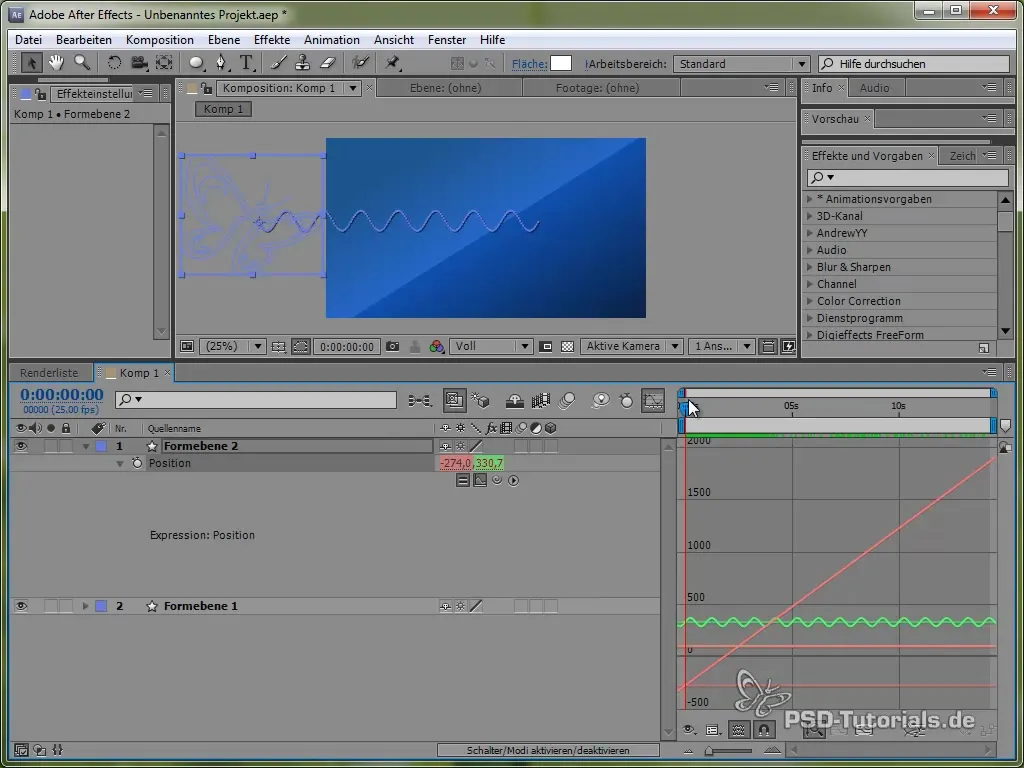
Pode-se ver que o sinal oscila e se move pela tela.
Variando a amplitude e a frequência
Agora você pode ajustar a amplitude para gerar oscilações de diferentes intensidades. Se você quiser aumentar a amplitude ao longo do tempo, pode usar o seguinte:
40 * (time * 10) * Math.sin(2 * Math.PI * time)
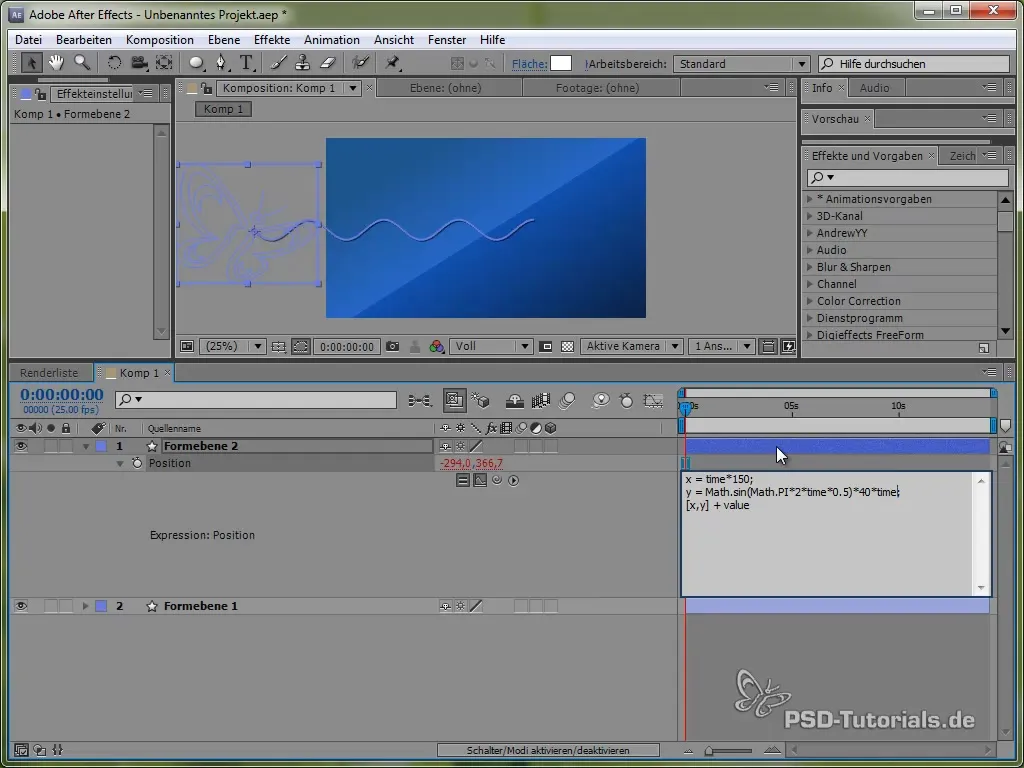
Com isso, a amplitude aumentará com o tempo, fazendo com que a borboleta oscile 40 pixels após um segundo, 80 pixels após dois segundos e assim por diante.
Criando um pêndulo
Para aprofundar o manuseio de diferentes simulações físicas, agora nos voltaremos para a criação de um pêndulo. Primeiro, desenhe um bastão fino e adicione uma elipse na sua extremidade.
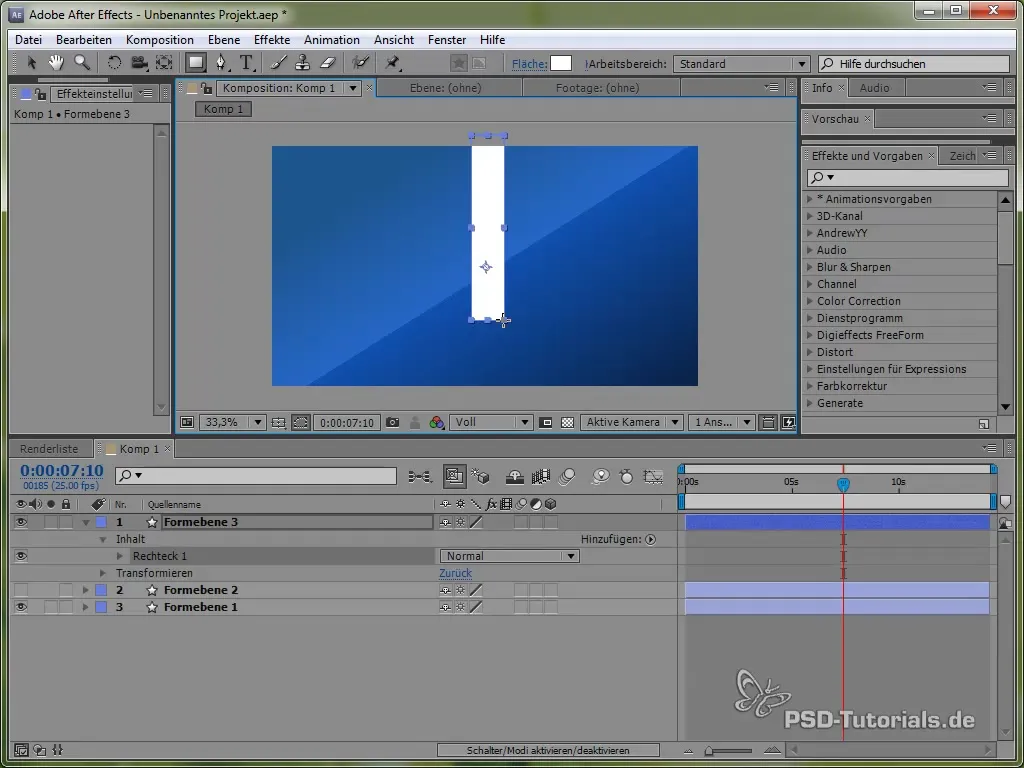
Posicione o ponto âncora na parte superior do pêndulo, para que ele possa oscilar. Isso é feito com a ferramenta de ponto âncora.
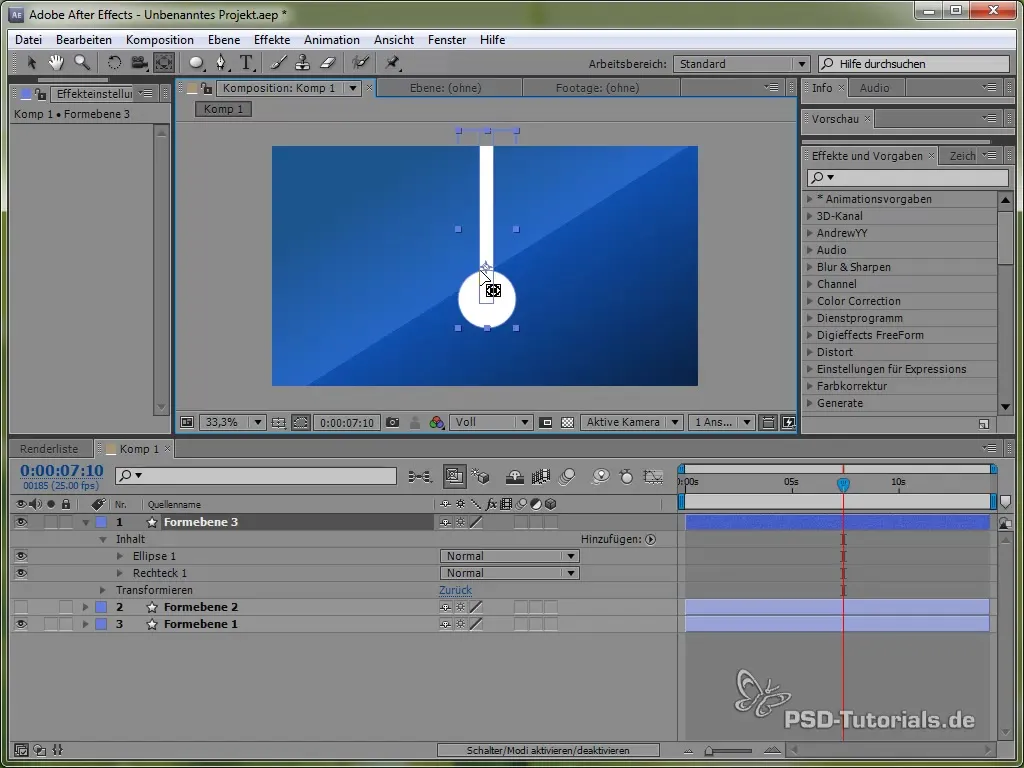
Em seguida, defina a expressão:
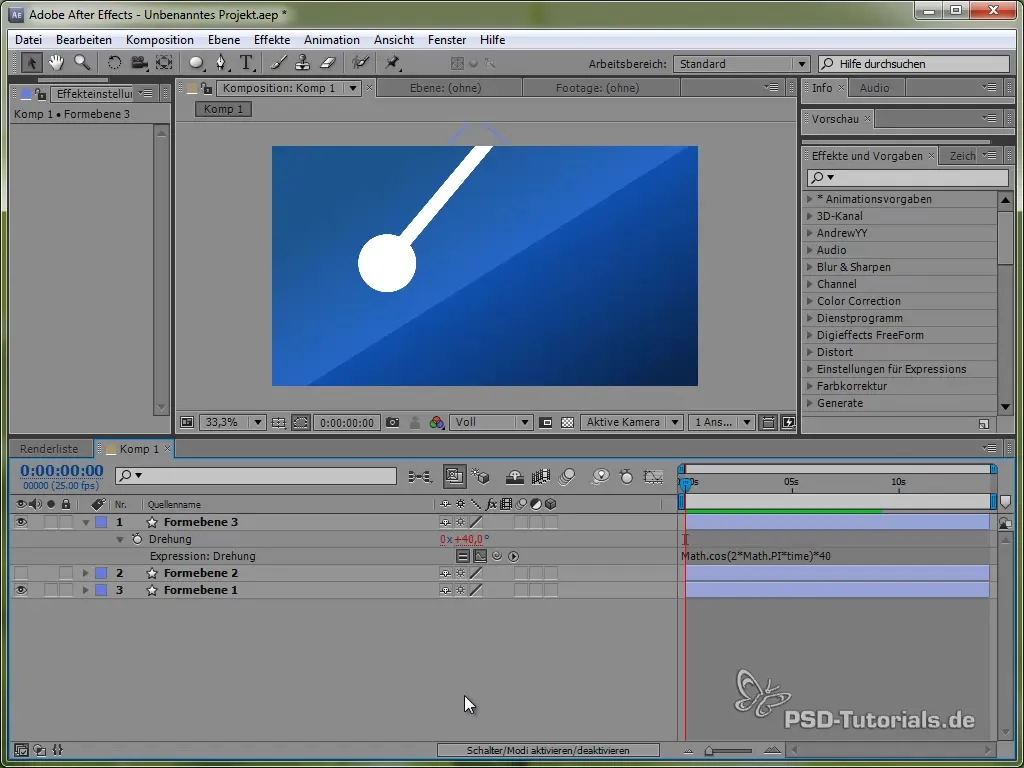
value + 40 * Math.cos(2 * Math.PI * time)
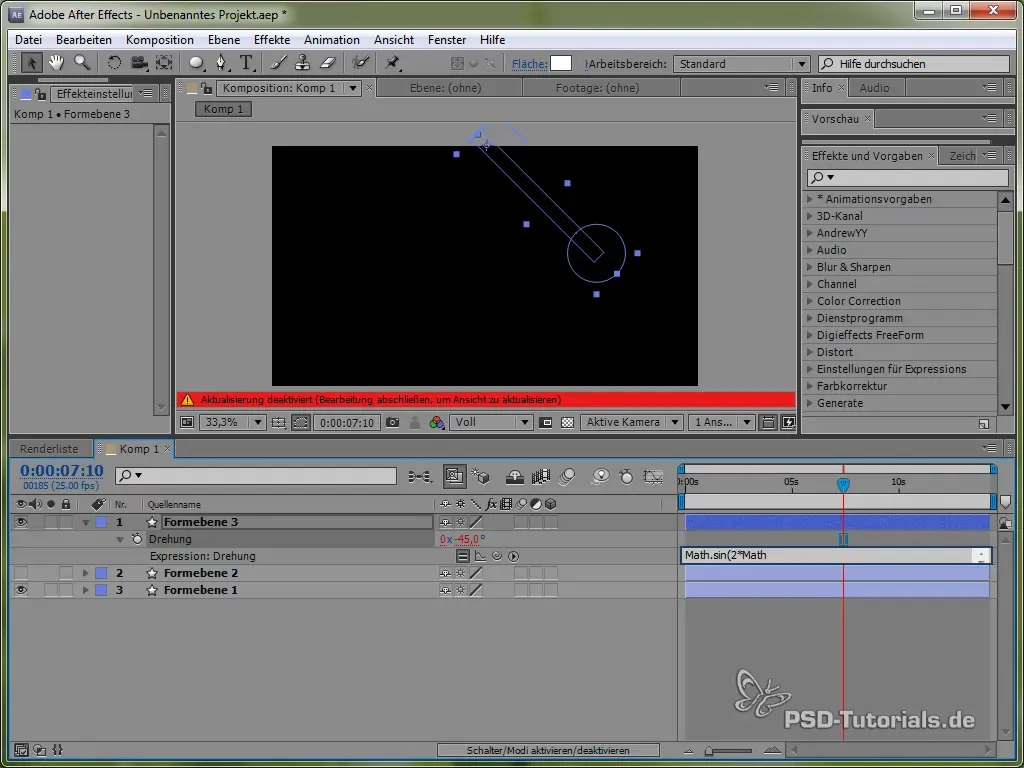
Com o cosseno, iniciamos o processo de oscilação a partir de um ponto positivo, o que é realista, pois o pêndulo começa a oscilar do topo.
Inserindo efeitos de amortecimento
Para integrar o amortecimento na oscilação, usamos a função exponencial. Isso torna a oscilação mais realista, pois é forte no início e diminui com o tempo.
Um exemplo de código pode ser:
40 * Math.cos(2 * Math.PI * time) / Math.exp(time)
Nisso, a divisão pela função exponencial causa um amortecimento lento.
Adicionando Squash e Stretch
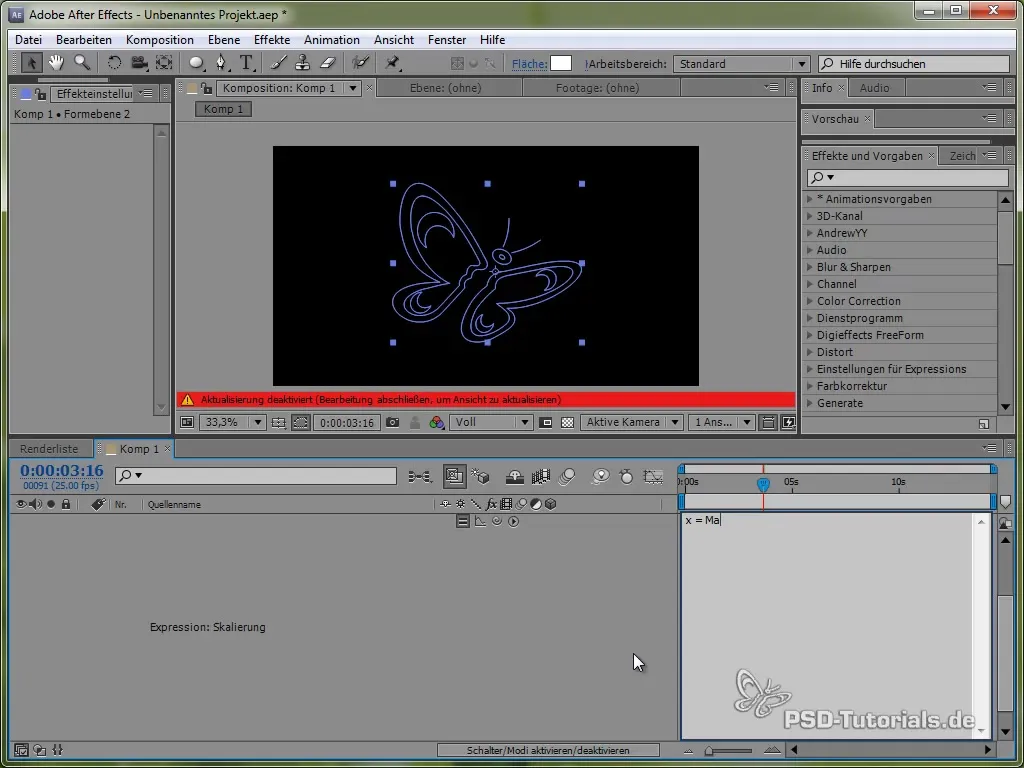
Para animações mais vibrantes, você também pode adicionar o efeito Squash and Stretch. Isso pode ser alcançado através da escalabilidade da borboleta.
Você faz isso aplicando uma expressão à escala de escala, que pode ser aplicada a valores de x e y, utilizando uma função seno ou cosseno.
Pensamentos finais
Pode-se ver que, com a aplicação correta de funções trigonométricas e exponenciais, animações bastante realistas e interessantes podem ser criadas. Você aprendeu a fazer uma borboleta voar, um pêndulo oscilar e como trabalhar com efeitos como Squash e Stretch.
Resumo - Matemática em Expressões: Funções Trigonométricas & Exponenciais
A matemática no contexto de expressões no After Effects abre a possibilidade de criar animações criativas e vibrantes. Funções trigonométricas e exponenciais são essenciais nesse processo. Neste tutorial, você adquiriu experiência na aplicação desses conceitos matemáticos na prática.
Perguntas Frequentes
Como coloco uma expressão no After Effects?Pressione a tecla ALT e clique no relógio ao lado da propriedade para a qual você deseja adicionar a expressão.
Qual é a diferença entre funções seno e cosseno?A função seno começa em 0, enquanto a função cosseno começa em 1. Isso afeta a forma como as animações iniciam.
Como posso criar efeitos de amortecimento?Você pode gerar efeitos de amortecimento inserindo funções exponenciais em suas expressões, que reduzem o movimento ao longo do tempo.


