Рекурсія є фундаментальним поняттям в інформатиці і відіграє вирішальну роль у вирішенні складних проблем. Якщо ти коли-небудь стикався з завданнями, де проблема знову звертається до того ж принципу, ти, мабуть, вже чув про рекурсію. Чи то в математичних обчисленнях, чи в структурі даних, можливості безмежні. У цьому посібнику ми говоримо зокрема про створення рекурсивного методу в Java для обчислення факторіалу числа. Давай зрозуміємо крок за кроком, як ти можеш ефективно використовувати рекурсію.
Основні висновки
- Рекурсія є самовідсилаючим викликом
- Кожен рекурсивний метод потребує умови завершення
- При обчисленні факторіалу проблема ділиться на менші підпроблеми
Покрокова інструкція з реалізації обчислення факторіалу
Щоб створити рекурсивний метод, почнемо з основ. Факторіал числа n (n!) є добутком усіх позитивних цілих чисел до n. Наприклад, факторіал 3 (3!) дорівнює 1 × 2 × 3 = 6.
1. Визначення методу
Перш ніж визначити метод, який обчислює факторіал, ми використаємо тип повернення long, щоб ефективно обробляти більші числа.
Метод буде оголошений статичним, оскільки ми хочемо викликати його з головного методу.
У цьому рядку ти вже заклав шаблон для свого методу.
2. Умова завершення
Важливим елементом рекурсивного методу є умова завершення. Вона повинна забезпечити, щоб рекурсія не тривала безкінечно. При обчисленні факторіалу умова завершення полягає в тому, що ми обчислюємо факторіал 0 або 1, які обидва дорівнюють 1.
Цей рядок повідомляє методу, що при 0 або 1 обчислення можна завершити відразу.
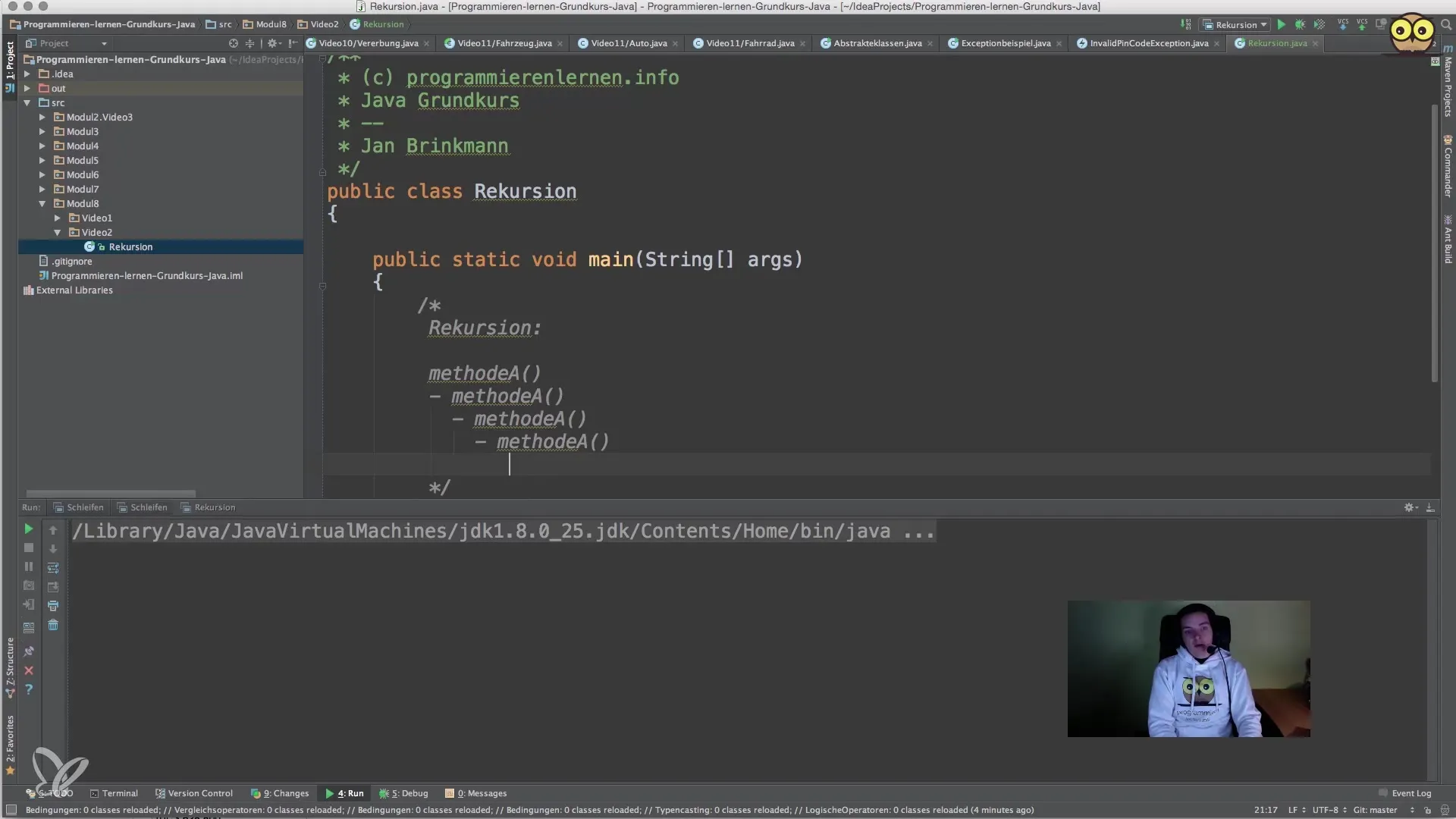
3. Рекурсивний виклик
Тепер йде основна частина нашого методу – рекурсивний виклик. Тут ми викликаємо наш метод всередині самого методу, але з зменшеним значенням.
Це означає, що ми множимо поточне число на факторіал числа, яке зменшено на одиницю.
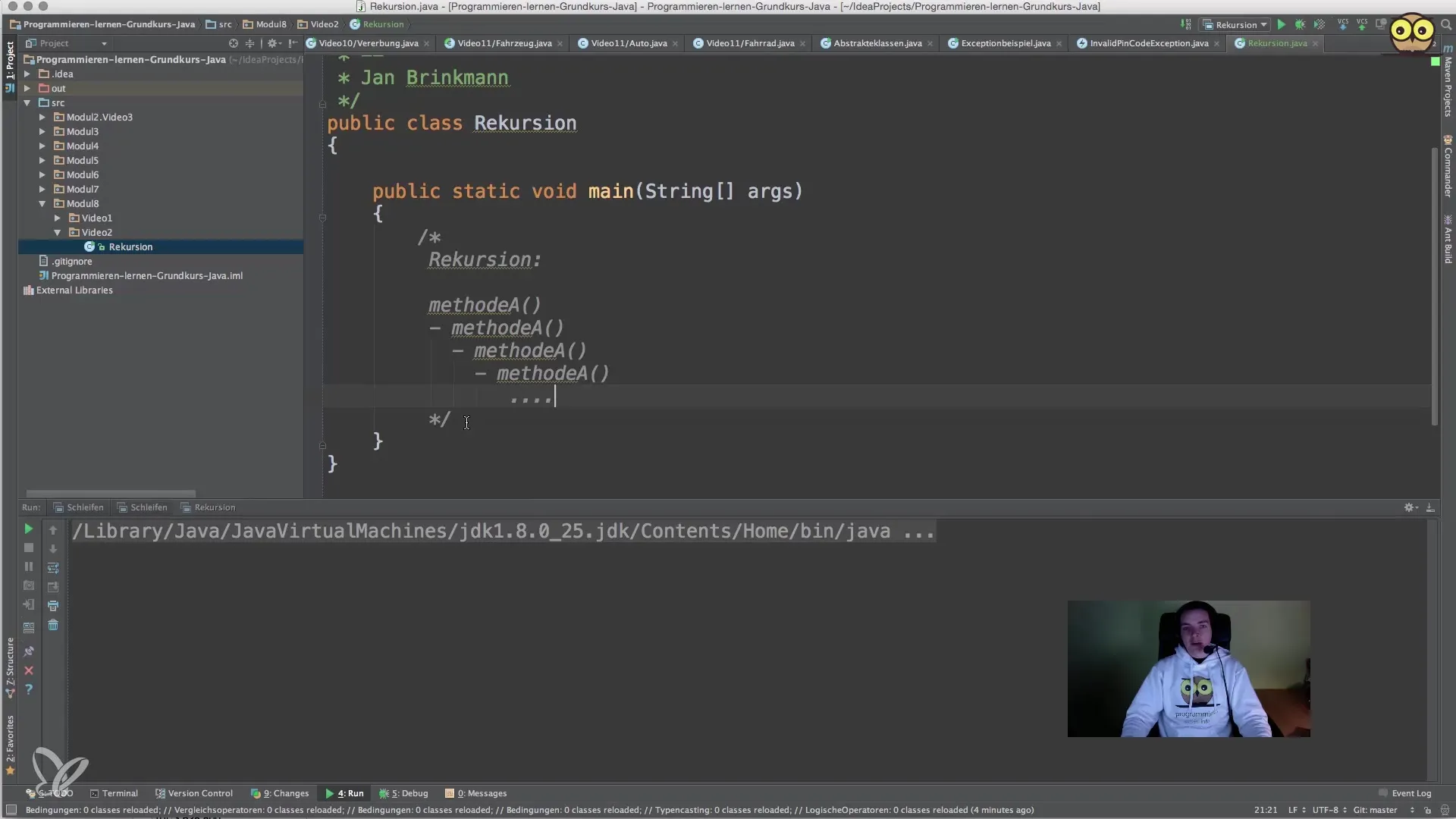
4. Повний код
Тепер зберемо всі частини разом і побачимо, як виглядає наш метод.
5. Виклик методу
Ми тепер викликаємо наш метод у головному методі, щоб перевірити, чи все працює.
6. Тестування та перевірка результатів
Коли ти зараз запустиш програму, вона повинна вивести факторіал 3: 6.
Важливо перевірити результат, щоб переконатися, що все працює правильно.
7. Використання дебагера
Рекомендую тобі використовувати дебагер, щоб краще зрозуміти процес рекурсії. Покрокове проходження покаже тобі, як значення передаються через кілька викликів.
Ти можеш спостерігати, як метод рекурсивно викликається, що допоможе тобі зрозуміти основну логіку рекурсії.
Підсумок – Рекурсія в Java – Ефективні методи з самовикликами
Використання рекурсії може спочатку бути складним, але пропонує ефективний спосіб вирішення складних проблем. У цьому посібнику ти дізнався, як реалізувати рекурсивний метод для обчислення факторіалу в Java. При цьому ми розглянули важливі концепції, такі як умова завершення та рекурсивна логіка.
Часто задавані питання
Що таке рекурсія?Рекурсія – це метод, при якому функція викликає саму себе для розв’язання проблеми.
Чому необхідна умова завершення?Умова завершення запобігає безкінечним викликам функції, що може призвести до переповнення стека.
Як обчислюється факторіал числа?Факторіал n (n!) є добутком усіх позитивних цілих чисел від 1 до n.


