Matematika v výrazech: Trigonometrické a exponenciální koncepty

Matematika hraje ve digitálním světě základní roli a zejména v editaci videa s After Effects (AE) ti otevírá zcela nové možnosti. V této příručce se naučíš, jak využívat trigonometické a exponenciální funkce v AE jako výrazy k vytváření fascinujících animací. Zvlášť vzrušujícím příkladem bude pohyb motýla, který ti ukáže, jak lze fyzikální simulace provádět pomocí matematiky.

Nejdůležitější poznatky

• Trigonometrické funkce jako sinus a kosinus mohou být použity k vytváření posunutých pohybů.
• Exponenciální funkce se používají k simulaci tlumících efektů.
• Použití absolutních hodnot v funkcích může pomoci dosáhnout určitých animačních efektů.

Pokyny krok za krokem

Oživění motýla

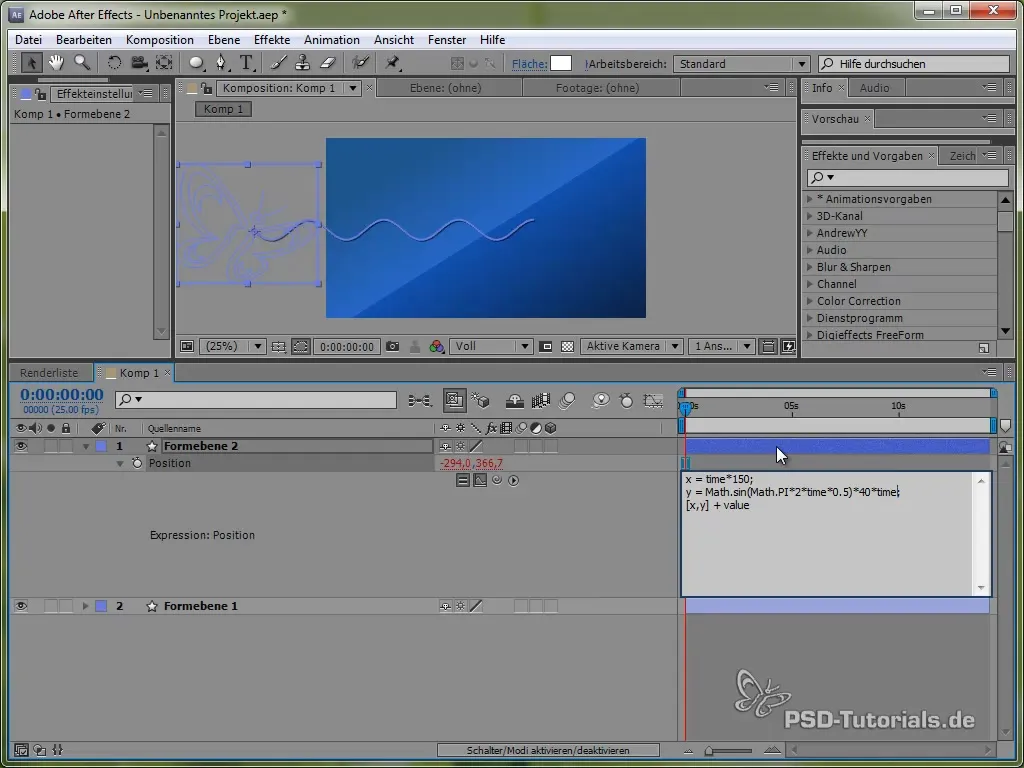
Abychom našeho motýla oživili, musíme ho nejprve animovat tak, aby se pohyboval vlnově. Tato vlnová pohybová animace je snadno realizovatelná pomocí výrazů.

Začni tím, že otevřeš pozici motýla stisknutím klávesy „P“. Poté nastav výraz pro pozici stisknutím klávesy ALT a kliknutím na hodiny.

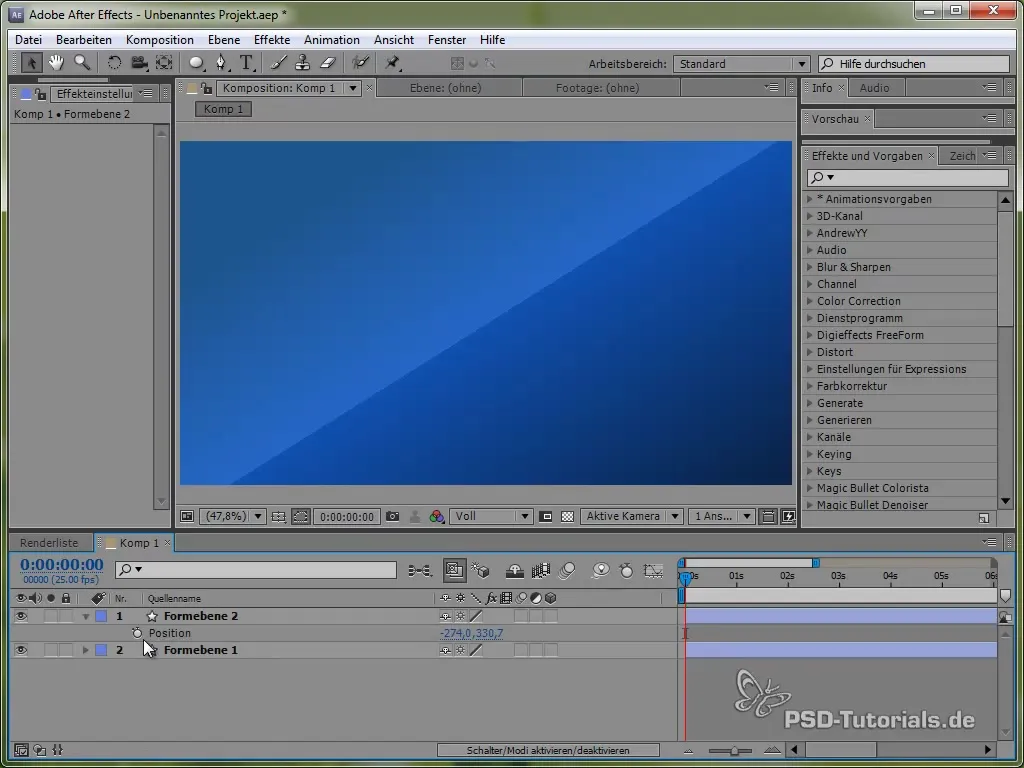
Nejprve k tomu použijeme proměnnou času time, násobenou hodnotou, která určuje rychlost pohybu. Například:

value[0] + time * 150

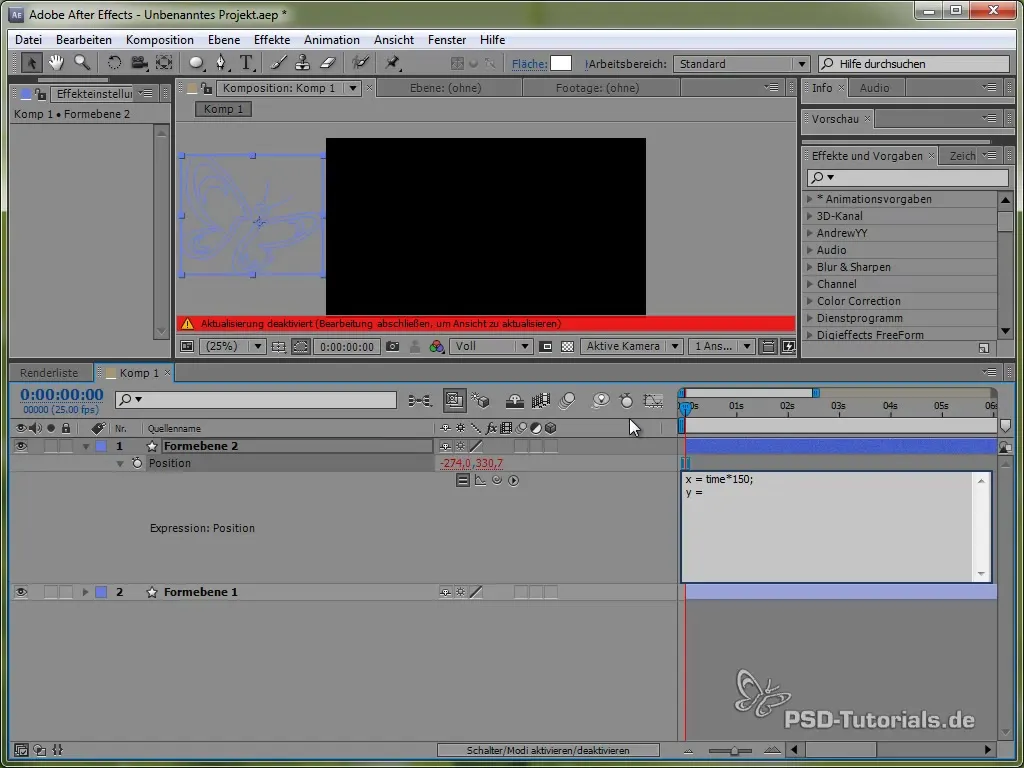
Tento kód způsobí, že se motýl v směru X pohybuje konstantně o 150 pixelů za sekundu. Pro směrem Y použijeme sinusovou funkci, která vytvoří vertikální pohyb motýla a nechá ho „kolísat“ mezi určitými hodnotami.

Aplikace sinusové funkce

Pohyb v ose Y je definován následujícím výrazem:

value[1] + 40 * Math.sin(2 * Math.PI * time)

Přičemž Math.sin() realizuje sinusovou funkci. Ta se pohybuje mezi -1 a 1 a je násobena 40, což znamená, že motýl kolísá v ose Y mezi -40 a 40 pixely.

Vizualizace pohybu

Abychom tuto pohybovou animaci lépe vizualizovali, můžeš aktivovat okno grafu v After Effects. To ti jasně ukáže kolísání hodnot sinusové funkce.

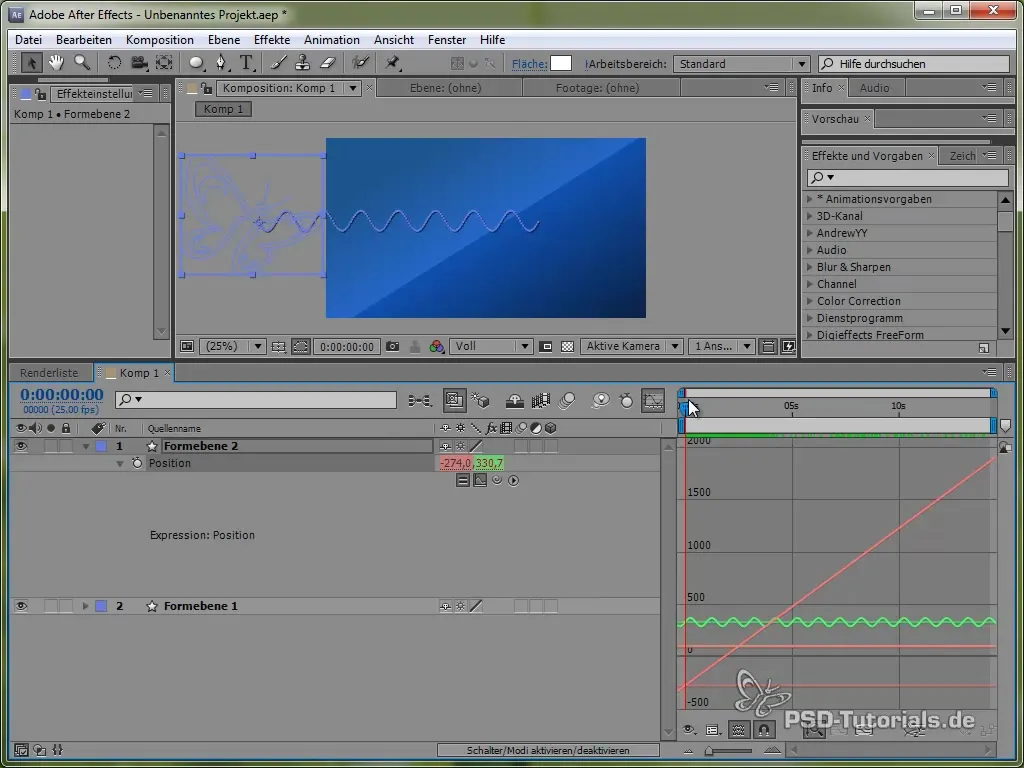
Je vidět, že signál osciluje a pohybuje se přes obrazovku.

Variace amplitudy a frekvence

Teď můžeš upravit amplitudu, aby ses vytvořily různě silné kolísání. Pokud bys chtěl například amplitudu s časem zvýšit, mohl bys použít následující:

40 * (time * 10) * Math.sin(2 * Math.PI * time)

Tím se amplituda časem zvýší, což způsobí, že motýl po jedné sekundě kolísá o 40 pixelů, po dvou sekundách o 80 pixelů a tak dále.

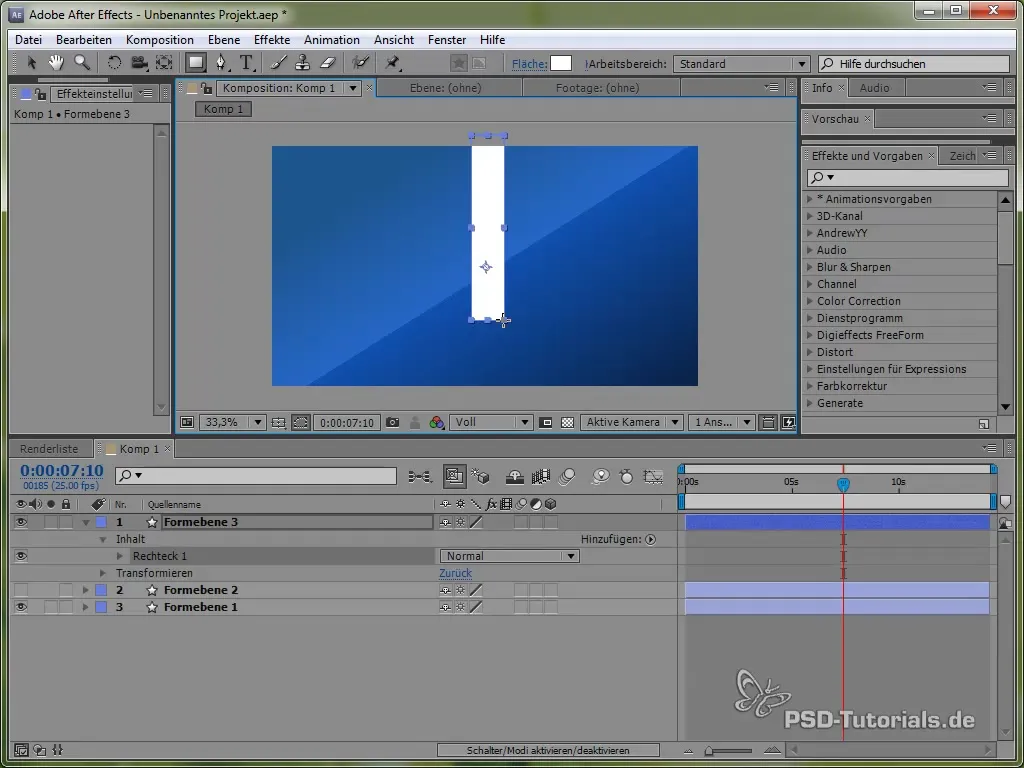
Vytvoření kyvadla

Abychom prohloubili práci s různými fyzikálními simulacemi, nyní se zaměříme na vytvoření kyvadla. Nejprve nakresli tenkou tyč a na jejím konci přidej elipsu.

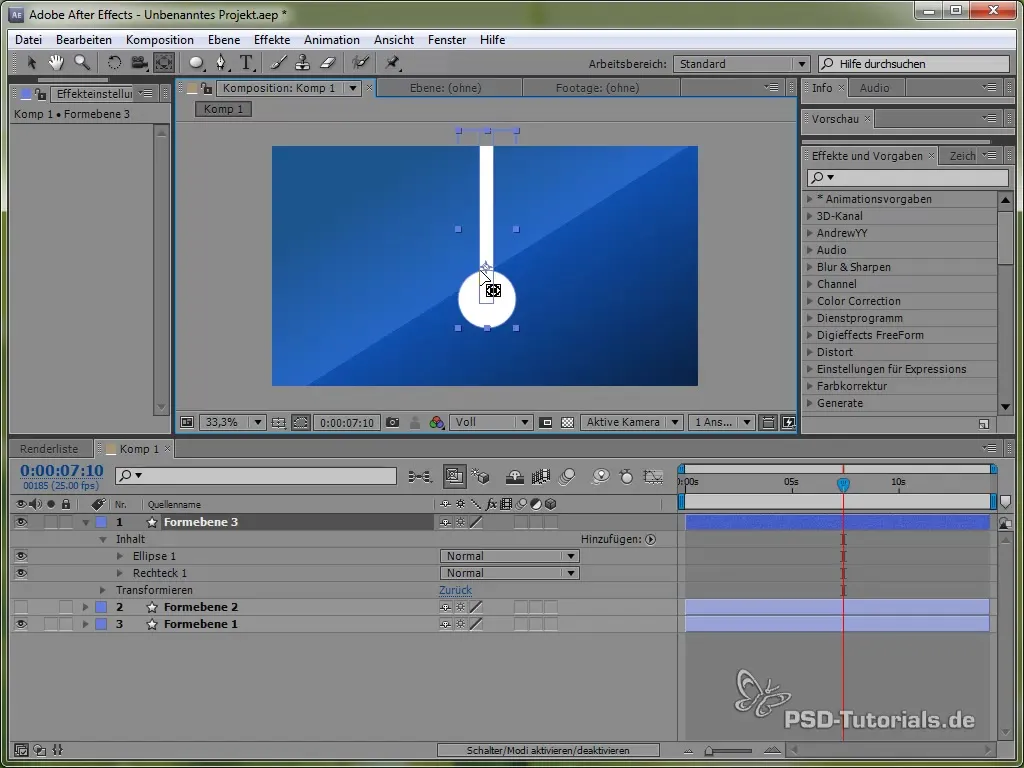
Umísti kotevní bod na vrcholu kyvadla, aby se mohl houpat. To se provádí pomocí nástroje pro kotevní bod.

Poté nastav výraz:

value + 40 * Math.cos(2 * Math.PI * time)

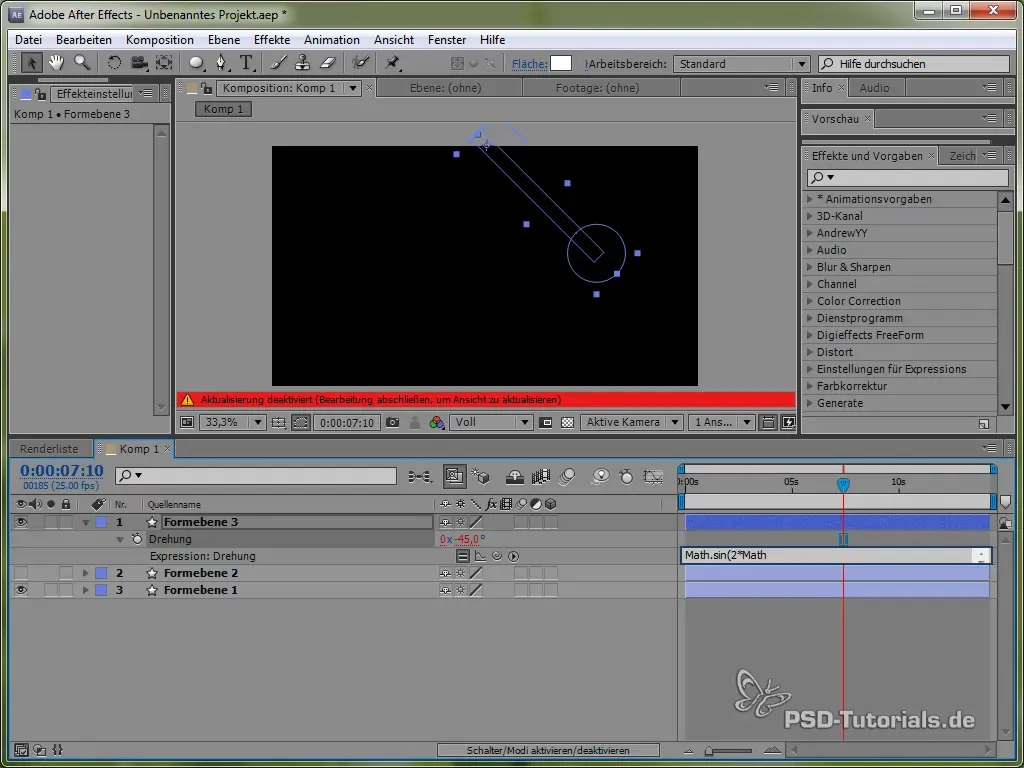
Díky kosinu zahajujeme proces houpání z pozitivního bodu, což je realistické, protože kyvadlo začíná houpáním nahoře.

Přidání tlumících efektů

Abychom do houpání integrovali tlumení, použijeme exponenciální funkci. Tímto způsobem vypadá houpání realističtěji, jelikož na začátku je silné a postupně klesá.

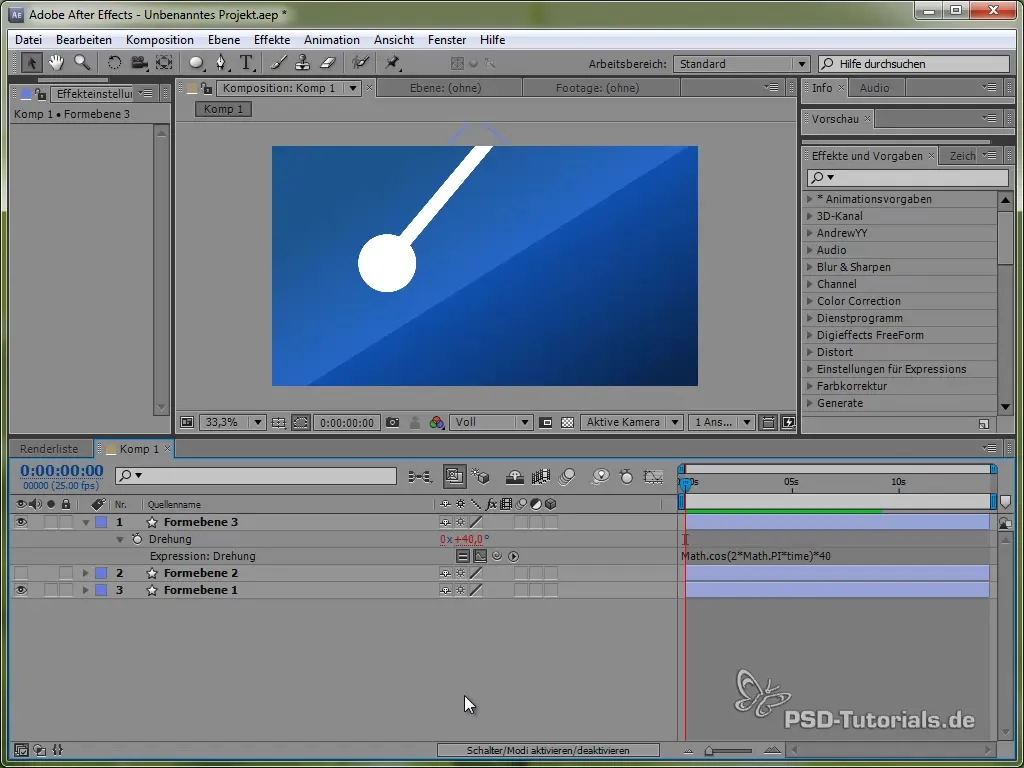
Příklad kódu by mohl vypadat takto:

40 * Math.cos(2 * Math.PI * time) / Math.exp(time)

Zde dělění exponenciální funkcí způsobí pomalé tlumení.

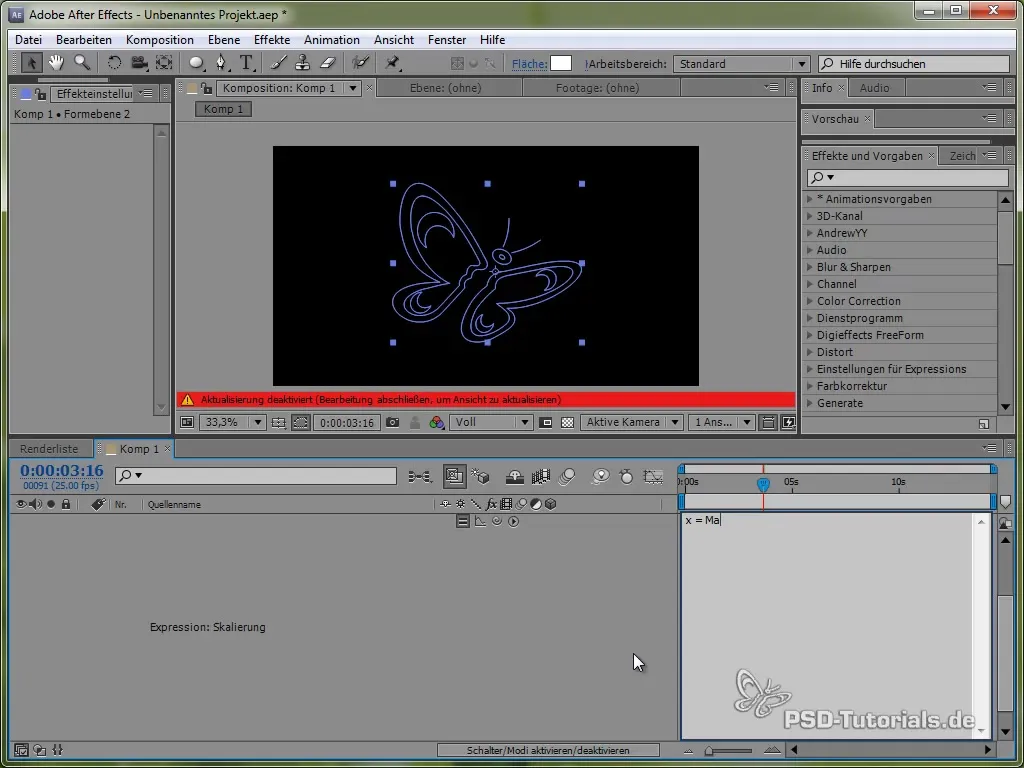
Přidání Squash a Stretch

Pro živější animace můžeš také přidat efekt Squash and Stretch. Toho můžeš dosáhnout pomocí škálování motýla.

Přidáš to tak, že aplikuješ výraz na měřítku, který může být aplikován na hodnoty jak na ose x, tak na ose y, přičemž používáš sinusovou nebo kosinusovou funkci.

Závěrečné myšlenky

Je jasné, že správným použitím trigonometrických a exponenciálních funkcí lze vytvořit velmi realistické a zajímavé animace. Naučil jsi se, jak nechat motýla létat, jak houpat kyvadlo a jak pracovat s efekty jako Squash a Stretch.

Shrnutí - Matematika ve výrazech: Trigonometické & Exponenciální funkce

Matematika v kontextu výrazů v After Effects ti umožňuje vytvářet kreativní a životaschopné animace. Trigonometické a exponenciální funkce jsou při tom nezbytné. V této příručce jsi získal zkušenosti s využitím těchto matematických konceptů v praxi.