Βασικές αρχές των Rechenoperatoren σε Java για αρχάριους

Η κατανόηση των Rechenoperatoren είναι ένα θεμελιώδες μέρος του προγραμματισμού σε Java. Μαθαίνεις όχι μόνο πώς να εκτελείς υπολογισμούς, αλλά και πώς να χειρίζεσαι διάφορους τύπους δεδομένων. Σε αυτόν τον οδηγό, θα επικεντρωθείς στους βασικούς τελεστές που είναι απαραίτητοι για μαθηματικούς υπολογισμούς. Ας ξεκινήσουμε με τις βασικές πτυχές αυτών των τελεστών.

Κύριες επισημάνσεις

Οι Rechenoperatoren στην Java επιτρέπουν βασικές μαθηματικές λειτουργίες. Μαθαίνεις να διακρίνεις μεταξύ αριθμητικών και σύνθετων αλυσίδων και να κατανοείς τις συνέπειες της χρήσης διαφόρων τύπων δεδομένων.

Οδηγίες βήμα προς βήμα

1. Κατανόηση των τελεστών στην Java

Η Java χρησιμοποιεί διάφορους τελεστές για να εκτελεί υπολογισμούς. Οι πιο συχνά χρησιμοποιούμενοι περιλαμβάνουν την πρόσθεση (+), την αφαίρεση (-), τον πολλαπλασιασμό (*) και τη διαίρεση (/). Θα μάθεις πώς λειτουργεί καθένας από αυτούς τους τελεστές και πώς μπορούν να εφαρμοστούν στον κώδικά σου.

2. Δημιούργησε μια κλάση Java για τις αριθμητικές λειτουργίες

Αρχικά, πρέπει να δημιουργήσεις μια νέα κλάση. Ονόμασε αυτή την κλάση για παράδειγμα RechenOperatoren. Σε αυτήν την κλάση θα γράψεις την κύρια μέθοδο main, που ξεκινά το πρόγραμμα σου.

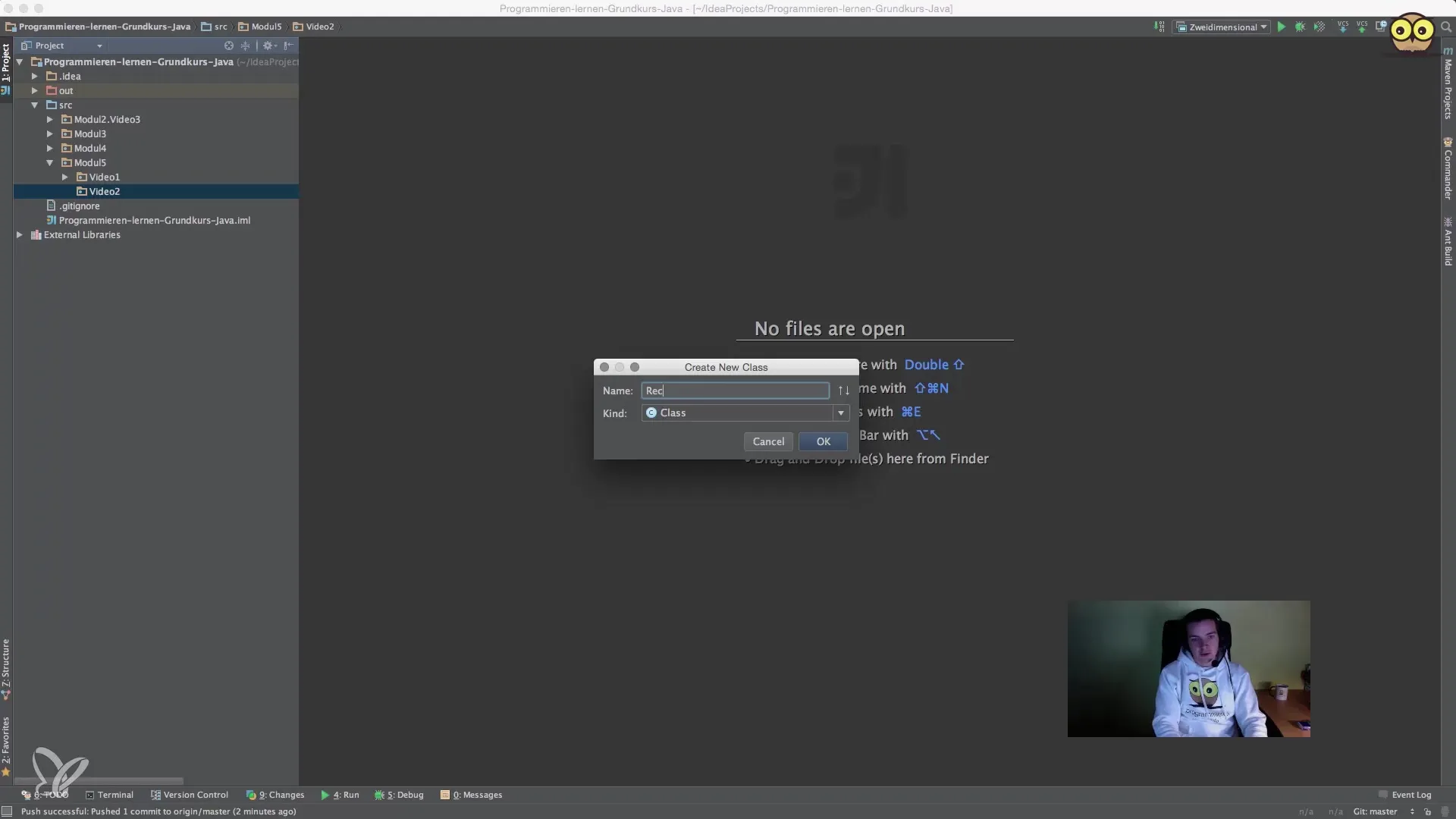
3. Εκτέλεση απλής πρόσθεσης

Με το σύμβολο της πρόσθεσης (+) μπορείς να προσθέσεις δύο αριθμούς. Δημιούργησε μεταβλητές για τους δύο τελεστές, όπως int operand1 = 2; και int operand2 = 3;. Στη συνέχεια μπορείς να υπολογίσεις ένα αποτέλεσμα προσθέτοντας τους δύο τελεστές.

int ergebnis = operand1 + operand2;

Μη ξεχάσεις να εκτυπώσεις το αποτέλεσμα χρησιμοποιώντας τη μέθοδο System.out.print().

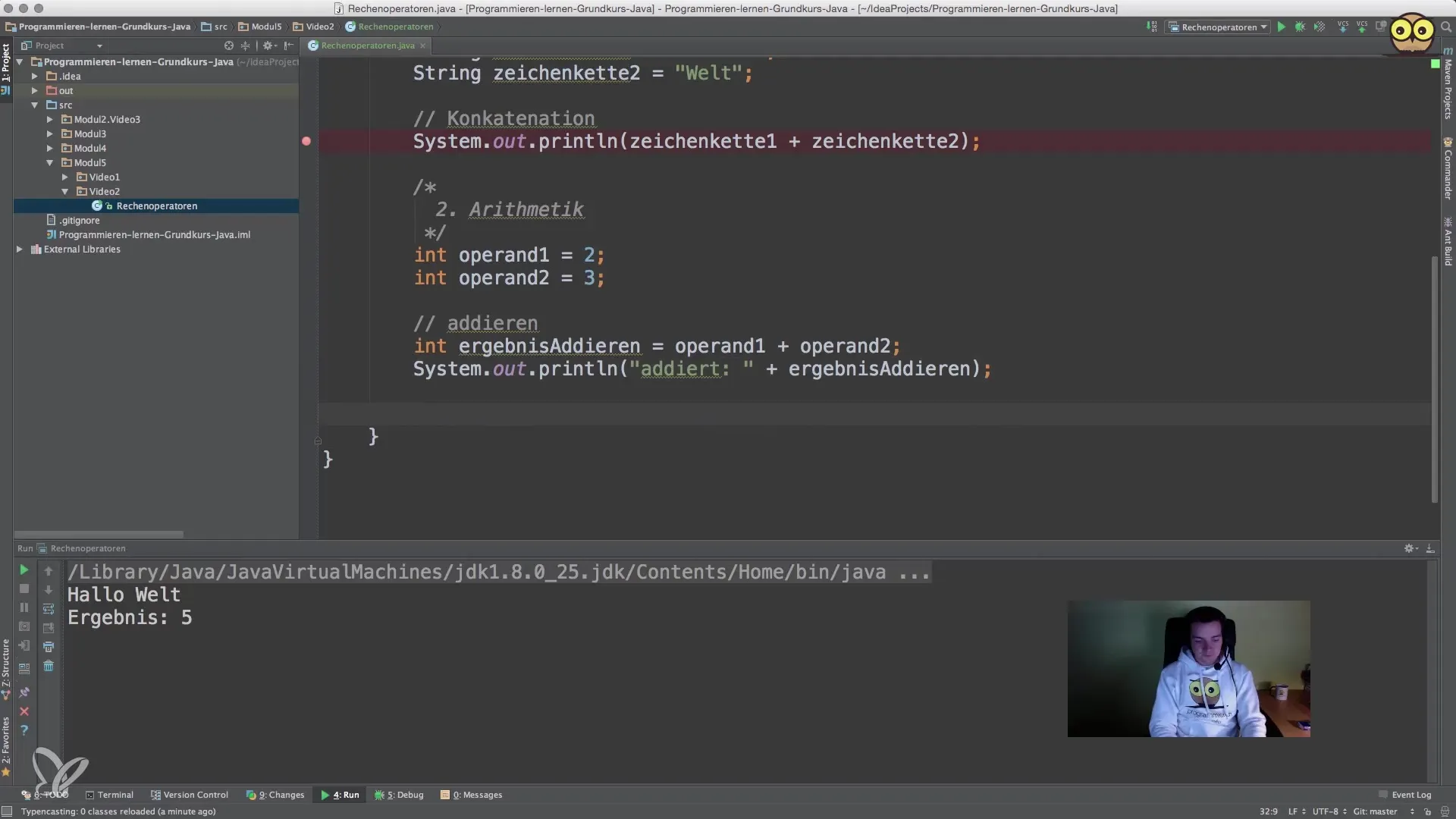
4. Εφαρμογή αφαίρεσης

Ο τελεστής αφαίρεσης (-) λειτουργεί παρόμοια με το σύμβολο της πρόσθεσης. Ορίστε ξανά δύο τελεστές και εκτέλεσε στη συνέχεια την αφαίρεση. Για παράδειγμα, μπορείς να υπολογίσεις όπως ακολουθεί:

int subtraktionErgebnis = operand2 - operand1;

Και αυτό το αποτέλεσμα θα πρέπει επίσης να το εκτυπώσεις.

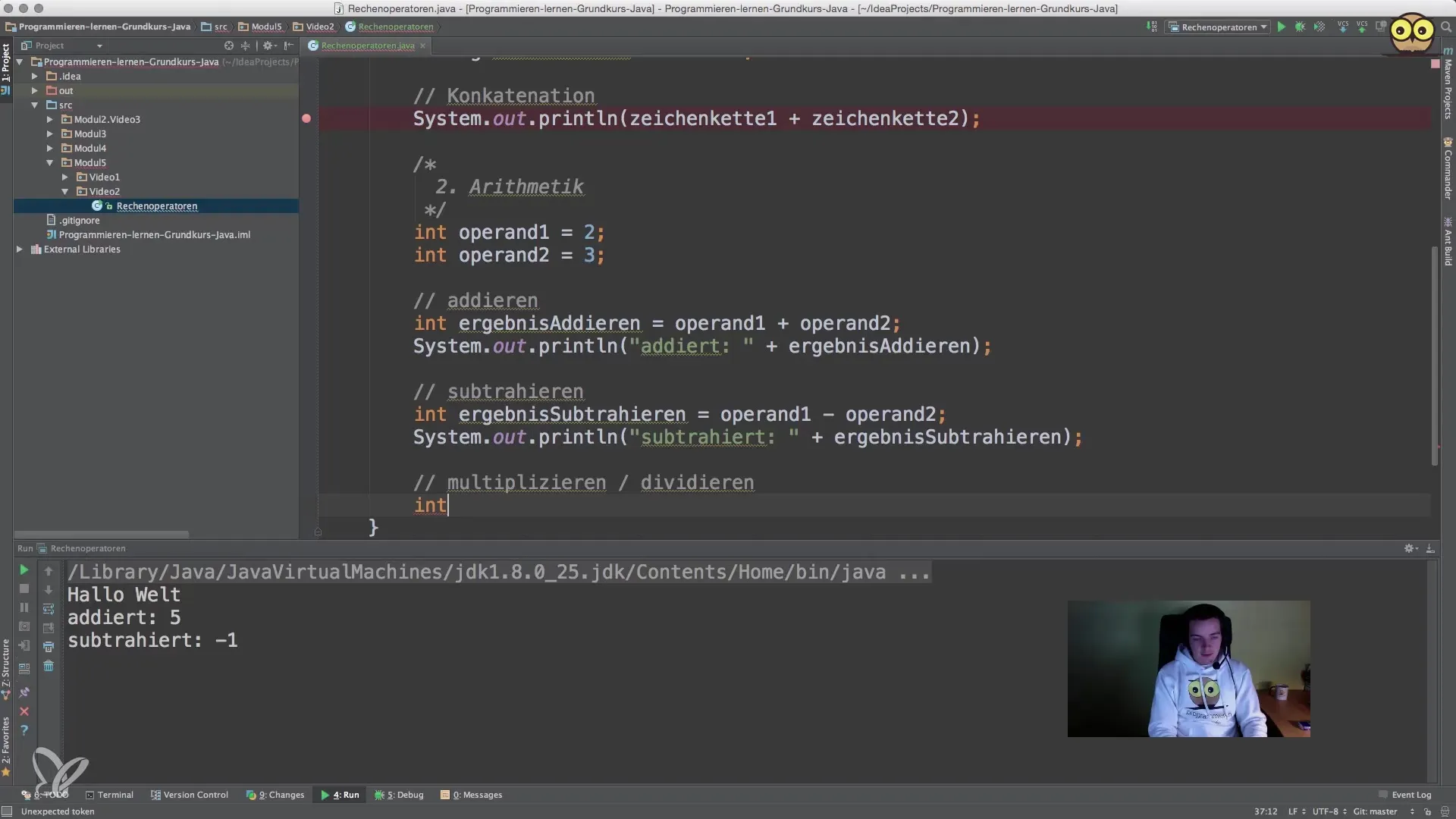
5. Πολλαπλασιασμός

Ο πολλαπλασιασμός γίνεται στην Java με το αστερίσκο (*). Μπορείς να χρησιμοποιήσεις τους προηγουμένως καθορισμένους τελεστές για να υπολογίσεις το προϊόν.

int multiplizierenErgebnis = operand1 * operand2;

Βεβαιώσου ότι θα εκτυπώσεις το αποτέλεσμα με τη μέθοδο Print.

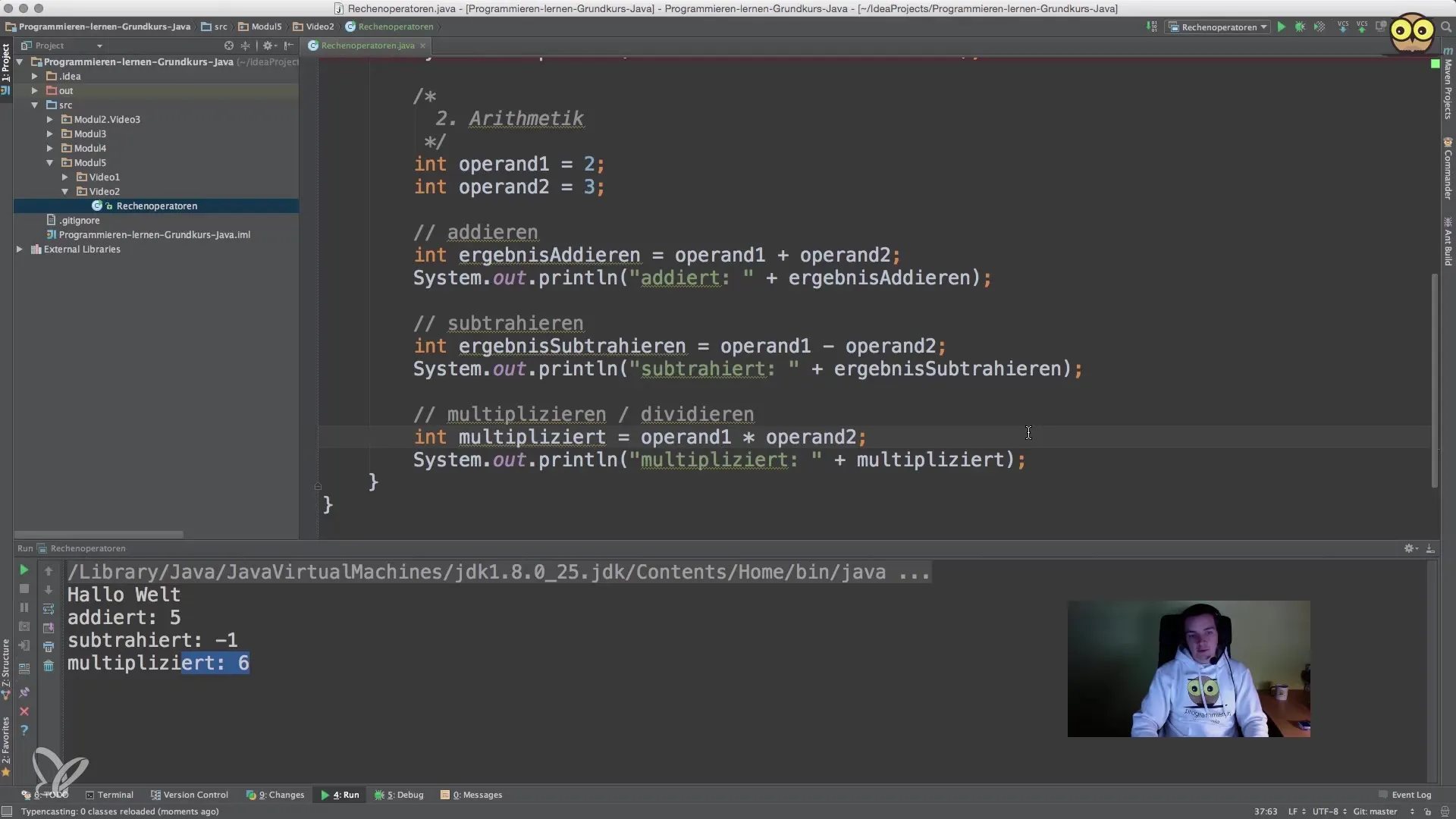
6. Εκτέλεση διαίρεσης

Δίπλωσε τις τιμές με την κάθετη (/). Εδώ είναι σημαντικό να προσέξεις με ποιους τύπους δεδομένων εργάζεσαι. Η διαίρεση ακέραιων αριθμών συχνά δίνει ακέραιο αποτέλεσμα και τα δεκαδικά μπορεί να απορριφθούν. Προσαρμόσου χρησιμοποιώντας μια τιμή double για να πετύχεις πιο ακριβή αποτελέσματα.

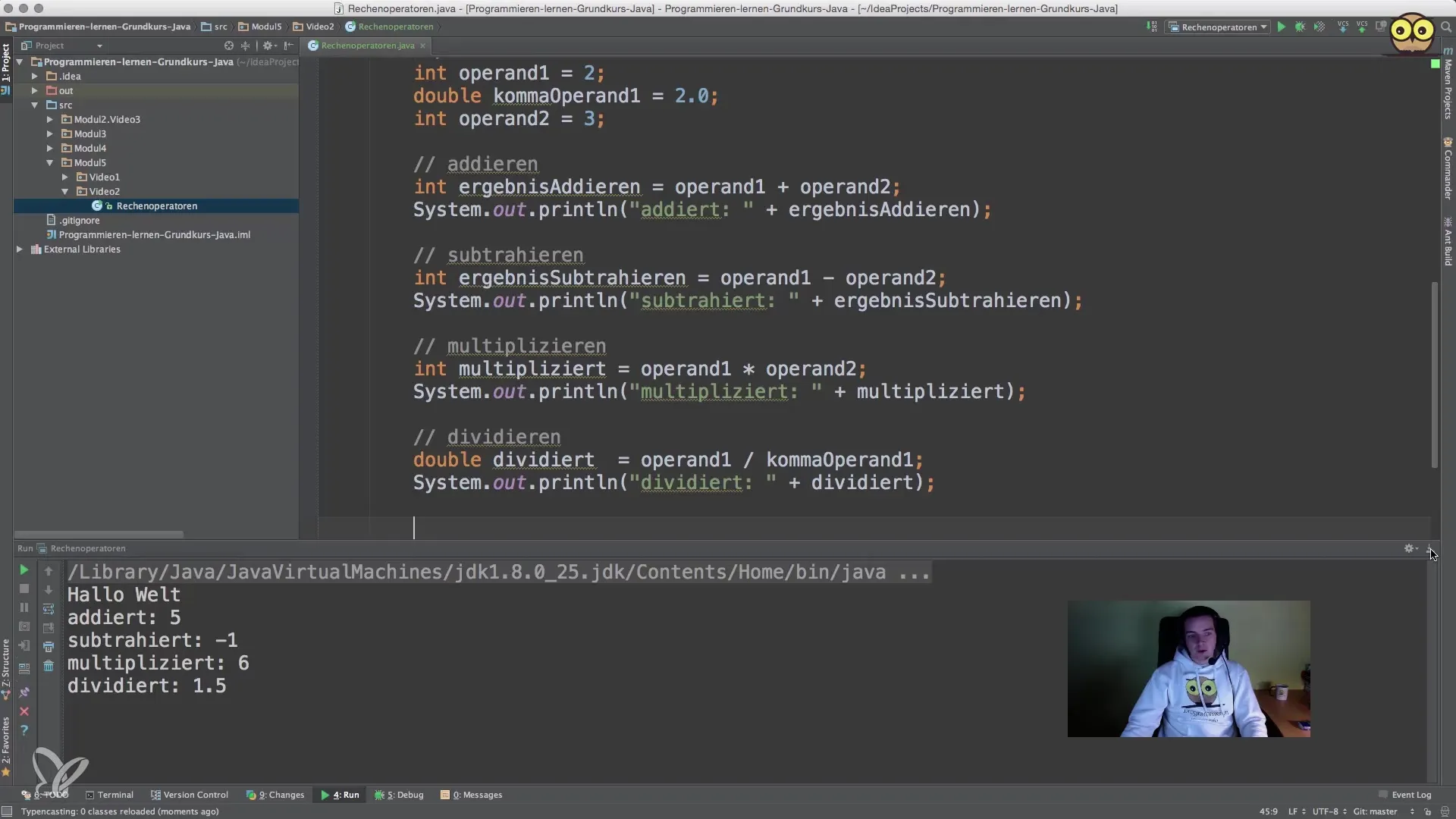
7. Χρήση της λειτουργίας Modulo

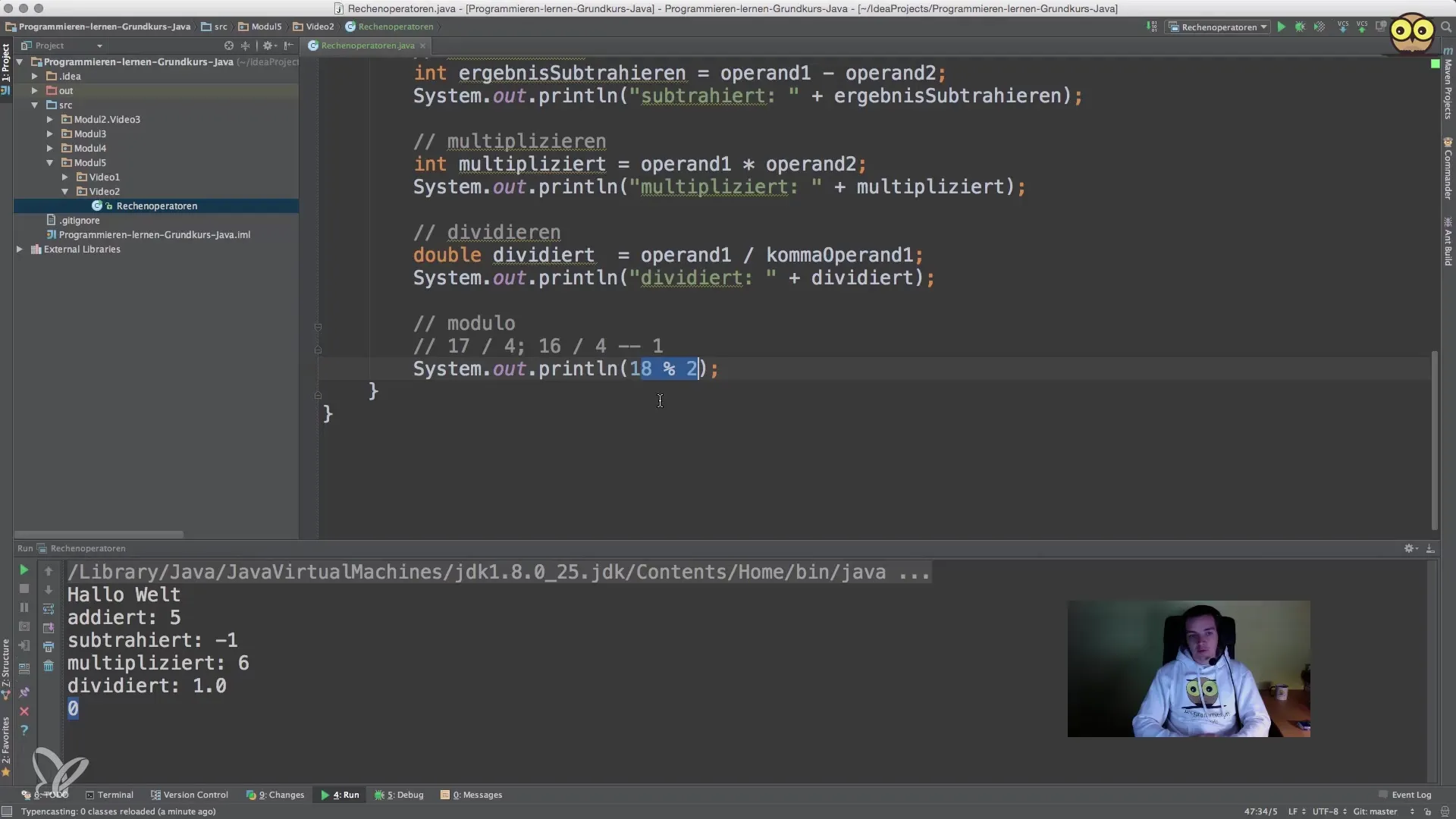
Με τον τελεστή Modulo (%) μπορείς να υπολογίσεις το υπόλοιπο μιας διαίρεσης. Για παράδειγμα, μπορείς να χρησιμοποιήσεις 17 % 4 για να δεις ποιο είναι το υπόλοιπο. Αυτή η τεχνική είναι χρήσιμη για να διαπιστώσεις αν ένας αριθμός είναι άρτιος ή περιττός.

8. Περίληψη των αριθμητικών λειτουργιών

Για να οπτικοποιήσεις τις αριθμητικές λειτουργίες σου, μπορείς να εφαρμόσεις μια επιλογή προεπισκόπησης στον κώδικά σου, η οποία θα εμφανίζει τα αποτελέσματα των διαφόρων υπολογισμών. Αυτό σε βοηθά να διατηρείς μια σαφή εικόνα των αποτελεσμάτων.

Περίληψη – Rechenoperatoren στην Java: Βασικές γνώσεις για αρχάριους

Σε αυτόν τον οδηγό, έχεις μάθει τις κύριες αριθμητικές λειτουργίες στην Java. Η κατανόηση των διαφόρων τελεστών και η σωστή εφαρμογή τους είναι καθοριστική για την ανάπτυξη αποτελεσματικών προγραμμάτων και την αποφυγή τυπικών λαθών.