Matematiikka lausekkeissa: Trigonometristen ja eksponentiaalisten konseptien mukaisesti

Matematiikka näyttelee digitaalimaailmassa keskeistä roolia, ja erityisesti videonmuokkauksessa After Effects (AE) -ohjelmalla se avaa täysin uusia mahdollisuuksia. Tässä oppaassa opit, kuinka voit käyttää trigonometristä ja ekspotentiaalista funktiota AE:ssä Expressions -toimintona luodaksesi kiehtovia animaatioita. Erityisen mielenkiintoinen esimerkki on perhosen liike, joka näyttää, miten fysiikan simulaatioita voidaan toteuttaa matematiikan avulla.

Tärkeimmät havainnot

• Trigonometrisiä funktioita, kuten sin ja cos, voidaan käyttää siirtyvien liikkeiden luomiseen.
• Ekspotentiaalisia funktioita käytetään vaimennusvaikutusten simuloimiseen.
• Absoluuttisten arvojen käyttäminen funktioissa voi auttaa saavuttamaan tiettyjä animaatioefektejä.

Perhonen liikkuu

Jotta perhosemme liikkuisi, sinun on ensin animoitava se niin, että se liikkuu aallossa. Tämä aaltoilu on helppo toteuttaa Expressionsin avulla.

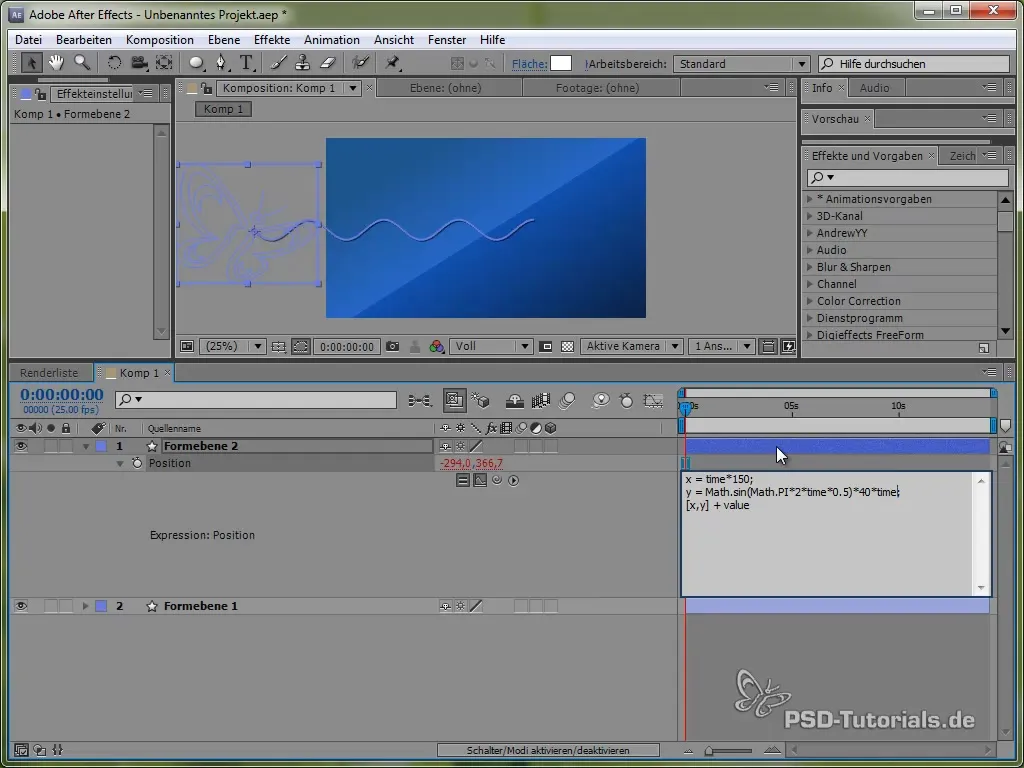
Aloita avaamalla perhosen sijainti painamalla "P"-näppäintä. Aseta sitten Expression sijainnille painamalla ALT-näppäintä ja klikkaamalla kelloa.

Tähän käytämme ensin aikamuuttuja time, joka kerrotaan arvolla, joka määrittää liikkeen nopeuden. Esimerkiksi:

value[0] + time * 150

Tämä koodi saa perhosen liikkumaan X-suunnassa jatkuvasti 150 pikseliä sekunnissa. Y-suunnassa käytämme sinifunktiota, joka luo perhosen pystysuuntaista liikettä ja saa sen "heilahtelemaan" tiettyjen arvojen välillä.

Sinifunktion soveltaminen

Y-liike määritellään seuraavalla Expressionilla:

value[1] + 40 * Math.sin(2 * Math.PI * time)

Tässä Math.sin() toteuttaa sinifunktion. Se vaihtelee -1:n ja 1:n välillä ja kerrotaan 40:llä, mikä tarkoittaa, että perhonen heilahtelee Y-suunnassa -40 ja 40 pikselin välillä.

Liikegrafiikan visualisointi

Jotta tämä liike olisi helpompi visualisoida, voit aktivoida grafiikkaruudun After Effectsissä. Tämä näyttää sinimuotoisen arvon vaihtelut selkeämmin.

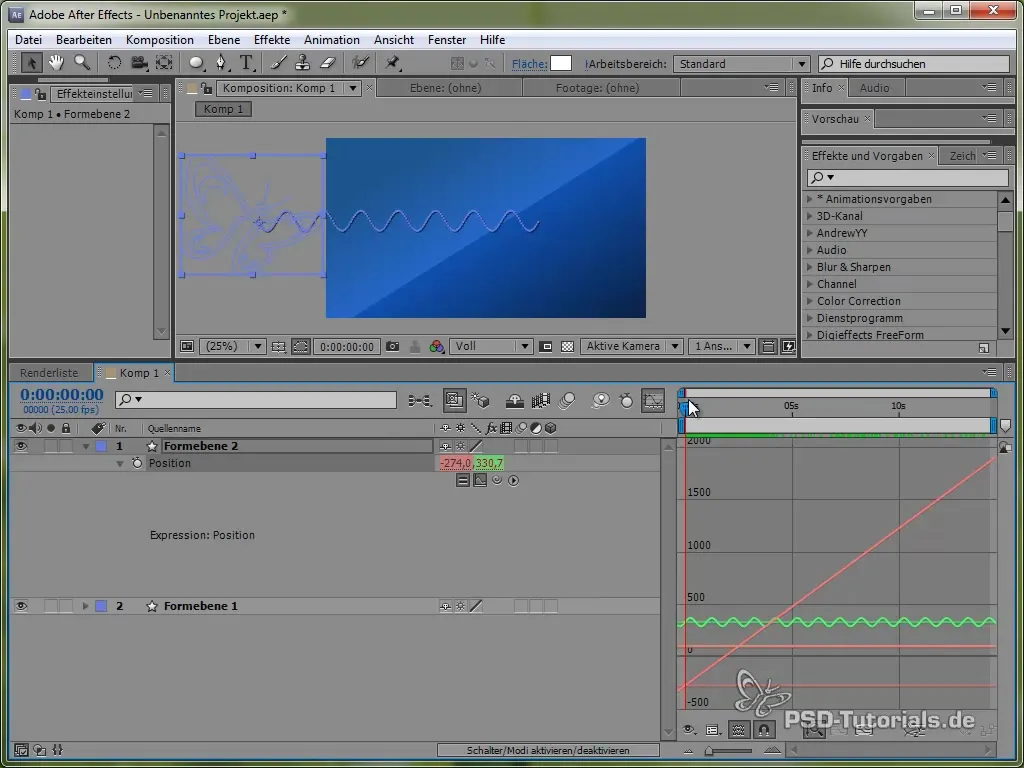
Näet, että signaali振荡itas ja liikkuu yli näytön.

Amplitudi ja taajuus

Nyt voit säätää amplitudia, jotta saat erilaisia heilahteluita. Esimerkiksi, jos haluat kasvattaa amplitudia ajan myötä, voit käyttää seuraavaa:

40 * (time * 10) * Math.sin(2 * Math.PI * time)

Tällä tavoin amplitudi kasvaa ajan myötä, mikä tarkoittaa, että perhonen heilahtelee yhden sekunnin jälkeen 40 pikseliä, kahden sekunnin jälkeen 80 pikseliä ja niin edelleen.

Keinotekoisen luominen

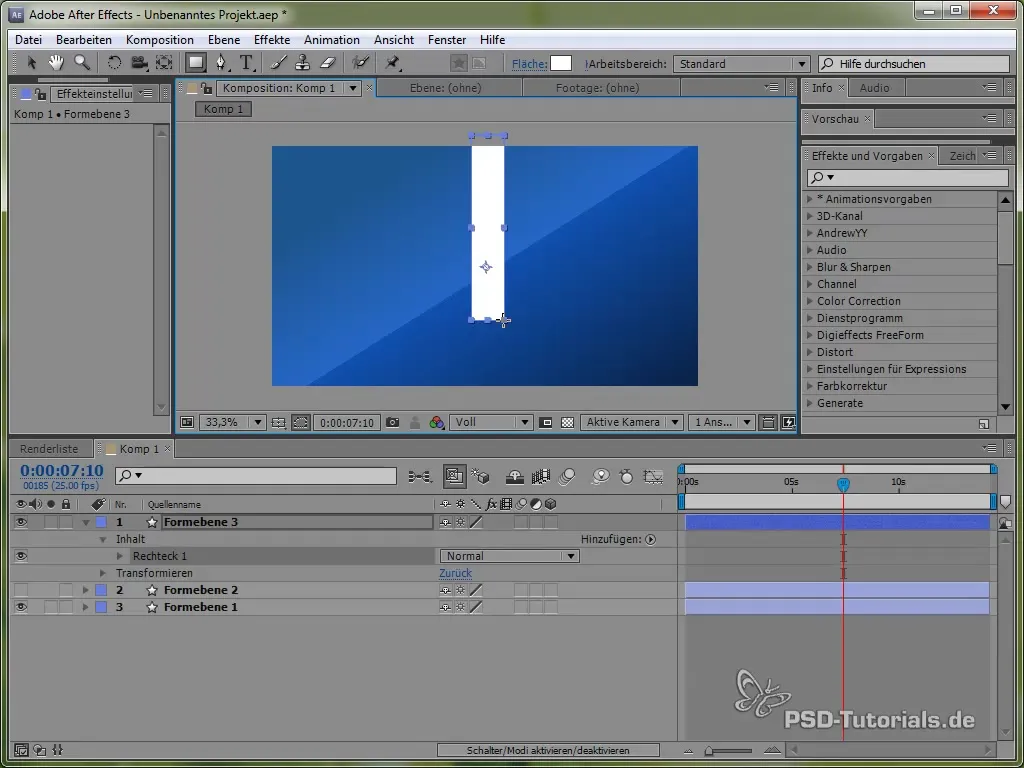
Syventääksemme käsittelyä erilaisista fysiikan simulaatioista, käännymme nyt keinon valmistamiseen. Piirrä ensin ohut sauva ja lisää ellipsi sen päähän.

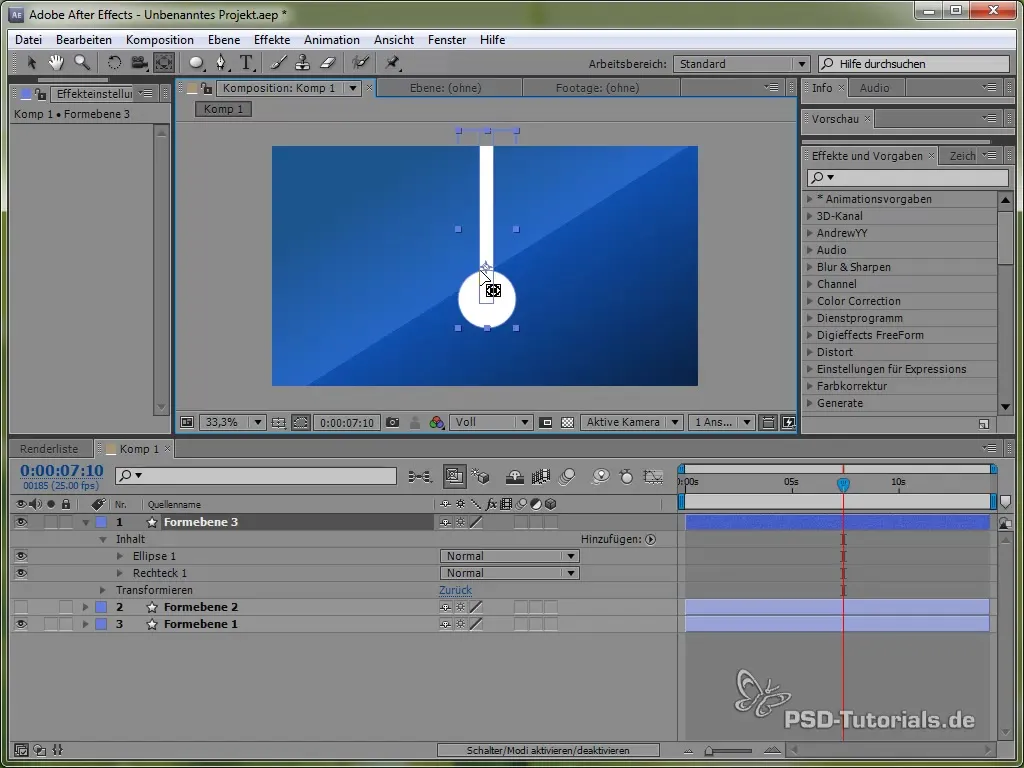
Aseta kiinnityspiste keinon ylle niin, että se voi heilua. Tämä tapahtuu kiinnityskohtatyökalun avulla.

Aseta sitten Expression:

value + 40 * Math.cos(2 * Math.PI * time)

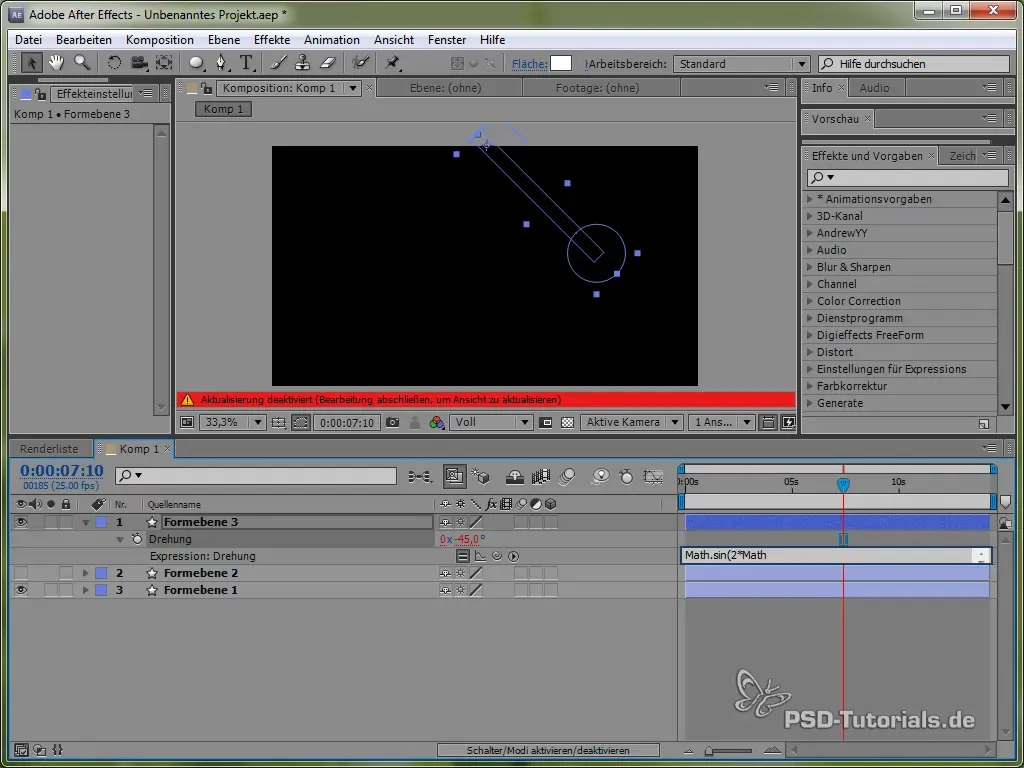
Cosinuksen avulla aloitamme heilumisprosessin positiivisesta pisteestä, mikä on realistista, koska keinon liike alkaa ylhäältä.

Vaimennusvaikutusten lisääminen

Integroimalla vaimennusliikeemme, käytämme eksponentiaalista funktiota. Tämä tekee liikku misesta realistisempaa, koska se on aluksi voimakas ja laskee lopuksi.

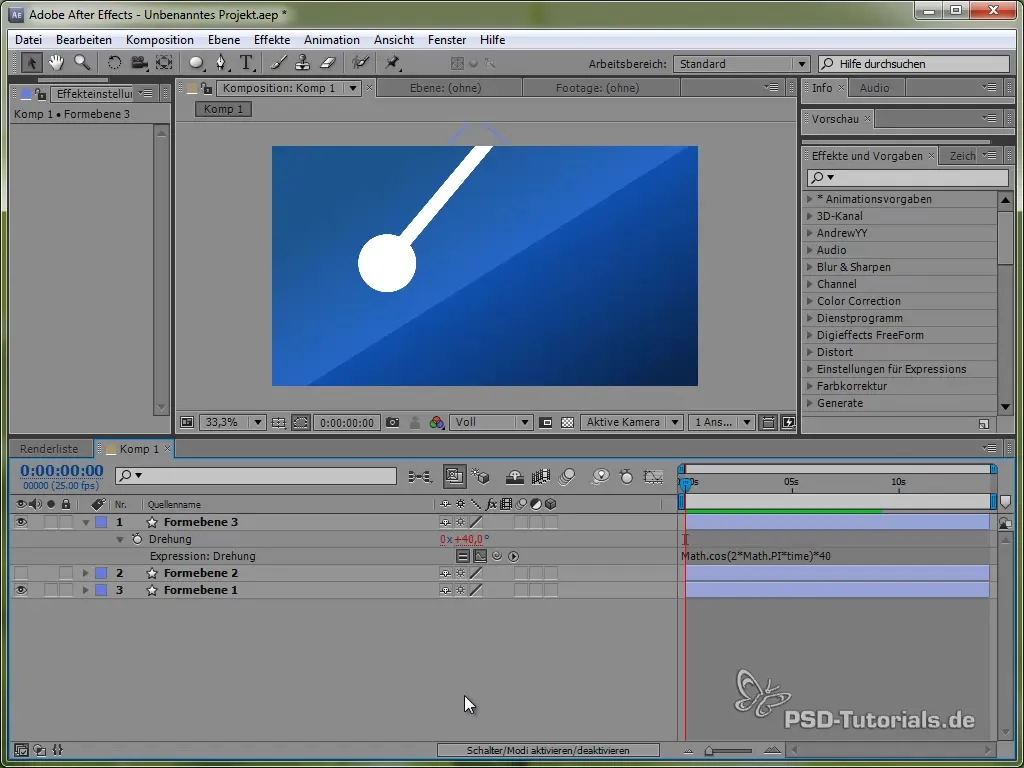
Esimerkkikoodi voisi näyttää tältä:

40 * Math.cos(2 * Math.PI * time) / Math.exp(time)

Tässä jakaminen eksponentiaalifunktiolla tuottaa hitaita vaimennuksia.

Squash ja Stretch

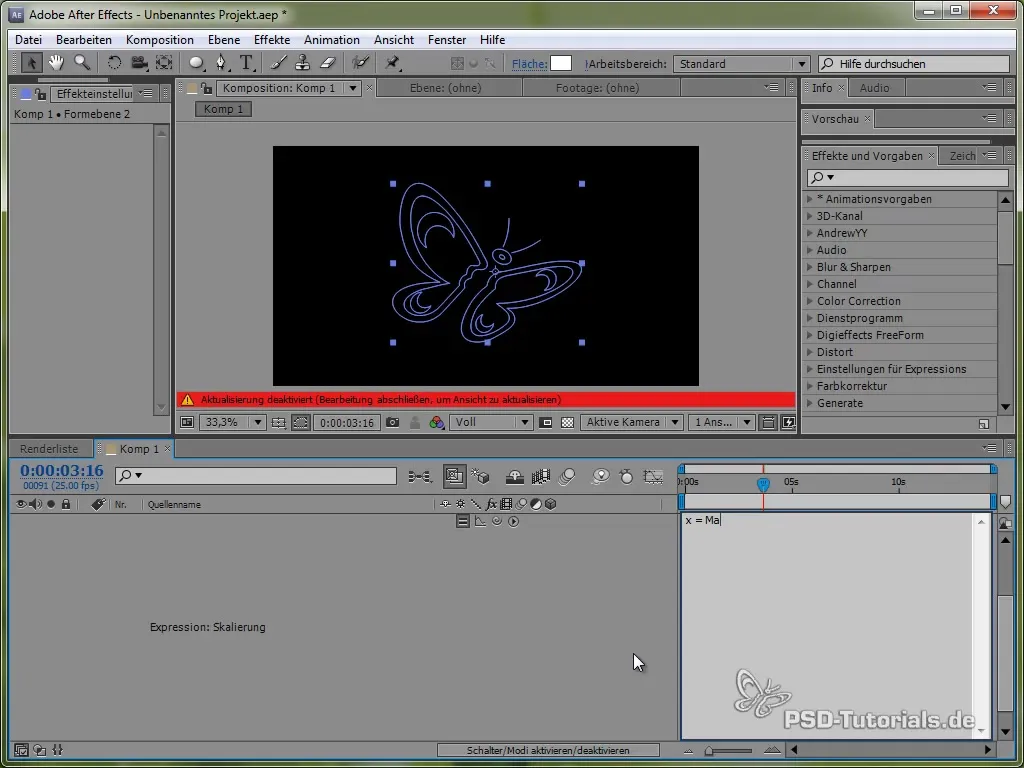
Elävimpiä animaatioita varten voit myös lisätä Squash and Stretch -efektin. Voit saavuttaa tämän perhosen skaalausta muokkaamalla.

Teet tämän soveltamalla Expressionia skaalausasteikkoon, joka voidaan soveltaa sekä x- että y-arvoihin käyttäen joko sin- tai cos-funktiota.

Lopulliset ajatukset

Näet, että oikealla trigonometristen ja eksponentiaalisten funktioiden soveltamisella voidaan luoda erittäin realistisia ja mielenkiintoisia animaatioita. Olet oppinut, kuinka saada perhonen lentämään, keinottamaan ja kuinka työskennellä Squash and Stretch -efektien kanssa.

Yhteenveto - Matematiikka Expressioneissa: Trigonometriset & Eksponentiaaliset Funktiot

Matematiikka Expressions-yhteydessä After Effectsissä avaa sinulle mahdollisuuden luoda luovia ja eloisia animaatioita. Trigonometristen ja eksponentiaalisten funktioiden osalta on olennaista. Tässä oppaassa olet saanut kokemuksia näiden matemaattisten Käsitteiden käytöstä käytännössä.