Les mathématiques jouent un rôle fondamental dans le monde numérique et en particulier dans le montage vidéo avec After Effects (AE), elles t'offrent de tout nouvelles possibilités. Dans ce tutoriel, tu vas apprendre comment utiliser les fonctions trigonométriques et exponentielles dans AE en tant que Expressions, pour créer des animations fascinantes. Un exemple particulièrement passionnant sera le mouvement d'un papillon, qui te montrera comment des simulations physiques peuvent être mises en œuvre grâce aux mathématiques.
Principales conclusions
- Les fonctions trigonométriques comme le sinus et le cosinus peuvent être utilisées pour créer des mouvements décalés.
- Les fonctions exponentielles sont utilisées pour simuler des effets d'atténuation.
- L'utilisation de valeurs absolues dans les fonctions peut aider à obtenir certains effets d'animation.
Guide étape par étape
Mettre en mouvement le papillon
Pour mettre notre papillon en mouvement, tu dois d'abord l'animer de telle manière qu'il se déplace en vagues. Ce mouvement de vagues peut être réalisé sans trop d'effort grâce aux Expressions.
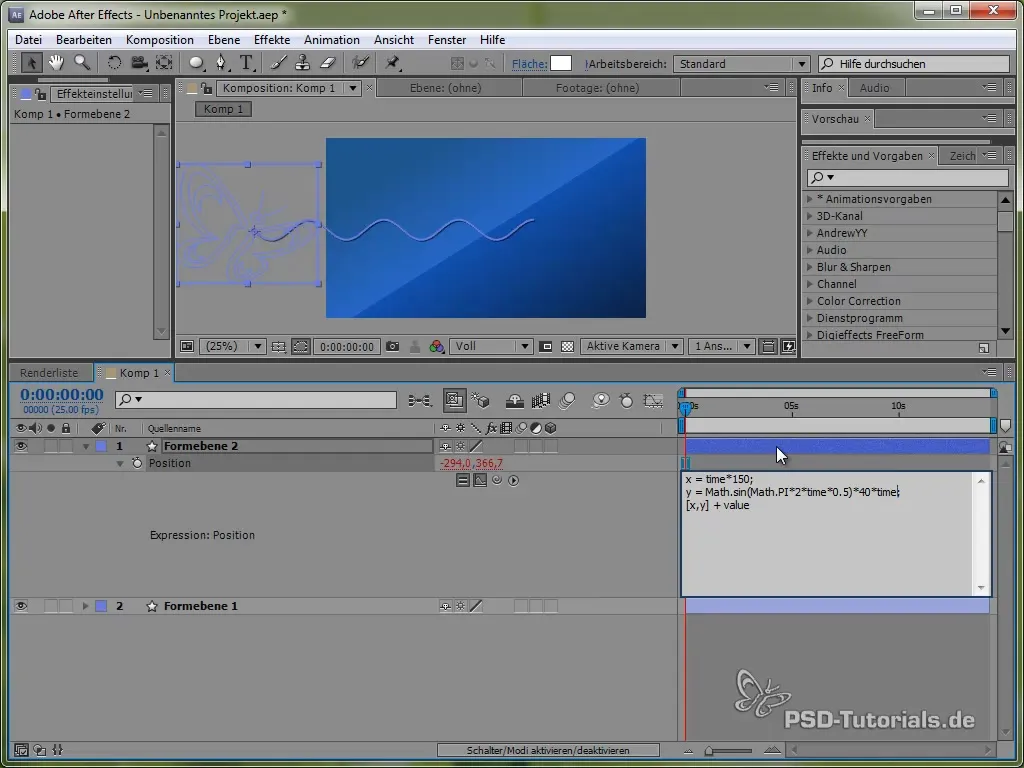
Commence par ouvrir la position du papillon en appuyant sur la touche «P». Ensuite, définis une Expression pour la position en maintenant la touche ALT enfoncée et en cliquant sur l'horloge.
Pour cela, nous utilisons d'abord la variable temps time, multipliée par une valeur qui détermine la vitesse du mouvement. Par exemple :
value[0] + time * 150
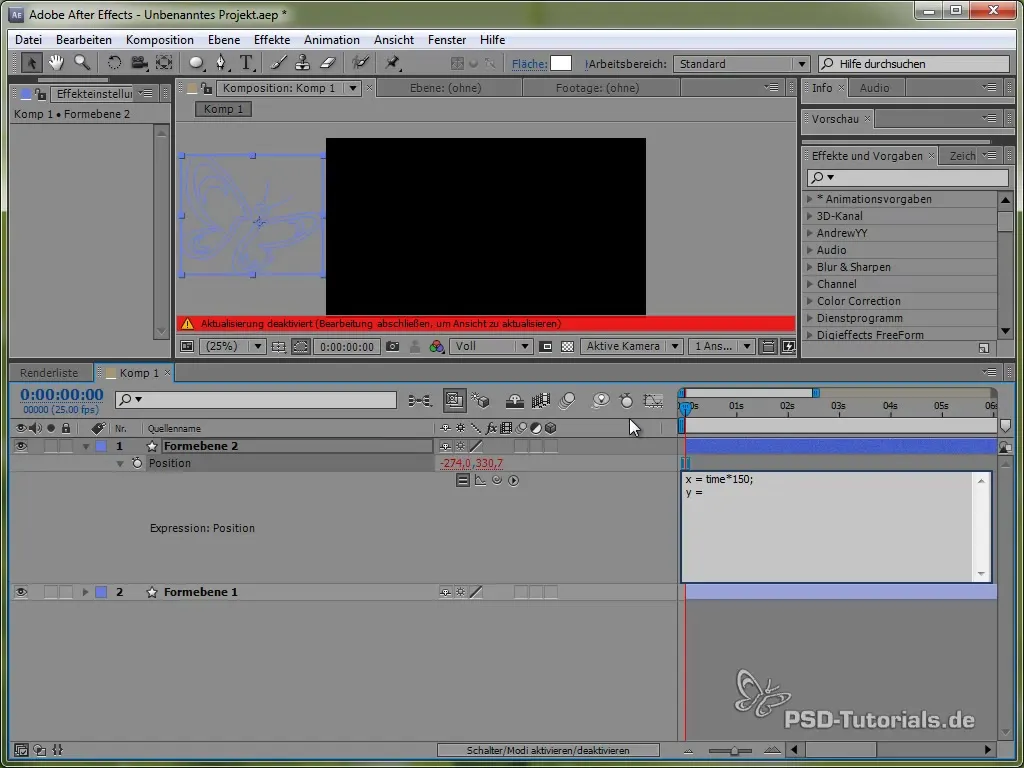
Ce code fait en sorte que le papillon se déplace de manière constante de 150 pixels par seconde sur l'axe X. Pour l'axe Y, nous allons utiliser une fonction sinus qui produira le mouvement vertical du papillon et lui permettra de «flotter» entre certaines valeurs.
Application de la fonction sinus
Le mouvement vertical est défini par l'expression suivante :
value[1] + 40 * Math.sin(2 * Math.PI * time)
Ici, Math.sin() applique la fonction sinus. Elle varie entre -1 et 1 et est multipliée par 40, ce qui signifie que le papillon fluctue entre -40 et 40 pixels sur l'axe Y.
Visualiser la graphique de mouvement
Pour mieux visualiser ce mouvement, tu peux activer la fenêtre de graphique dans After Effects. Cela te montrera plus clairement les fluctuations de la valeur sinus.
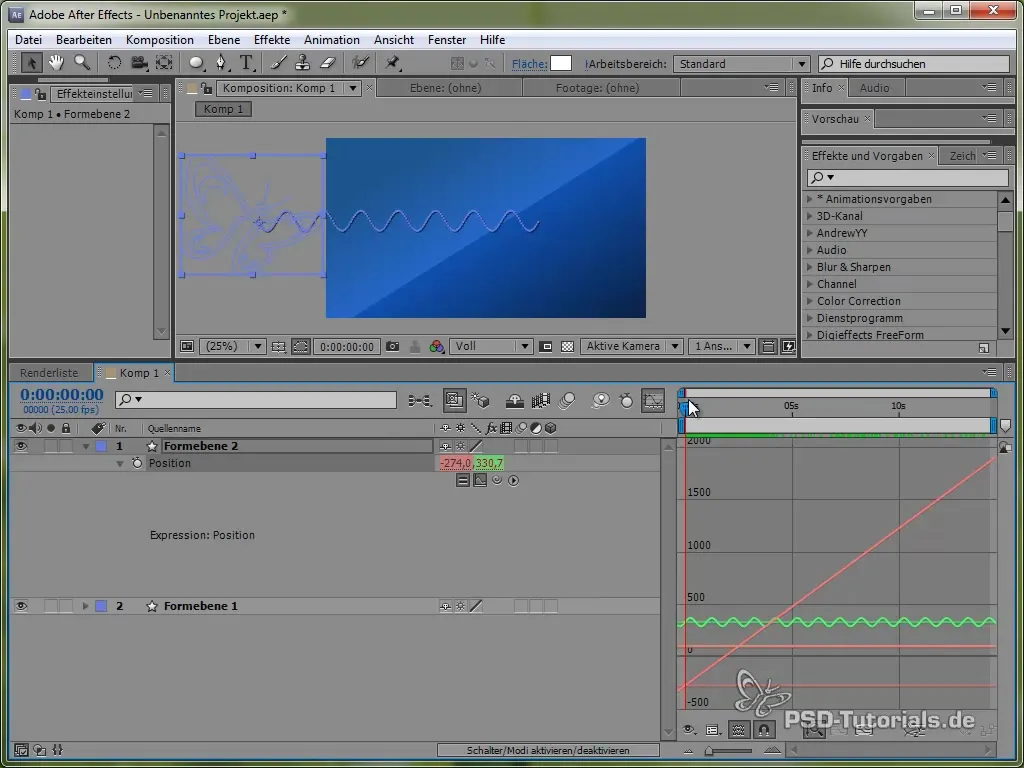
On voit que le signal oscille et se déplace à travers l'écran.
Varier l'amplitude et la fréquence
Maintenant, tu peux ajuster l'amplitude pour créer des oscillations de différentes intensités. Par exemple, si tu souhaites augmenter l'amplitude au fil du temps, tu pourrais utiliser :
40 * (time * 10) * Math.sin(2 * Math.PI * time)
Avec cela, l'amplitude va augmenter avec le temps, ce qui signifie que le papillon va oscillera de 40 pixels après une seconde, de 80 pixels après deux secondes, et ainsi de suite.
Créer un pendule
Pour approfondir la manipulation de diverses simulations physiques, nous allons maintenant nous concentrer sur la création d'un pendule. Dessine d'abord une fine tige et ajoute une ellipse à son extrémité.
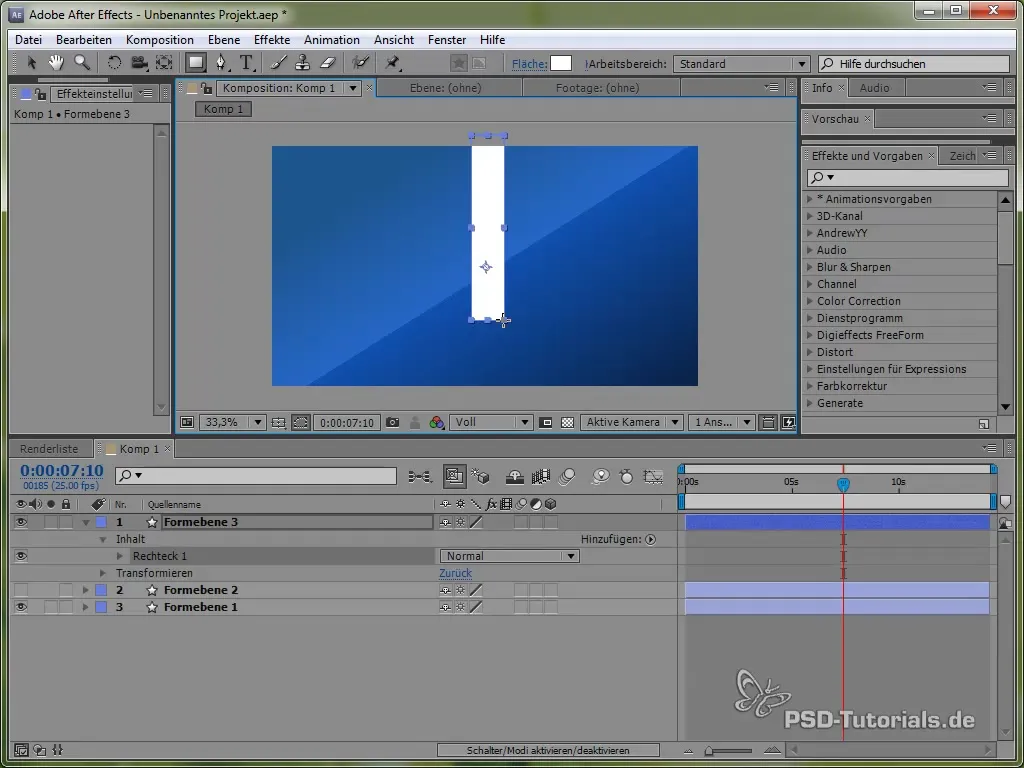
Positionne le point d'ancrage en haut du pendule, afin qu'il puisse osciller. Cela se fait avec l'outil de point d'ancrage.
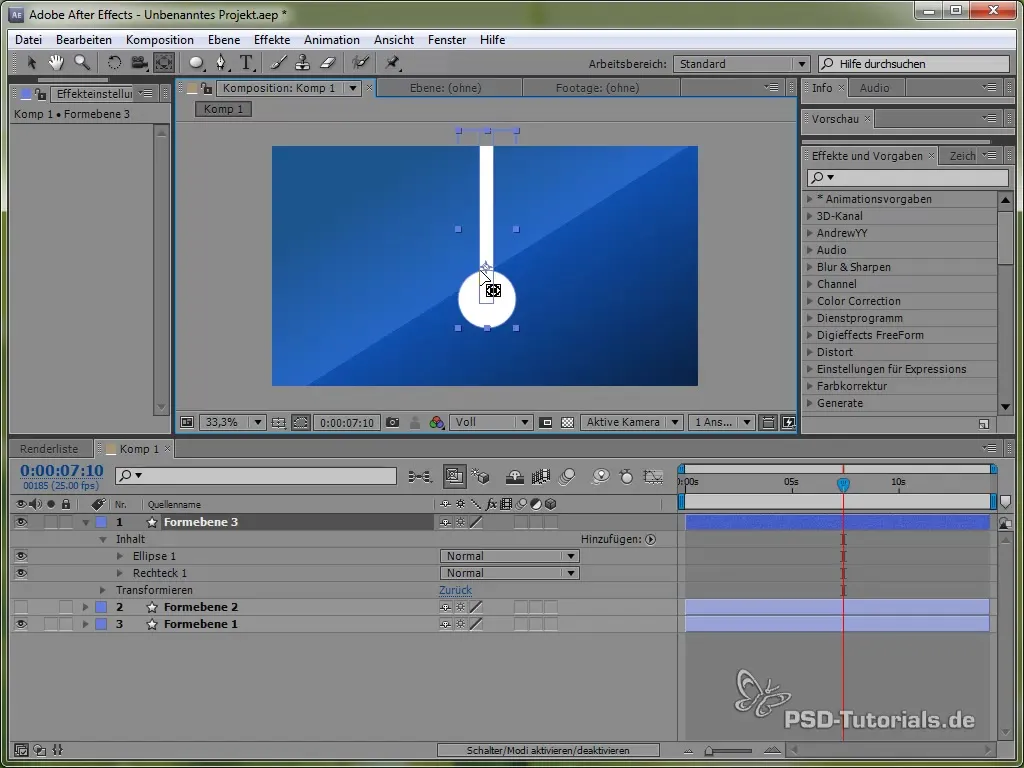
Ensuite, sets l'Expression :
value + 40 * Math.cos(2 * Math.PI * time)
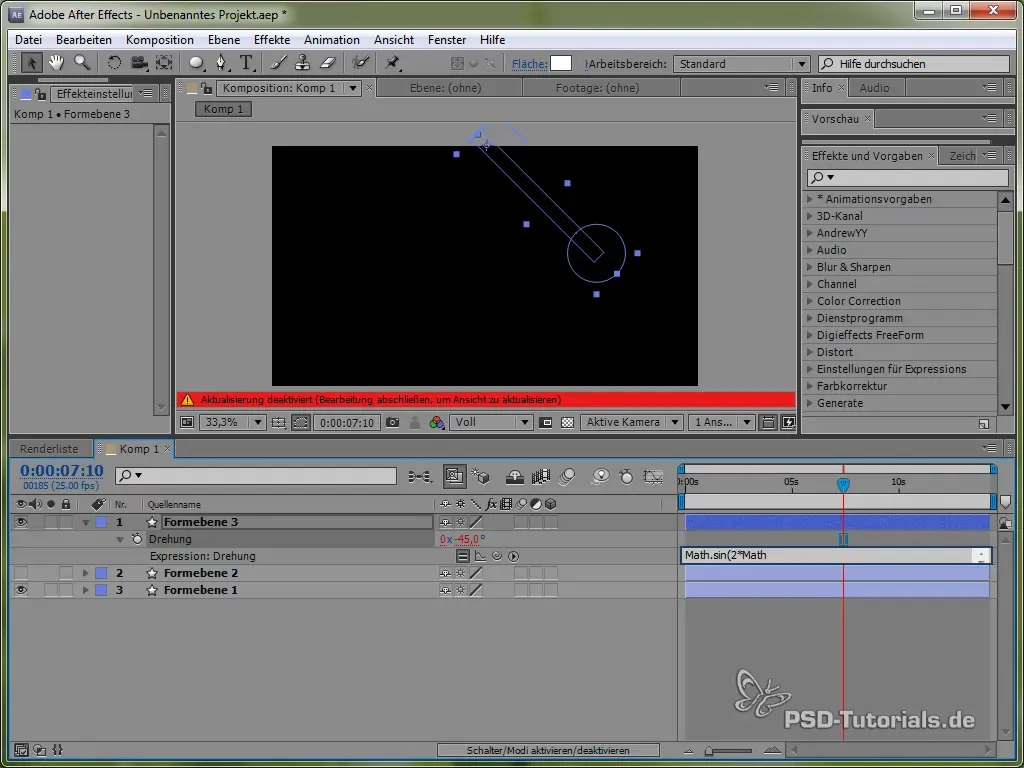
Avec le cosinus, nous commençons le processus d'oscillation à partir d'un point positif, ce qui est réaliste, car le pendule commence à osciller en haut.
Insérer des effets d'atténuation
Pour intégrer l'atténuation dans l'oscillation, nous utilisons la fonction exponentielle. Cela rend l'oscillation plus réaliste, car elle est forte au début puis diminue.
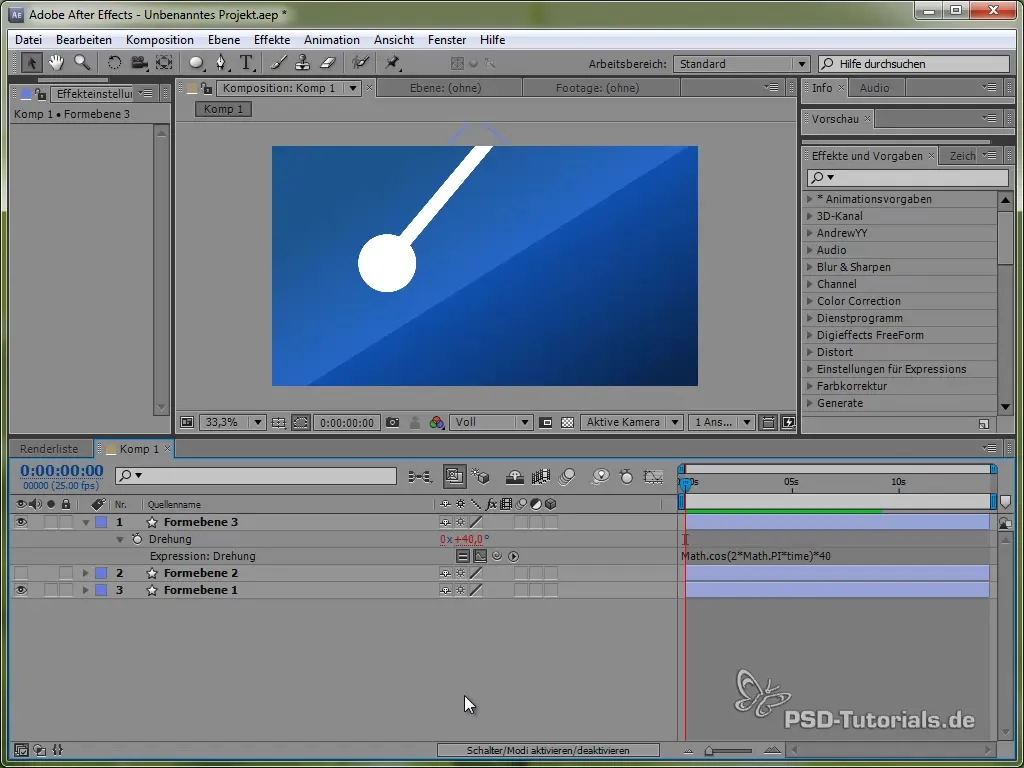
Un exemple de code pourrait être :
40 * Math.cos(2 * Math.PI * time) / Math.exp(time)
Ici, la division par la fonction exponentielle permet une atténuation lente.
Ajouter un effet de squash et stretch
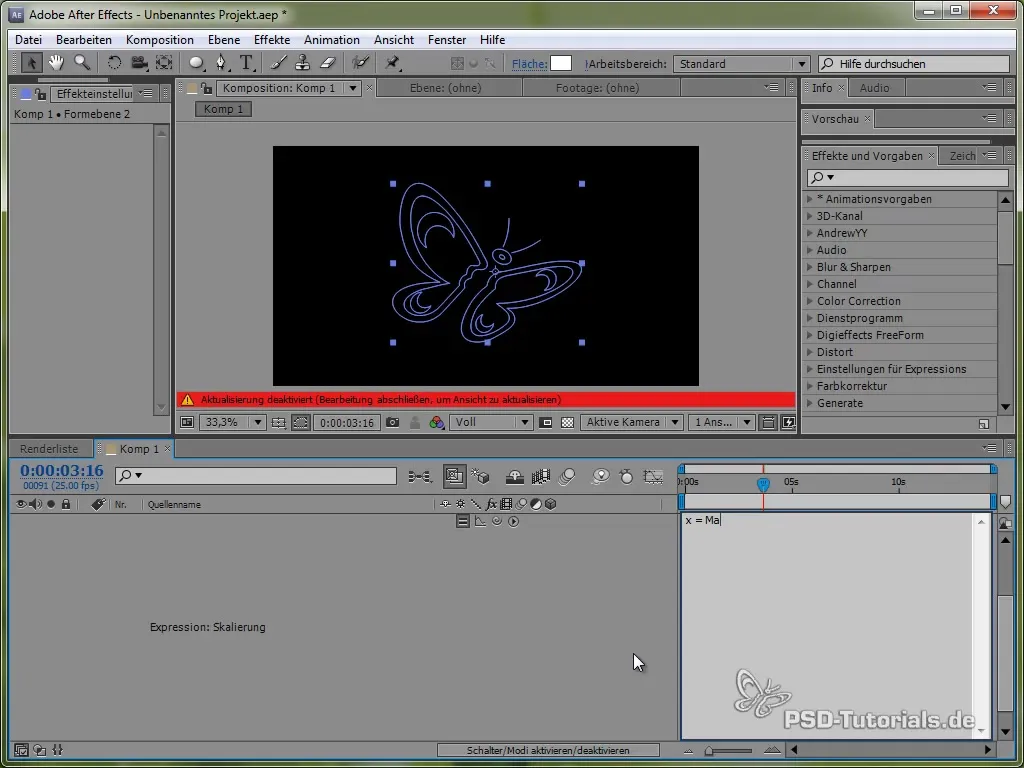
Pour des animations plus vivantes, tu peux également ajouter l'effet de squash and stretch. Tu peux faire cela en ajustant l'échelle du papillon.
Tu fais cela en appliquant une Expression à l'échelle qui peut être appliquée à la fois aux valeurs x et y en utilisant une fonction sinus ou cosinus.
Pensées finales
On voit qu'avec la bonne application des fonctions trigonométriques et exponentielles, il est possible de créer des animations très réalistes et intéressantes. Tu as appris à faire voler un papillon, à faire osciller un pendule et comment travailler avec des effets tels que le squash et stretch.
Résumé - Mathématiques dans les Expressions : Fonctions Trigonométriques & Exponentielles
Les mathématiques dans le contexte des Expressions dans After Effects t'ouvrent la possibilité de créer des animations créatives et vivantes. Les fonctions trigonométriques et exponentielles sont essentielles. Dans ce tutoriel, tu as acquis de l'expérience avec l'utilisation de ces concepts mathématiques dans la pratique.
Questions Fréquemment Posées
Comment ajouter une Expression dans After Effects ?Maintenez la touche ALT enfoncée et cliquez sur l'horloge à côté de la propriété pour laquelle vous souhaitez ajouter l'Expression.
Quelle est la différence entre les fonctions sinus et cosinus ?La fonction sinus commence à 0, tandis que la fonction cosinus commence à 1. Cela a un impact sur la manière dont les animations commencent.
Comment puis-je créer des effets d'atténuation ?Tu peux créer des effets d'atténuation en ajoutant des fonctions exponentielles à tes Expressions, qui réduisent le mouvement au fil du temps.


