Rekursija ir fundamentāls jēdziens informātikā un spēlē izšķirošu lomu sarežģītu problēmu risināšanā. Ja esi saskāries ar uzdevumiem, kuros problēma atkārto to pašu principu, noteikti esi dzirdējis par rekursiju. Neatkarīgi no tā, vai tas ir matemātiskos aprēķinos vai datu struktūrā, iespējas ir daudzveidīgas. Šajā rokasgrāmatā mēs runāsim īpaši par rekursīvā metode izveidi Java valodā, lai aprēķinātu skaitļa faktoriālu. Sāksim soli pa solim saprast, kā efektīvi izmantot rekursiju.
Galvenās atziņas
- Rekursija ir pašreferenciāls zvans
- Katrai rekursīvai metodei ir nepieciešama izbeigšanas nosacījums
- Faktoriāla aprēķināšanā problēma tiek sadalīta mazākos apakšproblēmās
Soli pa solim rokasgrāmata faktoriāla aprēķināšanas ieviešanai
Lai izveidotu rekursīvo metodi, sāksim ar pamatiem. Skaitļa n faktoriāls (n!) ir visu pozitīvo veselo skaitļu produkts līdz n. Piemēram, skaitļa 3 faktoriāls (3!) ir 1 × 2 × 3 = 6.
1. Metodes definīcija
Vispirms mums jādefinē metode, kas aprēķina faktoriālu. Mēs izmantosim atgriešanas tipu long, lai efektīvi apstrādātu lielākus skaitļus.
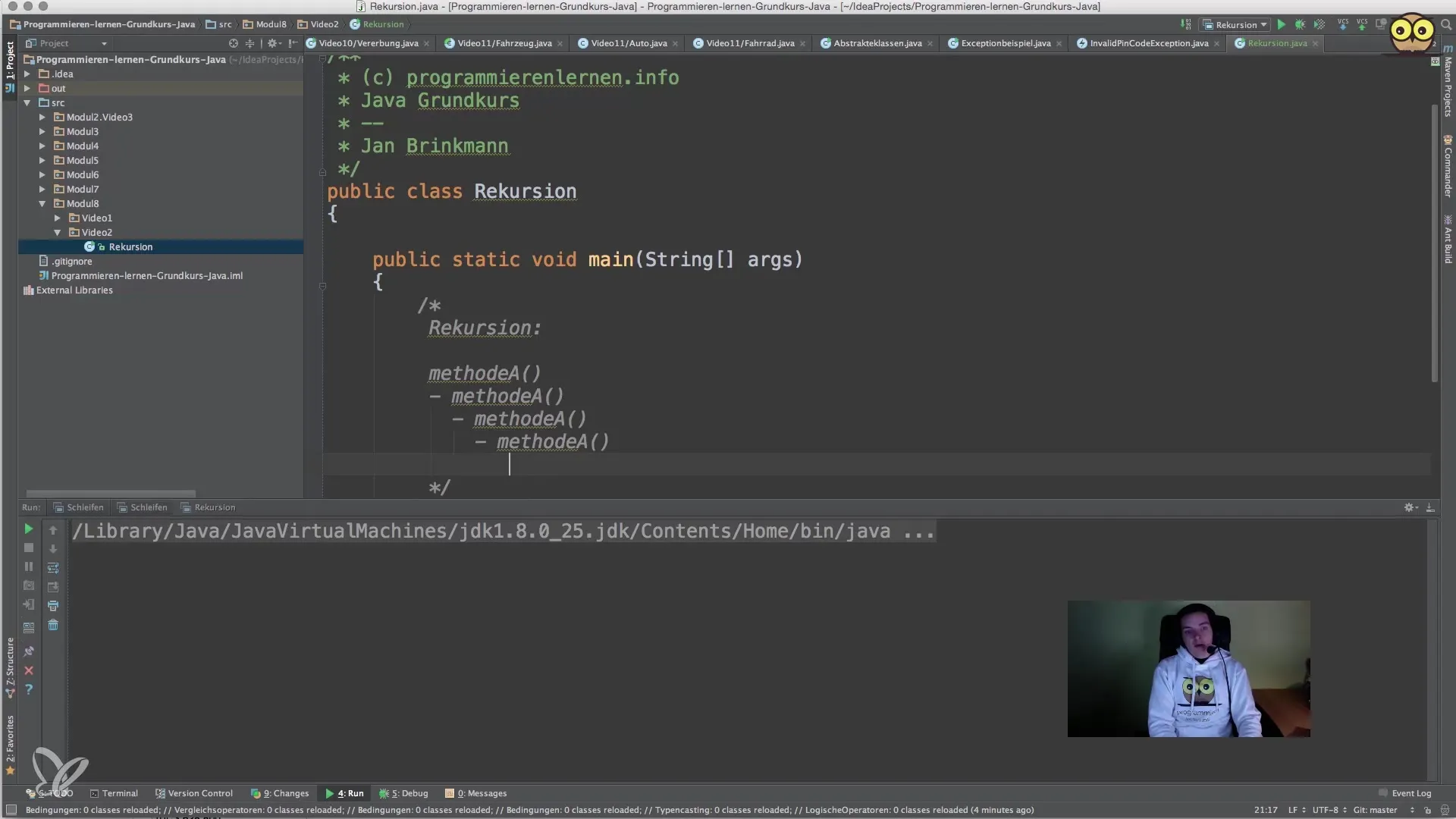
Metode tiek deklarēta kā statiska, jo mēs vēlamies to izsaukt no galvenās metodes.
Šajā rindā tu jau esi izveidojis šablonu savai metodei.
2. Izbeigšanas nosacījums
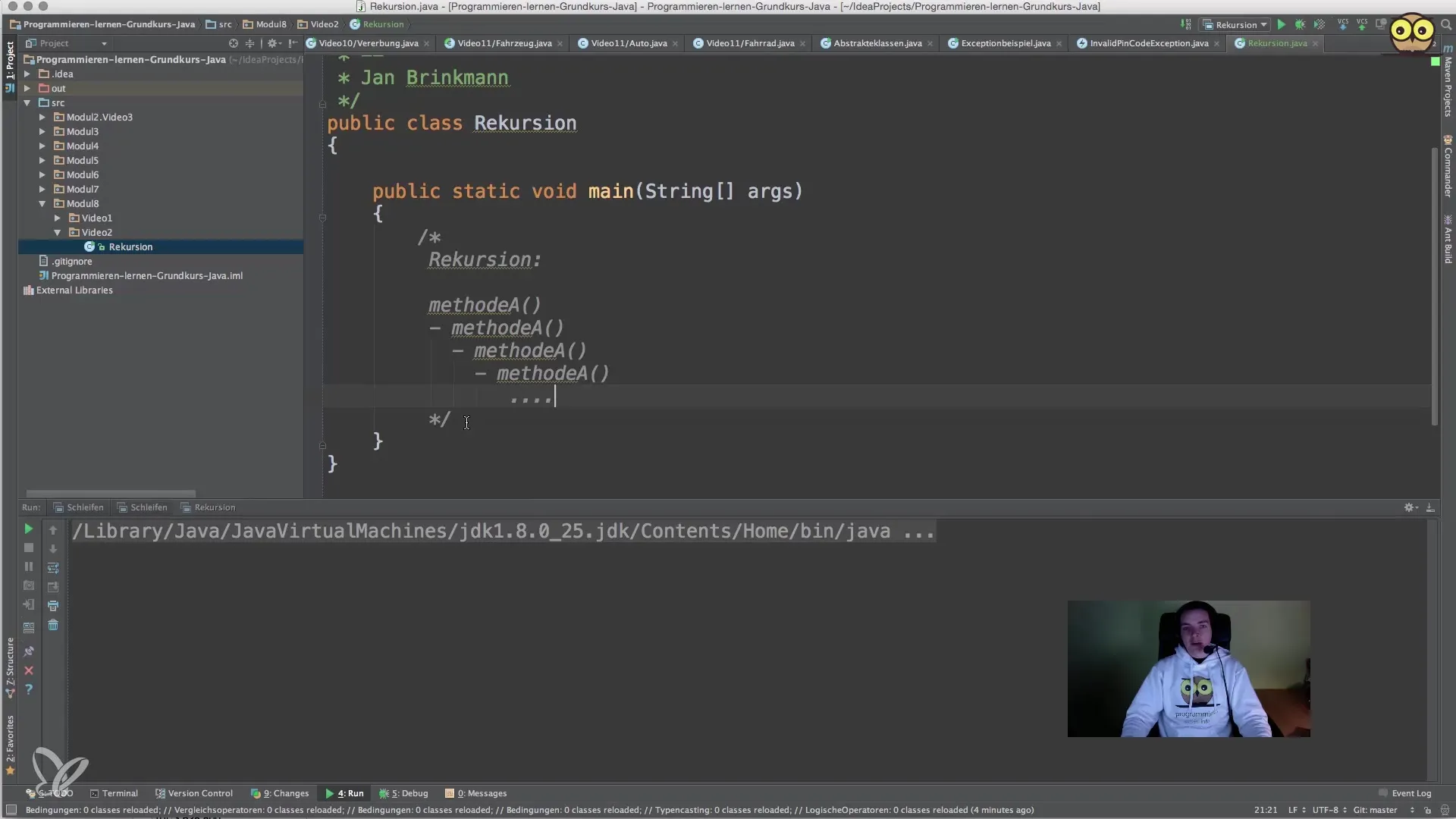
Izšķirošs elements rekursīvajā metodē ir izbeigšanas nosacījums. Tam ir jānodrošina, ka rekursija nebeidzas. Faktoriāla aprēķināšanā izbeigšanas nosacījums ir tas, ka mēs aprēķinām faktoriālu no 0 vai 1, kas abiem ir vērtība 1.
Šī rinda informē metodi, ka tā var nekavējoties pabeigt aprēķinu pie 0 vai 1.
3. Rekursīvais zvans
Tagad seko mūsu metodes galvenā daļa – rekursīvais zvans. Šeit mēs izsaucam mūsu metodi pašā metodē, taču ar samazinātu vērtību.
Tas nozīmē, ka mēs reizinām pašreizējo skaitli ar faktoriālu skaitlim, kas samazināts par vienu.
4. Pilnīgs kods
Tagad mēs apvienojam visus elementus un redzam, kā izskatās mūsu metode.
5. Metodes izsaukums
Mēs tagad izsaucam mūsu metodi galvenajā metodē, lai pārbaudītu, vai viss darbojas.
6. Testēšana un rezultātu pārbaude
Ja tu tagad palaidīsi programmu, tai vajadzētu izvadīt faktoriālu no 3: 6.
Ir svarīgi, lai tu pārbaudītu rezultātu, lai pārliecinātos, ka viss darbojas pareizi.
7. Debuggeru izmantošana
Es iesaku tev izmantot debuggeru, lai labāk izprastu rekursijas procesu. Soli pa solim iziešana parāda, kā vērtības tiek nodotas vairāku izsaukumu laikā.
Tu vari novērot, kā metode tiek rekursīvi izsaukta, kas palīdzēs tev saprast rekursijas pamatloģiku.
Apkopojums – Rekursija Java valodā – Efektīvas metodes ar pašreferenci
Rekursijas izmantošana sākumā var būt izaicinoša, tomēr tā piedāvā efektīvu veidu, kā risināt sarežģītas problēmas. Šajā rokasgrāmatā tu esi mācījies, kā ieviešot rekursīvu metodi faktoriāla aprēķināšanai Java valodā. Mēs esam apskatījuši svarīgus jēdzienus, piemēram, izbeigšanas nosacījumu un rekursīvo loģiku.
Bieži uzdotie jautājumi
Kas ir rekursija?Rekursija ir metode, kurā funkcija izsauc sevi, lai risinātu problēmu.
Kāpēc ir nepieciešams izbeigšanas nosacījums?Izbeigšanas nosacījums novērš funkcijas bezgalīgu izsaukumu, kas var izraisīt steka pārslogošanu.
Kā aprēķina skaitļa faktoriālu?Skaitļa n (n!) faktoriāls ir visu pozitīvo veselo skaitļu produkts no 1 līdz n.


