Wiskunde in Expressies: Trigonometriche & Exponentiële Concepten

Wiskunde speelt een fundamentele rol in de digitale wereld en vooral in videobewerking met After Effects (AE) opent het geheel nieuwe mogelijkheden. In deze tutorial leer je hoe je trigonometrische en exponentiële functies in AE kunt gebruiken als Expressions om fascinerende animaties te creëren. Een bijzonder spannend voorbeeld zal de beweging van een vlinder zijn, die je laat zien hoe fysieke simulaties met behulp van wiskunde kunnen worden gerealiseerd.

Belangrijkste bevindingen

• Trigonometrische functies zoals sinus en cosinus kunnen worden gebruikt om verschoven bewegingen te genereren.
• Exponentiële functies worden gebruikt om dempingseffecten te simuleren.
• Het gebruik van absolute waarden in functies kan helpen om bepaalde animatie-effecten te bereiken.

Stapsgewijze handleiding

Vlinder in beweging brengen

Om onze vlinder in beweging te brengen, moet je hem eerst zo animeren dat hij zich in een golfbeweging verplaatst. Deze golfbeweging kan zonder veel moeite via Expressions worden gerealiseerd.

Begin door de positie van de vlinder te openen door op de toets „P“ te drukken. Zet vervolgens een Expression voor de positie door de ALT-toets in te drukken en op de klok te klikken.

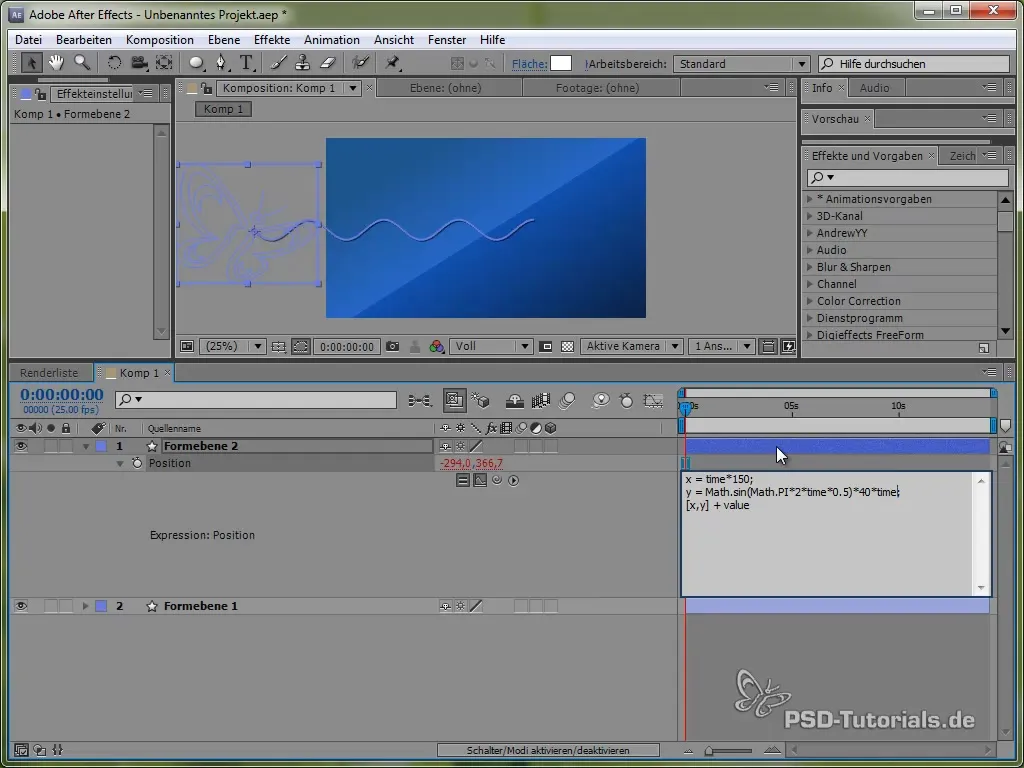
Hiervoor gebruiken we eerst de tijdvariabele time, vermenigvuldigd met een waarde die de snelheid van de beweging vastlegt. Bijvoorbeeld:

value[0] + time * 150

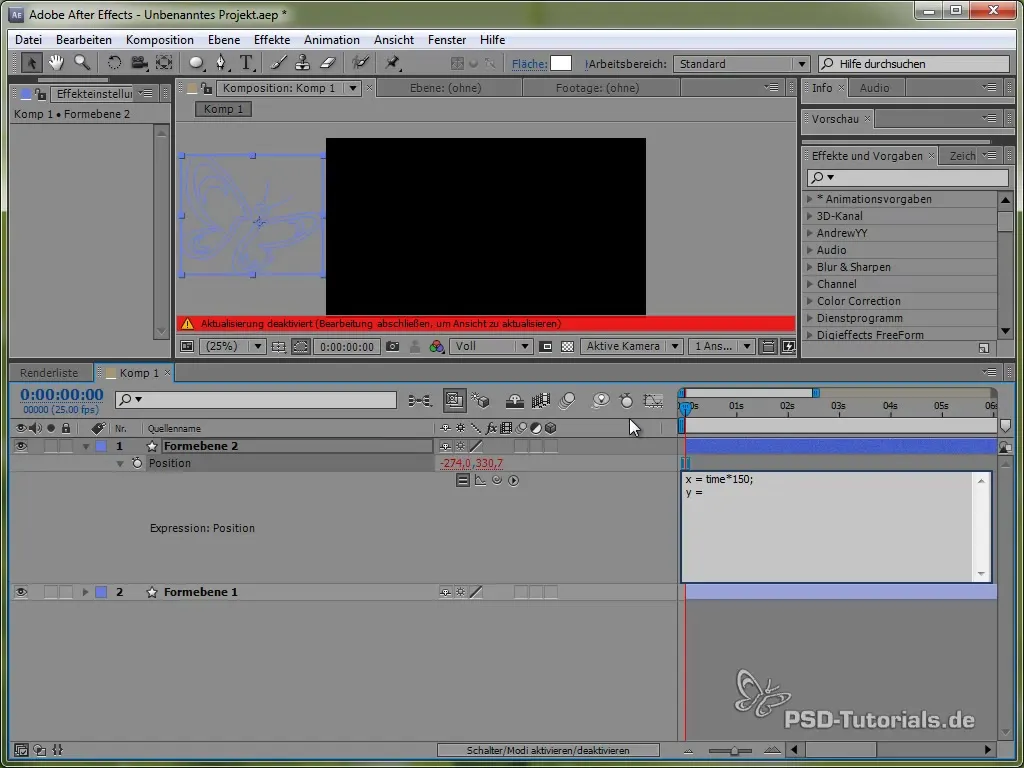
Deze code zorgt ervoor dat de vlinder zich in de X-richting constant met 150 pixel per seconde beweegt. Voor de Y-richting zullen we een sinusfunctie gebruiken die de verticale beweging van de vlinder genereert en deze tussen bepaalde waarden "laat wiegen".

Toepassing van de sinusfunctie

De Y-beweging wordt gedefinieerd door de volgende Expression:

value[1] + 40 * Math.sin(2 * Math.PI * time)

Hierbij zet Math.sin() de sinusfunctie om. Het varieert tussen -1 en 1 en wordt met 40 vermenigvuldigd, wat betekent dat de vlinder in de Y-richting tussen -40 en 40 pixels wiegt.

Bewegingsgrafiek visualiseren

Om deze beweging beter te visualiseren, kun je het grafiekvenster in After Effects activeren. Dit toont je de fluctuaties van de sinuswaarde duidelijker.

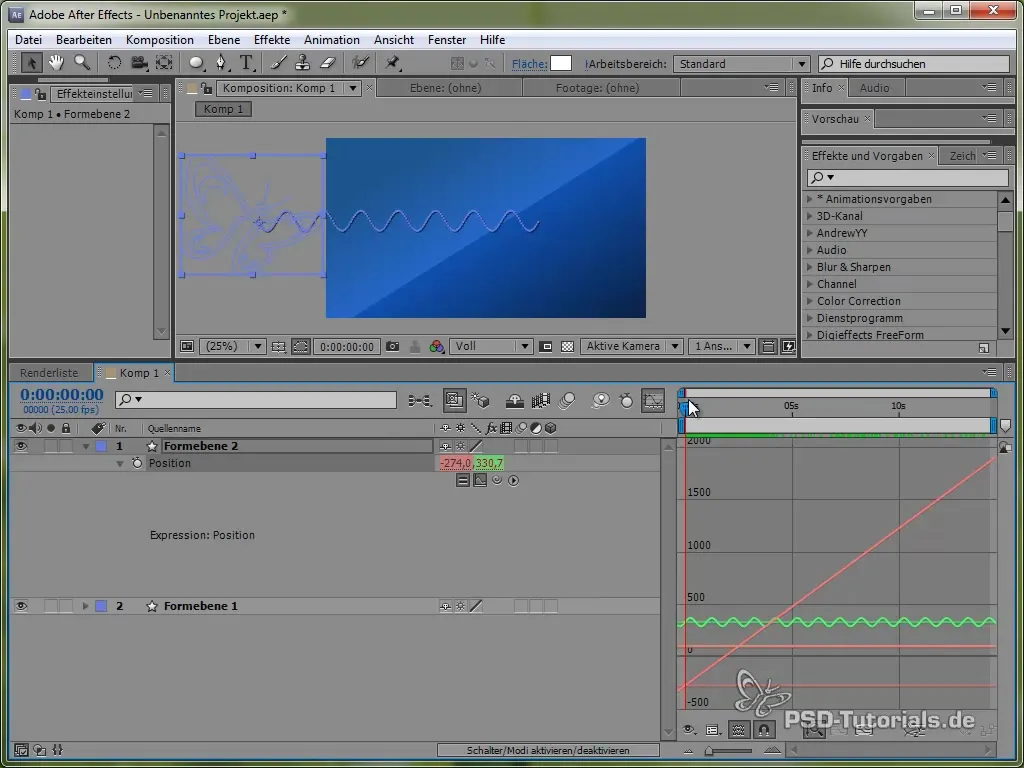
Je ziet dat het signaal oscilleert en zich over het scherm verplaatst.

Amplitude en frequentie variëren

Nu kun je de amplitude aanpassen om verschillende sterkte van fluctuaties te genereren. Als je bijvoorbeeld de amplitude in de tijd wilt verhogen, kun je het volgende gebruiken:

40 * (time * 10) * Math.sin(2 * Math.PI * time)

Dit zorgt ervoor dat de amplitude in de loop van de tijd stijgt, wat betekent dat de vlinder na een seconde met 40 pixels wiegt, na twee seconden met 80 pixels, en ga zo maar door.

Een pendel maken

Om de omgang met verschillende fysieke simulaties te verdiepen, richten we ons nu op het maken van een pendel. Teken eerst een dunne staaf en voeg een ellips aan het einde toe.

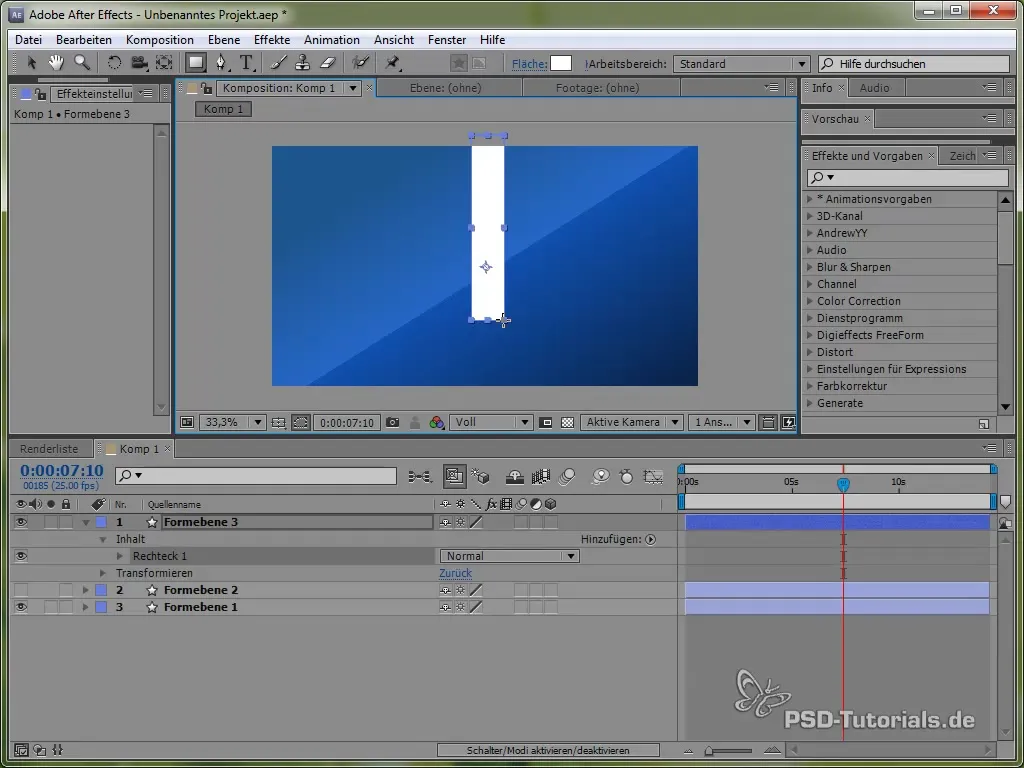
Positioneer het ankerpunt bovenaan de pendel, zodat deze kan zwaaien. Dit gebeurt met het ankerpunt-gereedschap.

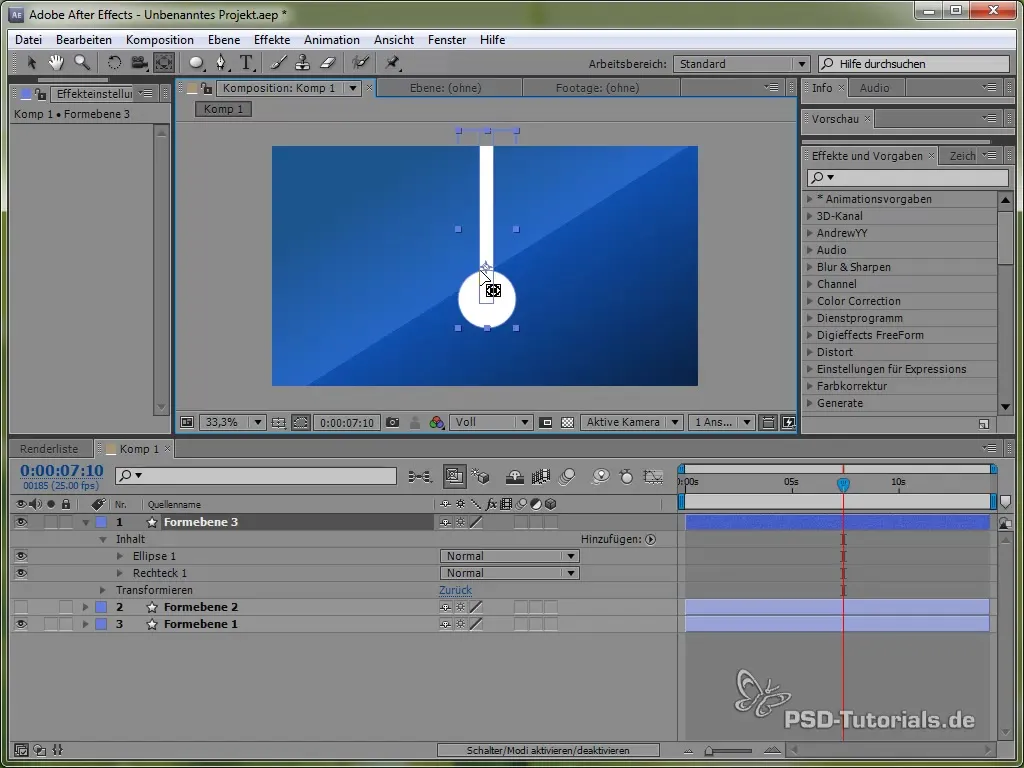
Zet vervolgens de Expression:

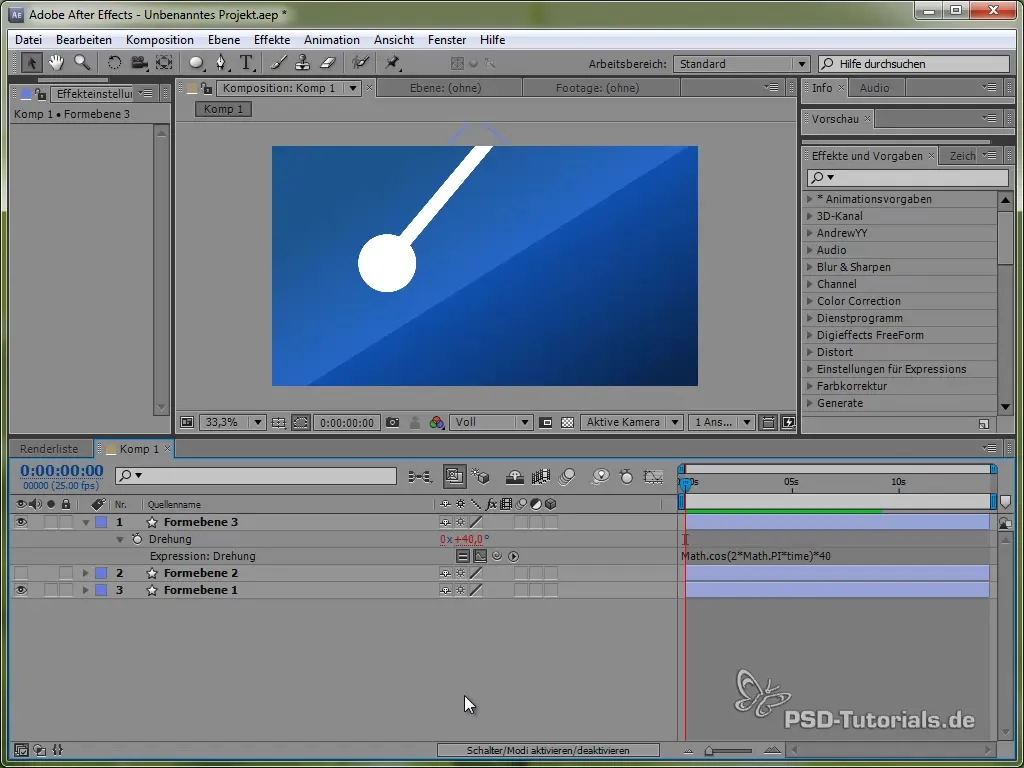
value + 40 * Math.cos(2 * Math.PI * time)

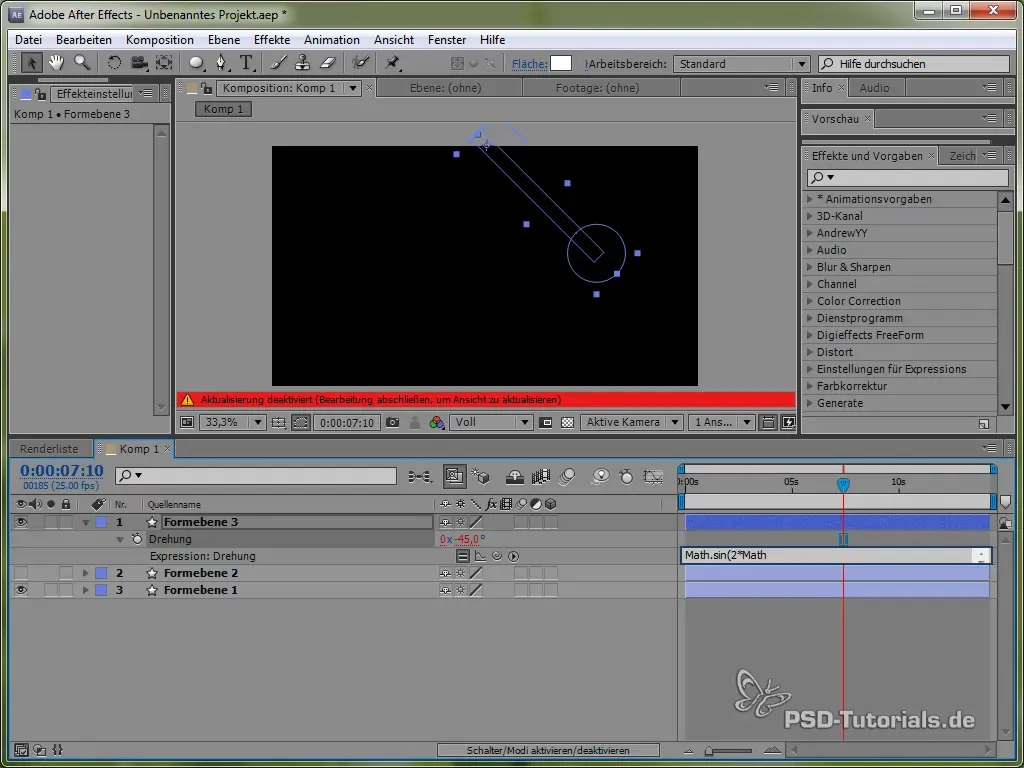
Door de cosinus starten we het zwaaiproces vanaf een positief punt, wat realistisch is, omdat de pendel bovenaan begint te bewegen.

Dempingseffecten toevoegen

Om demping in de oscillatie te integreren, gebruiken we de exponentiële functie. Hierdoor lijkt de oscillatie realistischer, omdat ze in het begin sterk is en uiteindelijk afneemt.

Een voorbeeldcode kan er als volgt uitzien:

40 * Math.cos(2 * Math.PI * time) / Math.exp(time)

Hierbij zorgt de deling door de exponentiële functie voor een langzame demping.

Squash en Stretch toevoegen

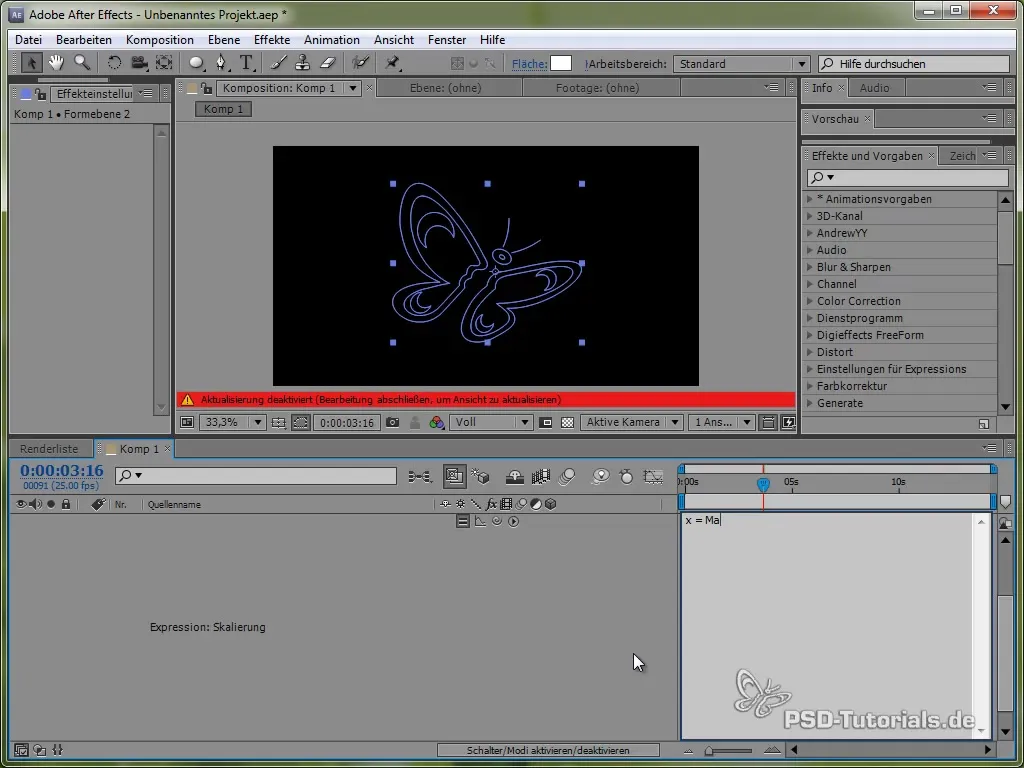
Voor levendigere animaties kun je ook het Squash and Stretch-effect toevoegen. Dit kun je bereiken door de schaal van de vlinder aan te passen.

Je doet dit door een Expression toe te passen op de schaalwaarde, die zowel op x- als op y-waarden kan worden toegepast, waarbij je een sinus- of cosinusfunctie gebruikt.

Eindgedachten

Je ziet dat door de juiste toepassing van trigonometrische en exponentiële functies zeer realistische en interessante animaties kunnen worden gemaakt. Je hebt geleerd hoe je een vlinder kunt laten vliegen, een pendel kunt laten zwaaien en hoe je met effecten zoals Squash and Stretch kunt werken.

Samenvatting - Wiskunde in Expressions: Trigonometrische & Exponentiële Functies

Wiskunde in de context van Expressions in After Effects biedt je de mogelijkheid om creatieve en levendige animaties te creëren. Trigonometrische en exponentiële functies zijn daarbij essentieel. In deze tutorial heb je ervaring opgedaan met het gebruik van deze wiskundige concepten in de praktijk.