Matematik spiller en fundamental rolle i den digitale verden, og især i videoredigering med After Effects (AE) åbner den helt nye muligheder for dig. I denne vejledning vil du lære, hvordan du kan bruge trigonometriske og eksponentielle funktioner i AE som Expressions for at skabe fascinerende animationer. Et særligt spændende eksempel vil være bevægelsen af en sommerfugl, som viser dig, hvordan fysiske simulationer kan implementeres ved hjælp af matematik.
Vigtigste indsigter
- Trigonometriske funktioner som sinus og cosinus kan bruges til at skabe forskudte bevægelser.
- Eksponentielle funktioner bruges til at simulere dæmpningseffekter.
- Brugen af absolutte værdier i funktioner kan hjælpe med at opnå bestemte animationseffekter.
Trin-for-trin vejledning
Bevæg sommerfuglen
For at få vores sommerfugl til at bevæge sig, skal du først animere den, så den bevæger sig i en bølge. Denne bølgebevægelse kan realiseres uden store anstrengelser ved hjælp af Expressions.
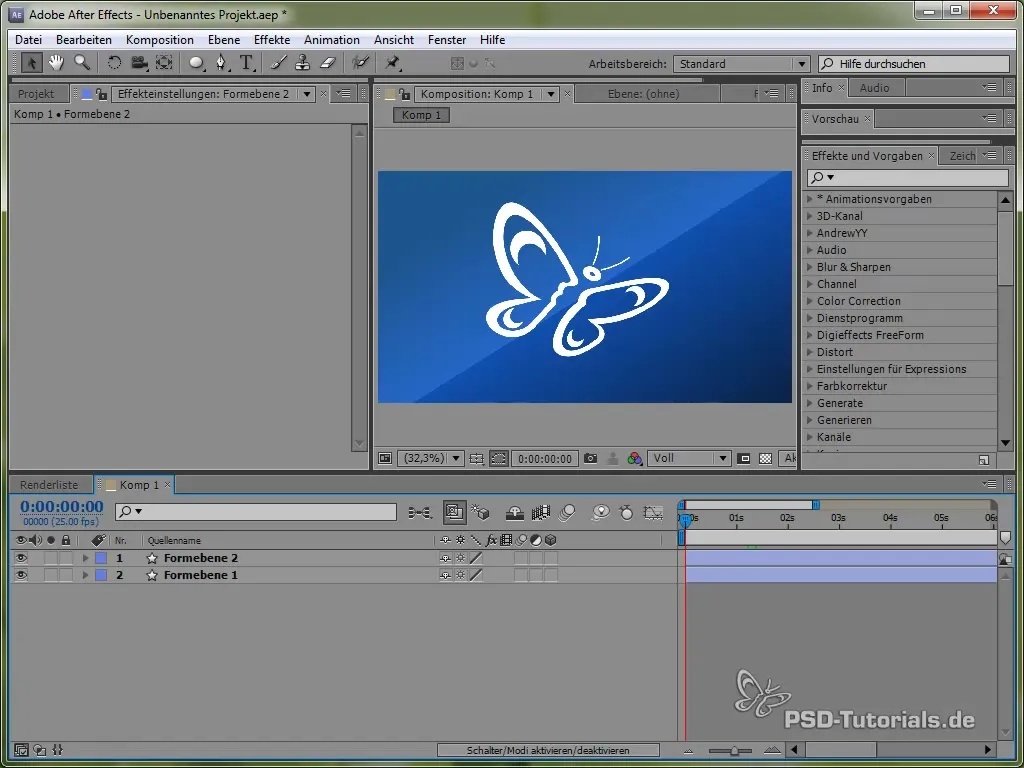
Begynd med at åbne positionen for sommerfuglen ved at trykke på tasten „P“. Sæt derefter en Expression for positionen ved at holde ALT-tasten nede og klikke på uret.
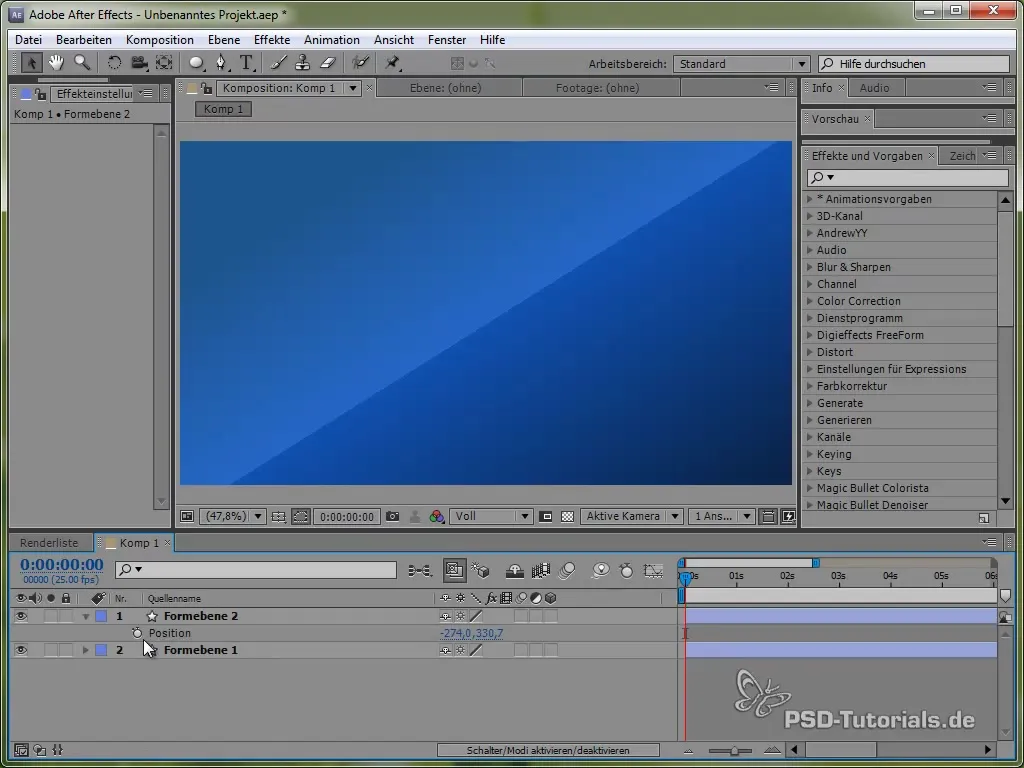
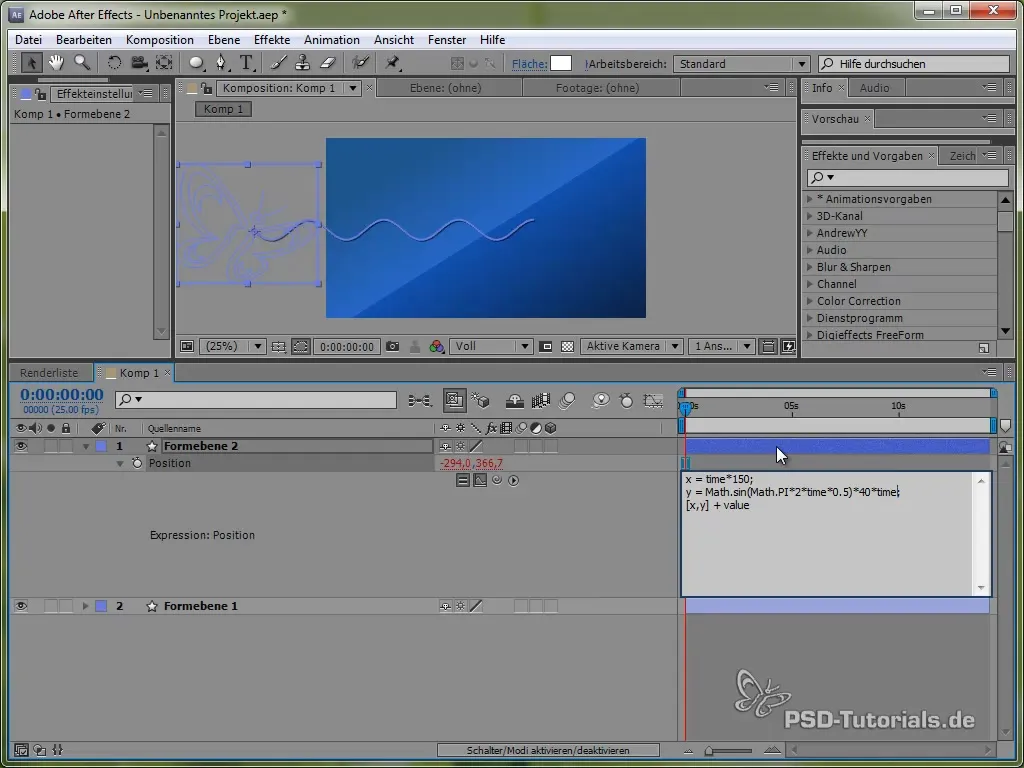
Til dette bruger vi først tidsvariablen time, multipliceret med en værdi, der bestemmer bevægelsens hastighed. For eksempel:
value[0] + time * 150
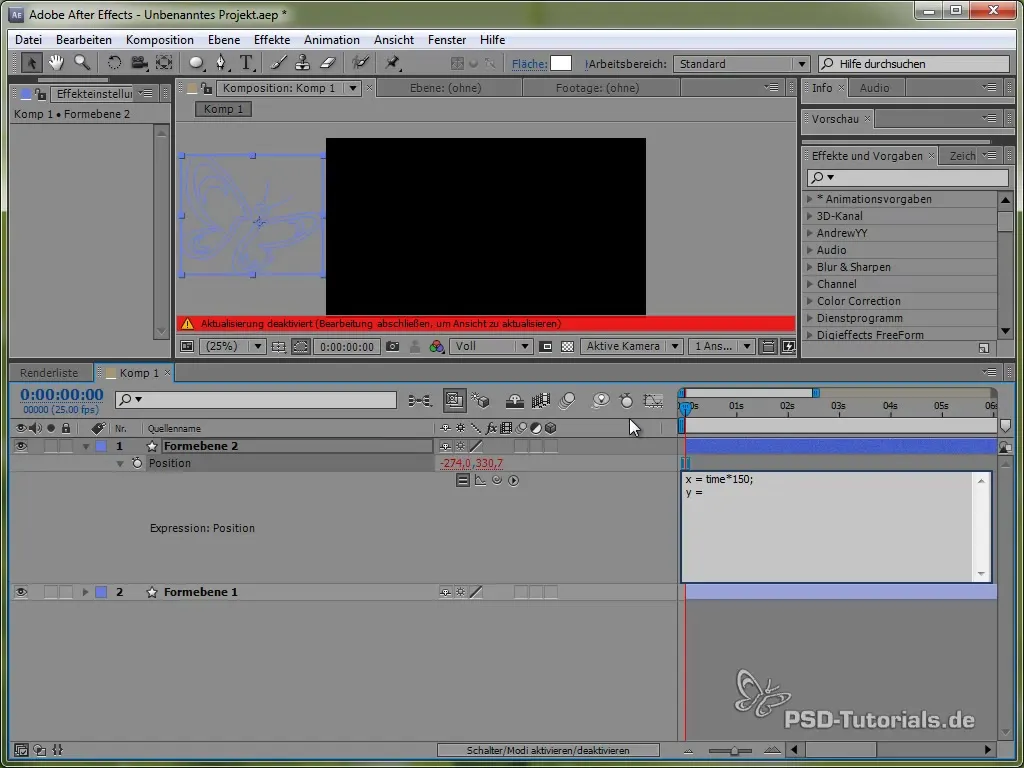
Denne kode får sommerfuglen til at bevæge sig konstant med 150 pixels pr. sekund i X-retningen. For Y-retningen vil vi bruge en sinusfunktion, der skaber den vertikale bevægelse af sommerfuglen og får den til at „svinge“ mellem bestemte værdier.
Anvendelse af sinusfunktionen
Y-bevægelsen defineres ved følgende Expression:
value[1] + 40 * Math.sin(2 * Math.PI * time)
Her anvender Math.sin() sinusfunktionen. Den varierer mellem -1 og 1 og multipliceres med 40, hvilket betyder, at sommerfuglen svinger mellem -40 og 40 pixels i Y-retningen.
Visualisere bevægelseskurven
For bedre at visualisere denne bevægelse kan du aktivere grafikvinduet i After Effects. Dette viser dig ændringerne i sinusværdien tydeligere.
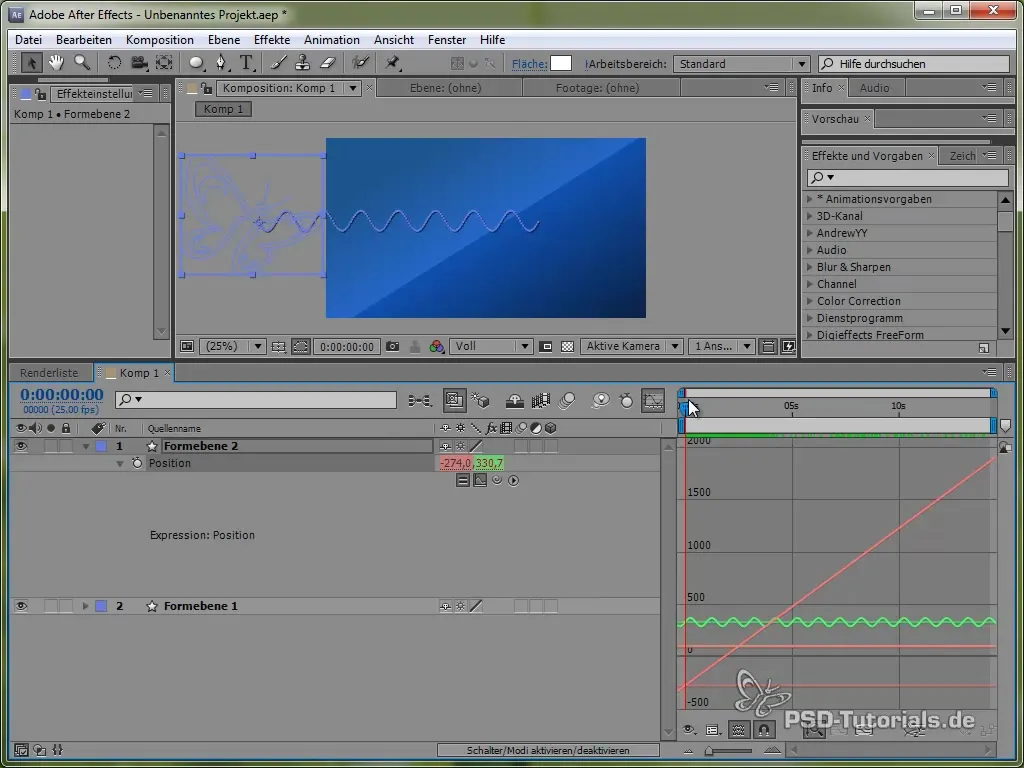
Man kan se, at signalet oscillerer og bevæger sig over skærmen.
Variere amplitude og frekvens
Nu kan du justere amplituden for at skabe forskellige stærke svigning. Hvis du for eksempel ønsker at øge amplituden over tid, kan du bruge følgende:
40 * (time * 10) * Math.sin(2 * Math.PI * time)
Derved vil amplituden stige med tiden, hvilket får sommerfuglen til at svinge 40 pixels efter et sekund, 80 pixels efter to sekunder og så videre.
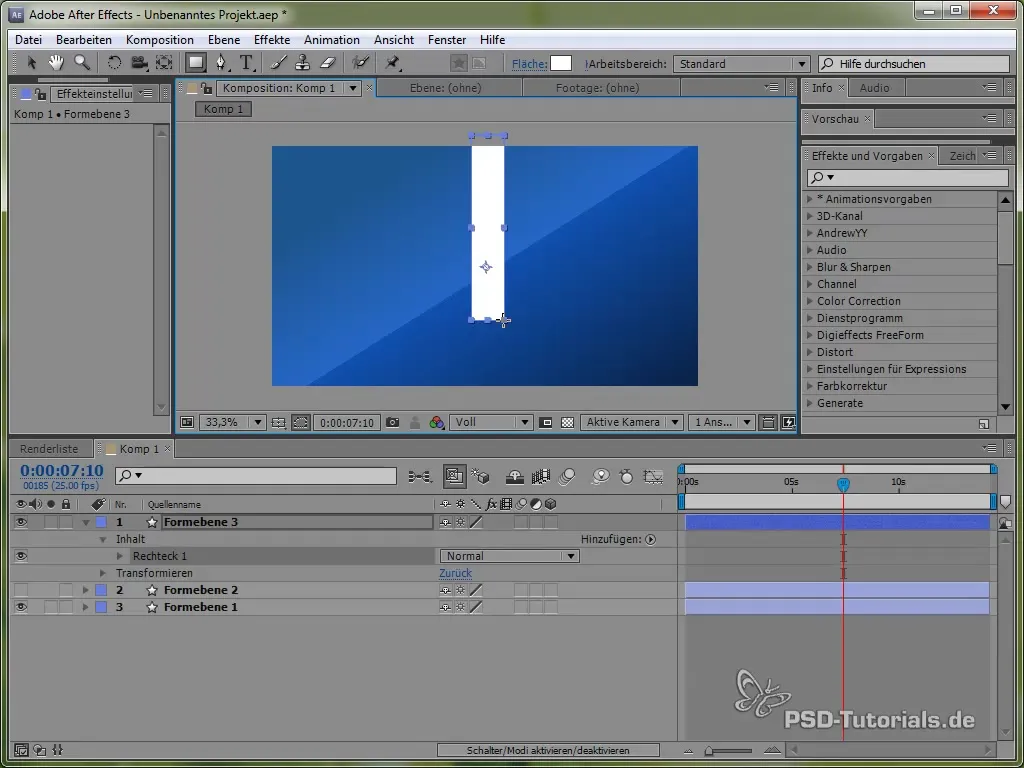
Opret et pendul
For at dykke dybere ned i håndteringen af forskellige fysiske simulationer, vil vi nu skabe et pendul. Tegn først en tynd stang og tilføj en ellipse i enden af den.
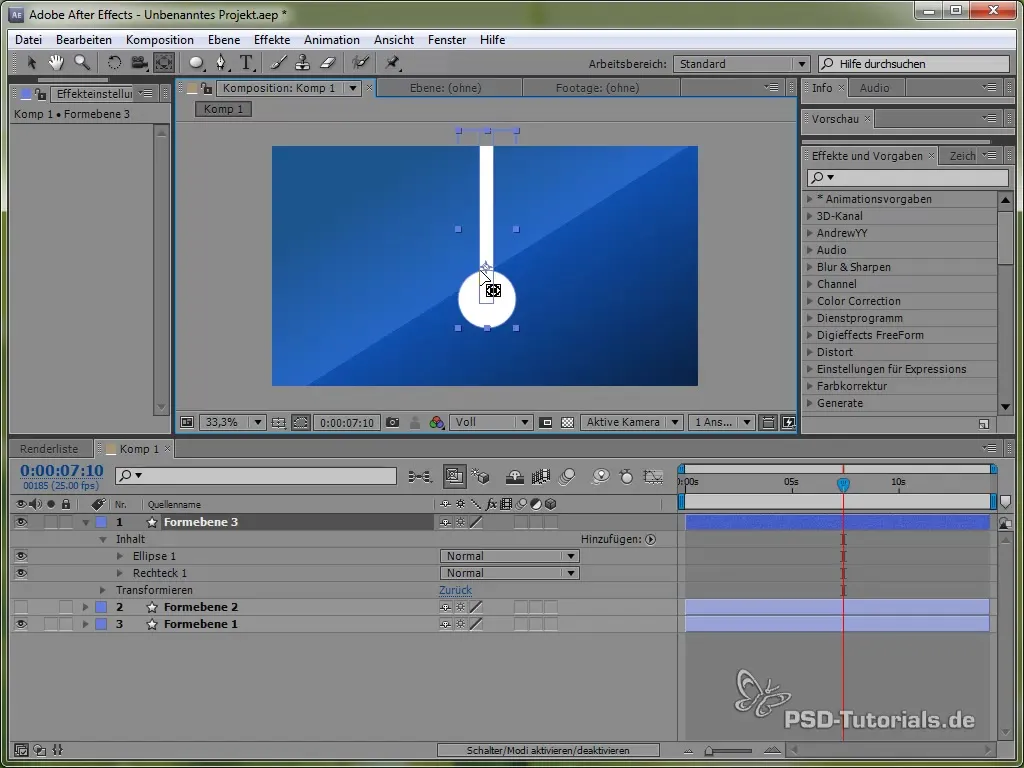
Positioner ankerpunktet øverst på pendulet, så det kan svinge. Dette gøres med ankerpunktsværktøjet.
Sæt derefter følgende Expression:
value + 40 * Math.cos(2 * Math.PI * time)
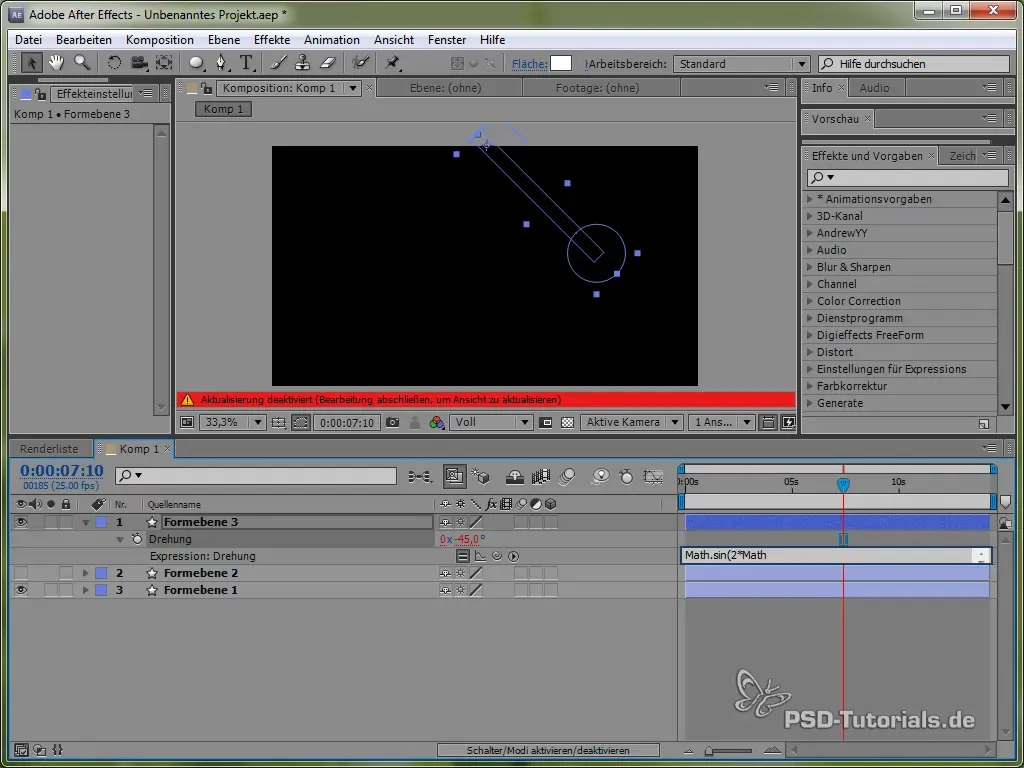
Ved hjælp af cosinus starter vi svingningsprocessen fra et positivt punkt, hvilket er realistisk, da pendulet begynder at svinge ovenfra.
Indsæt dæmpningseffekter
For at integrere dæmpning i svingningen bruger vi den eksponentielle funktion. Dette gør svingningen mere realistisk, da den er kraftig i starten og gradvist svinder bort.
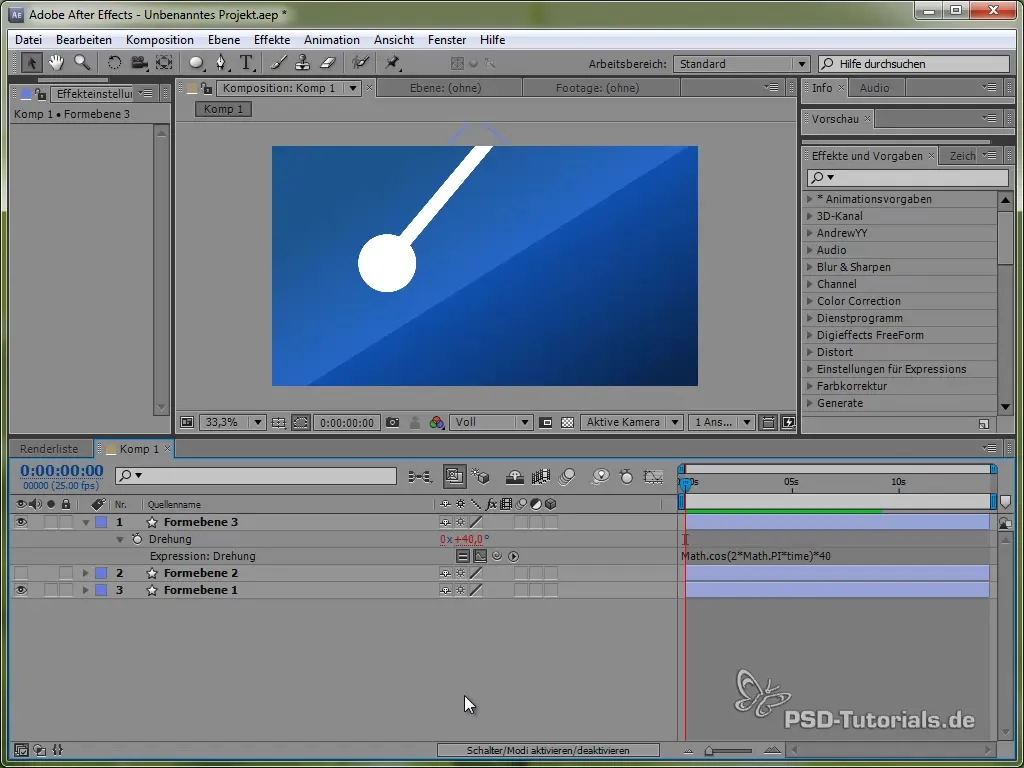
Et eksempel på koden kunne se således ud:
40 * Math.cos(2 * Math.PI * time) / Math.exp(time)
Her sørger divisionen med eksponentialfunktionen for en langsom dæmpning.
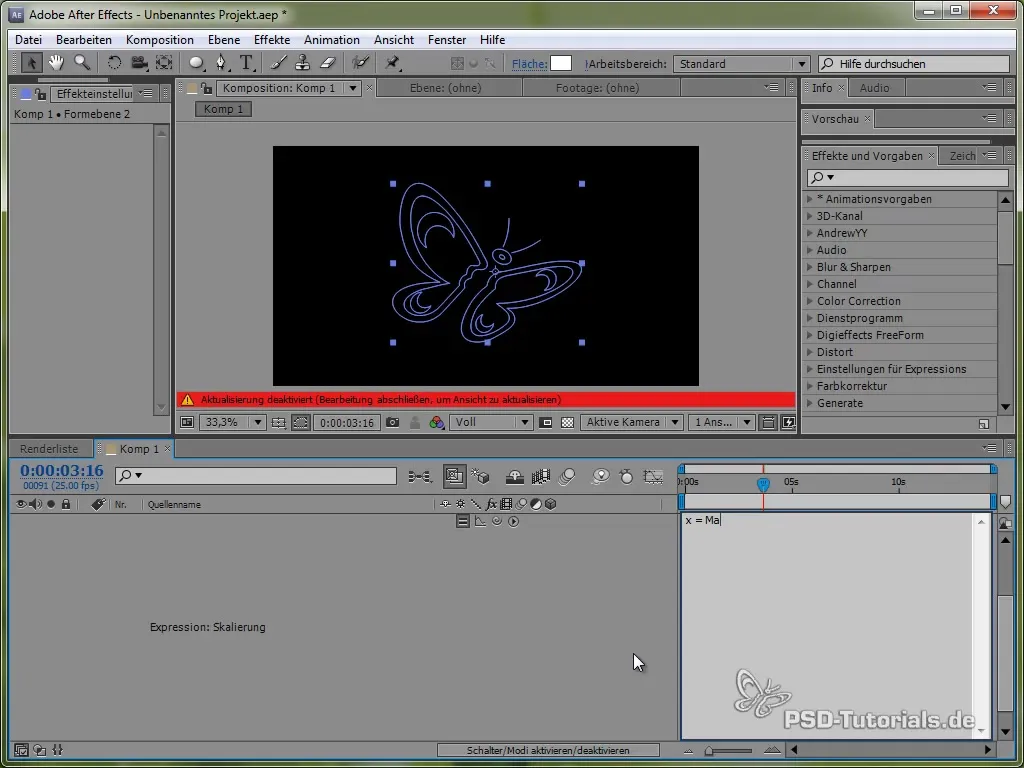
Tilføj squash og stretch
For mere livlige animationer kan du også tilføje squash and stretch-effekten. Dette kan du opnå gennem skaleringsfunktionerne på sommerfuglen.
Du gør dette ved at anvende en Expression på skaleringsværdien, som kan anvendes både på x- og y-værdier ved hjælp af en sinus- eller cosinusfunktion.
Afsluttende tanker
Man ser, at ved korrekt anvendelse af trigonometriske og eksponentielle funktioner, kan der skabes meget realistiske og interessante animationer. Du har lært, hvordan man får en sommerfugl til at flyve, får et pendul til at svinge, og hvordan man arbejder med effekter som squash og stretch.
Opsummering - Matematik i Expressions: Trigonometriske & Eksponentielle funktioner
Matematik i konteksten af Expressions i After Effects giver dig mulighed for at skabe kreative og livlige animationer. Trigonometriske og eksponentielle funktioner er essentielle her. I denne vejledning har du fået erfaring med brugen af disse matematiske koncepter i praksis.
Ofte stillede spørgsmål
Hvordan anvender jeg en Expression i After Effects?Hold ALT-tasten nede og klik på uret ved siden af den egenskab, som du ønsker at tilføje Expression til.
Hvad er forskellen mellem sinus- og cosinusfunktioner?Sinusfunktionen starter ved 0, mens cosinusfunktionen starter ved 1. Dette har indflydelse på, hvordan animationer starter.
Hvordan kan jeg skabe dæmpningseffekter?Du kan skabe dæmpningseffekter ved at indsætte eksponentielle funktioner i dine Expressions, der reducerer bevægelsen over tid.


