Матhematics відіграє фундаментальну роль у цифровому світі, а особливо в редагуванні відео за допомогою After Effects (AE), відкриваючи тобі зовсім нові можливості. У цьому навчальному посібнику ти дізнаєшся, як ти можеш використовувати тригонометричні та експоненціальні функції в AE як висловлювання, щоб створювати захоплюючі анімації. Особливо цікавим прикладом буде рух метелика, який покаже, як фізичні симуляції можуть бути реалізовані за допомогою математики.
Найважливіші висновки
- Тригонометричні функції, такі як синус і косинус, можна використовувати для створення зміщених рухів.
- Експоненціальні функції використовуються для симуляції гасіння ефектів.
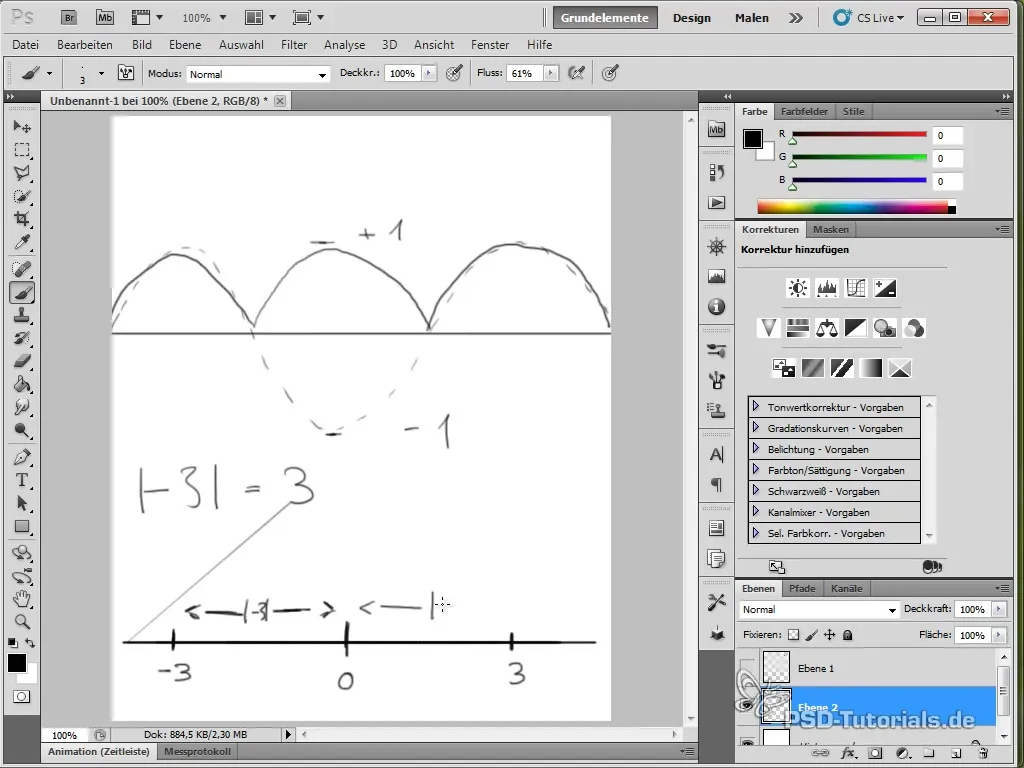
- Використання абсолютних значень у функціях може допомогти досягти певних анімаційних ефектів.
Покрокова інструкція
Рух метелика
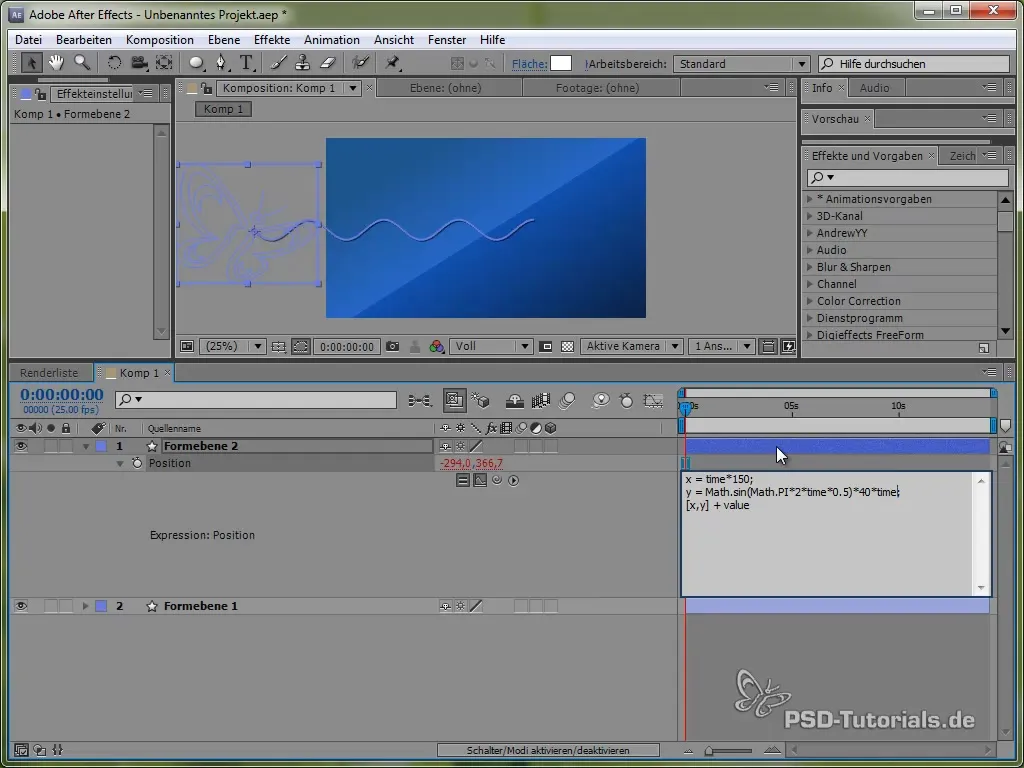
Щоб навести метелика в рух, спочатку потрібно анімувати його так, щоб він рухався у хвилі. Цей хвилеподібний рух можна реалізувати без особливих зусиль за допомогою висловлювань.
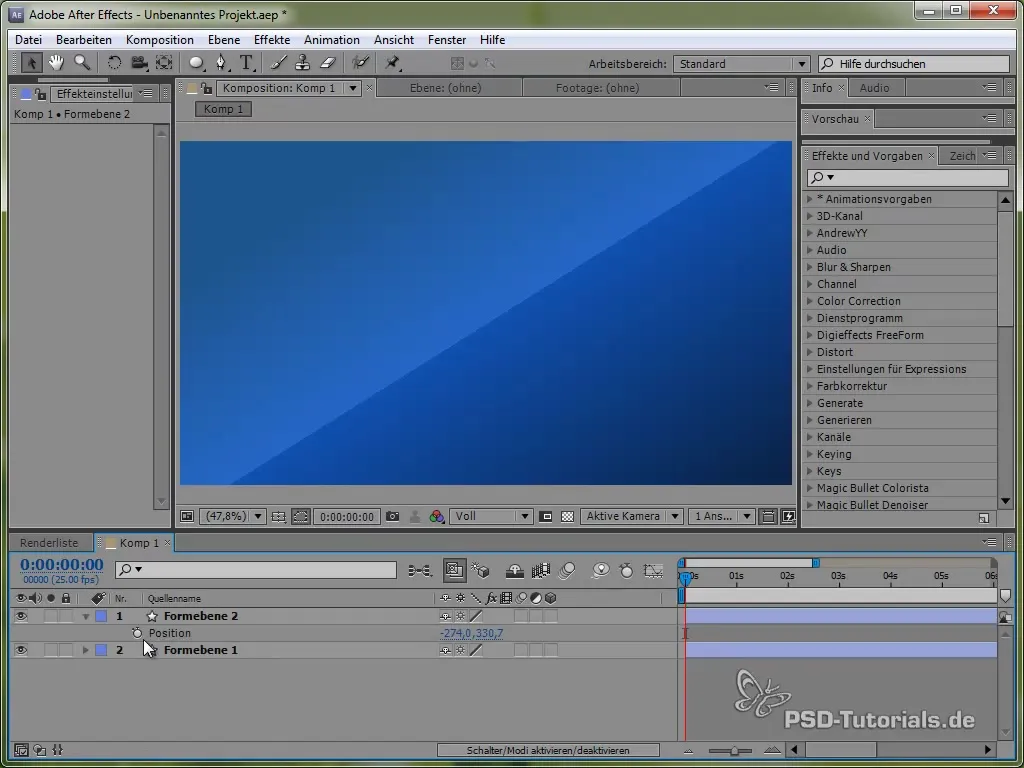
Почни з того, щоб відкрити позицію метелика, натиснувши клавішу «P». Потім встанови висловлення для позиції, натиснувши клавішу ALT і клікнувши на годинник.
Для цього спочатку використовуємо змінну часу time, помножену на значення, яке визначає швидкість руху. Наприклад:
value[0] + time * 150
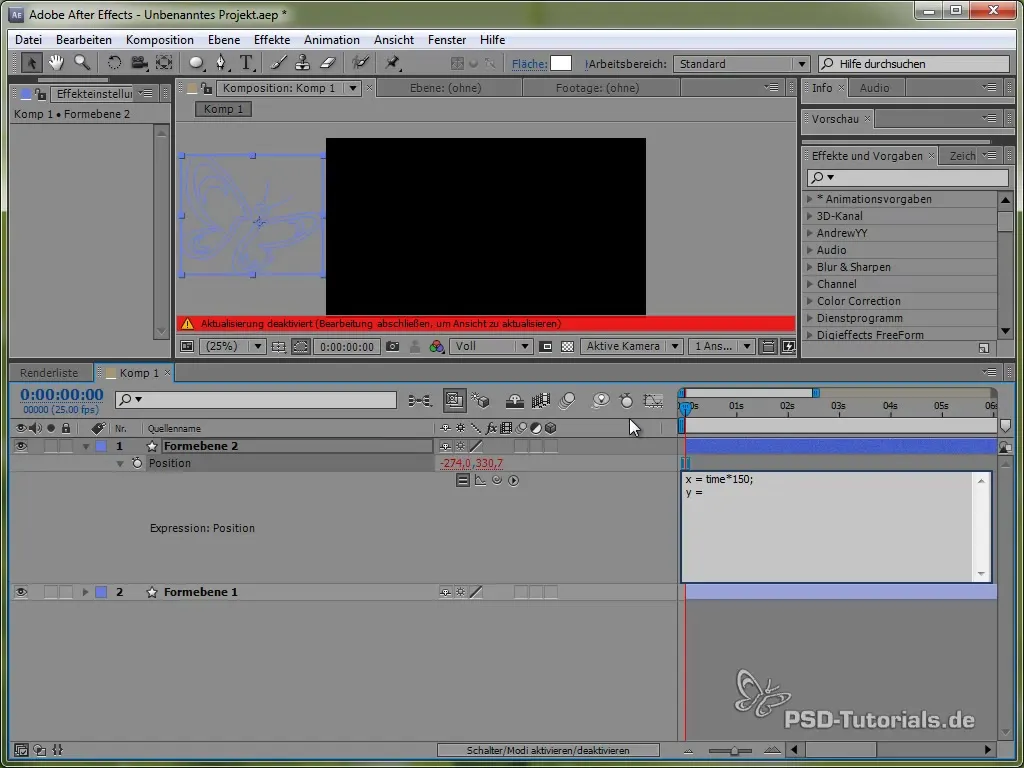
Цей код викликає рух метелика в напрямку X постійно на 150 пікселів за секунду. Для напрямку Y ми будемо використовувати синусоїдальну функцію, яка генерує вертикальний рух метелика та "коливає" його між певними значеннями.
Застосування синусоїдальної функції
Рух Y визначається наступним висловленням:
value[1] + 40 * Math.sin(2 * Math.PI * time)
При цьому Math.sin() реалізує синусоїдальну функцію. Вона варіюється між -1 та 1 і множиться на 40, що означає, що метелик коливається в напрямку Y від -40 до 40 пікселів.
Візуалізація графіку руху
Щоб краще візуалізувати цей рух, ти можеш активувати вікно графіка в After Effects. Це дозволить тобі чіткіше бачити коливання значення синуса.
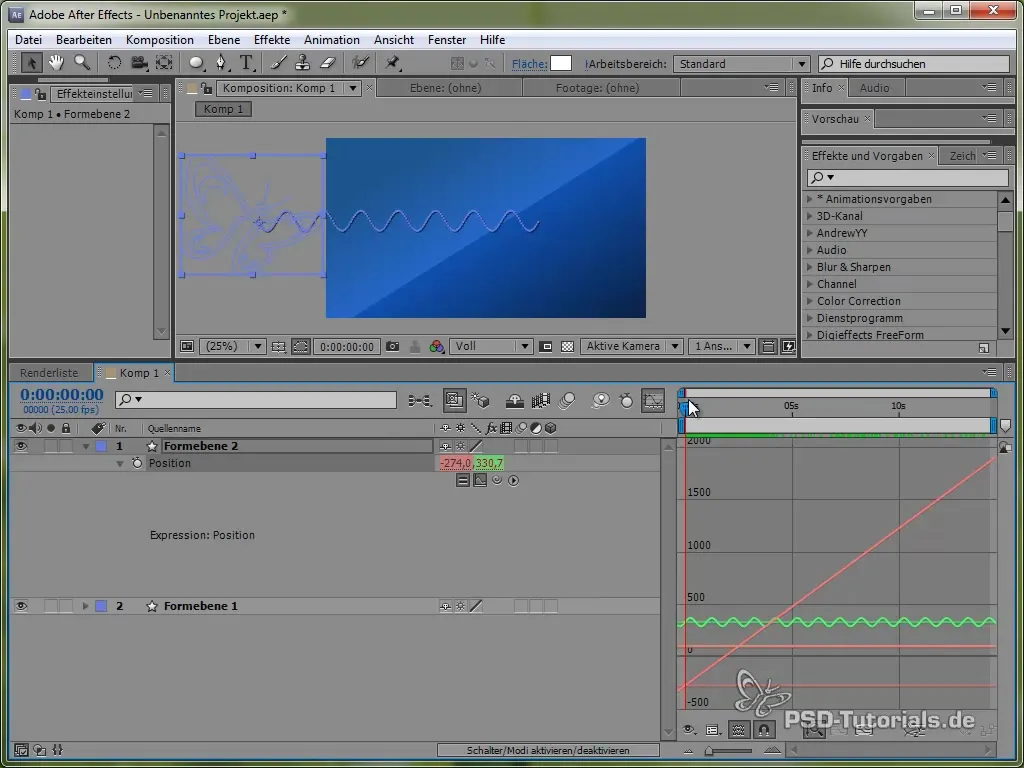
Можна бачити, що сигнал осцилює і рухається по екрану.
Регулювання амплітуди та частоти
Тепер ти можеш відрегулювати амплітуду, щоб створити коливання різної сили. Якщо ти хочеш, наприклад, збільшити амплітуду з часом, можеш використовувати наступне:
40 * (time * 10) * Math.sin(2 * Math.PI * time)
Це викликає збільшення амплітуди з часом, що означає, що метелик коливатиметься на 40 пікселів через одну секунду, на 80 пікселів через дві секунди і так далі.
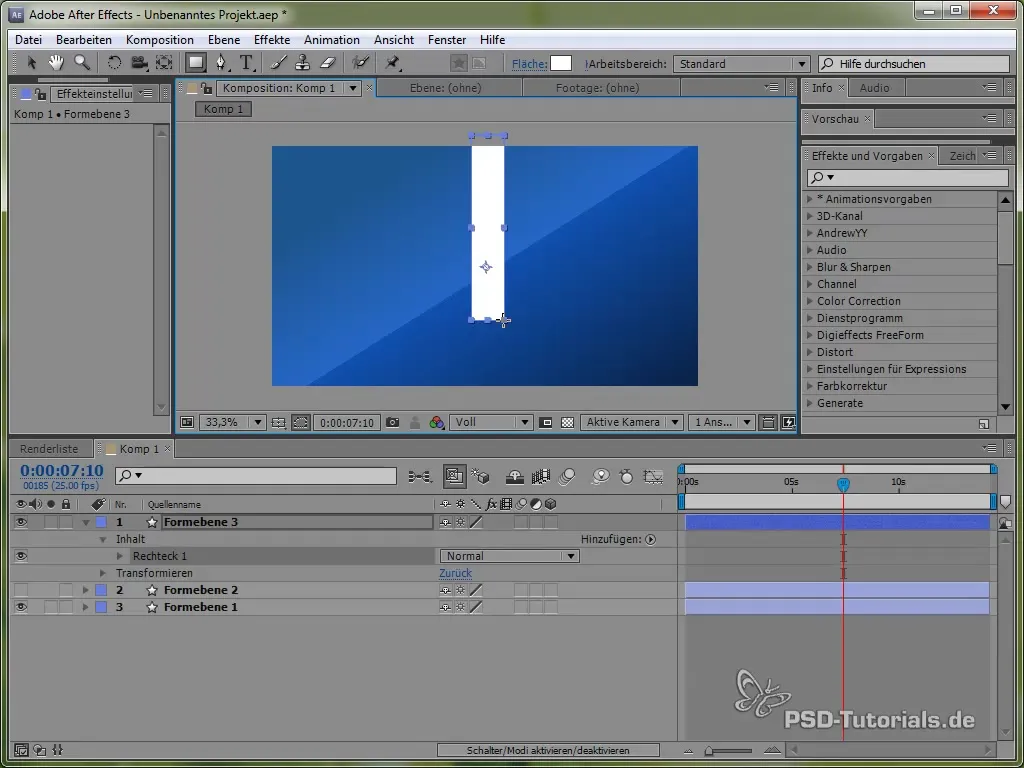
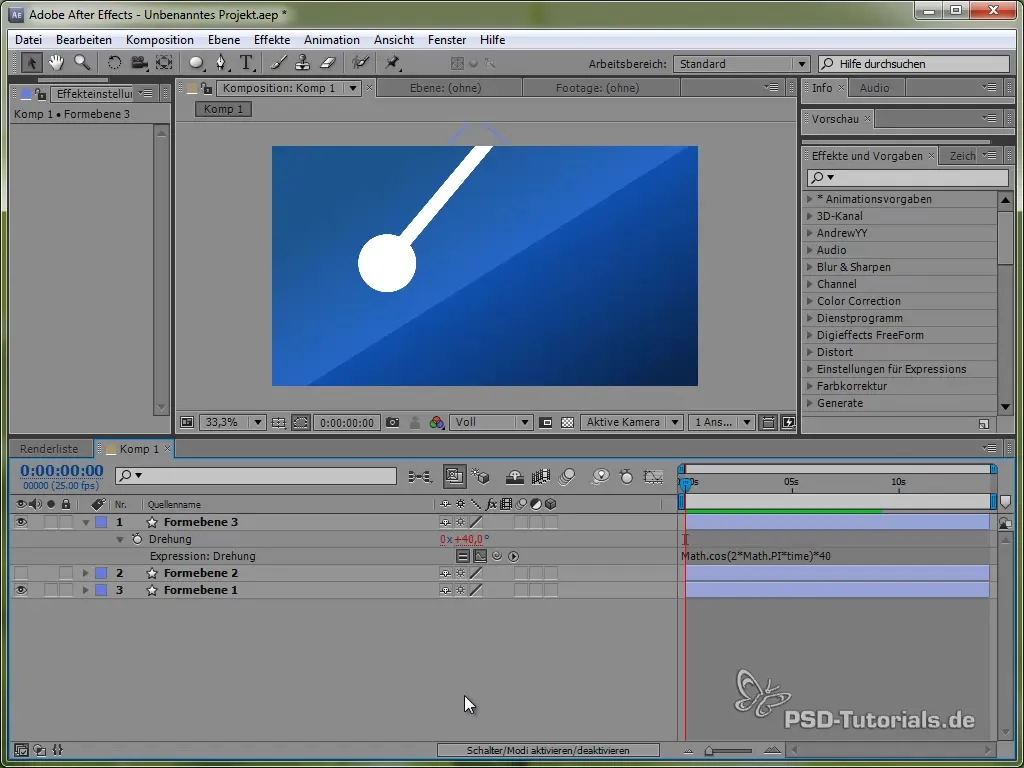
Створення маятника
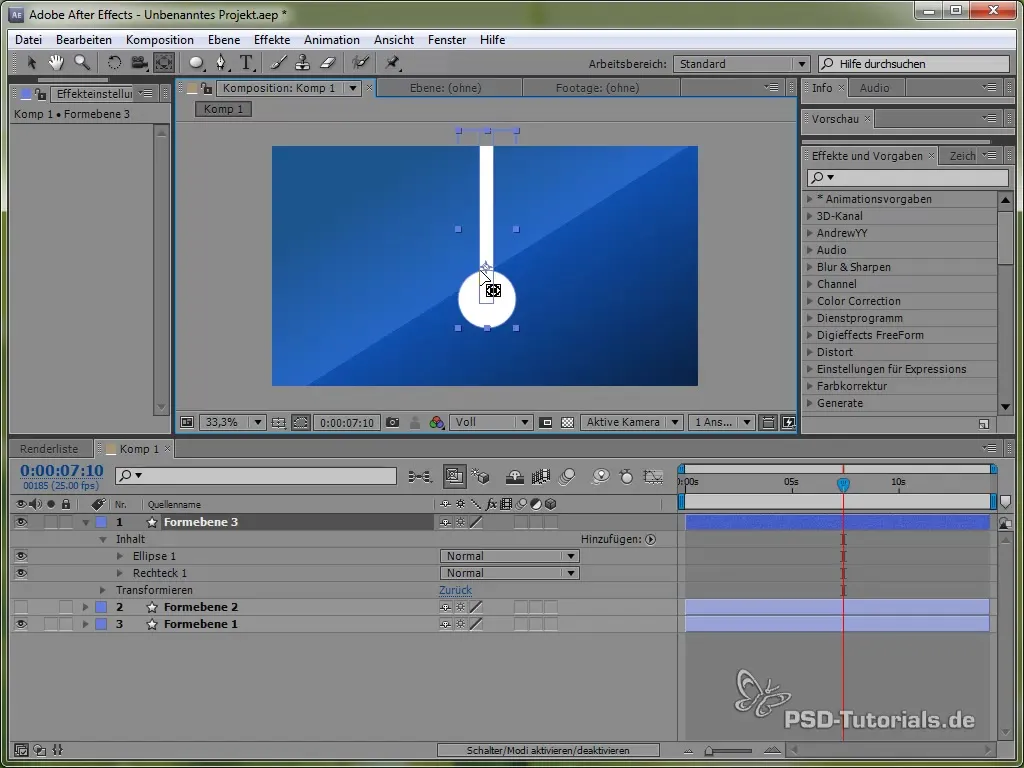
Щоб глибше ознайомитися з різними фізичними симуляціями, ми зараз зосередимося на створенні маятника. Спочатку намалюй тонкий стержень і додай еліпс на його кінці.
Розмісти анкерну точку у верхній частині маятника, щоб він міг коливатися. Це можна зробити за допомогою інструменту для анкерної точки.
Потім встанови висловлення:
value + 40 * Math.cos(2 * Math.PI * time)
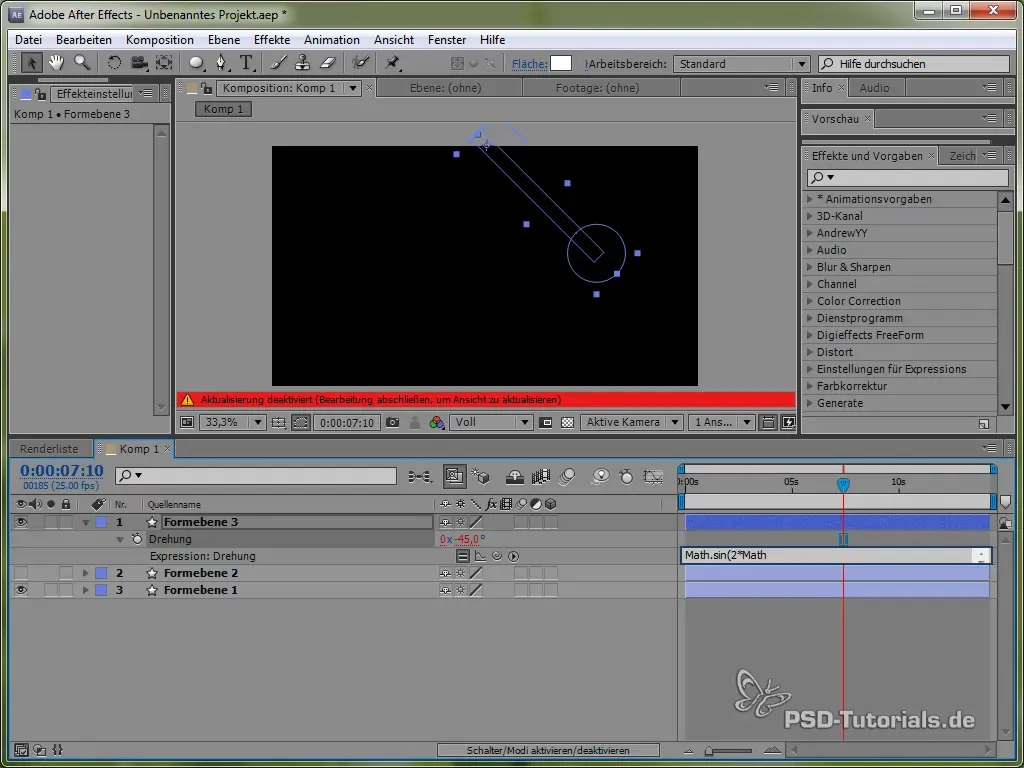
Завдяки косинусу ми починаємо процес коливання з позитивної точки, що є реалістичним, оскільки маятник починає коливатися з верхньої позиції.
Додавання гасіння ефектів
Щоб інтегрувати гасіння в коливання, ми використовуємо експоненціальну функцію. Це робить коливання більш реалістичними, оскільки спочатку вони сильні, а потім поступово зменшуються.
Приклад коду може виглядати так:
40 * Math.cos(2 * Math.PI * time) / Math.exp(time)
Тут ділення через експоненціальну функцію забезпечує повільне гасіння.
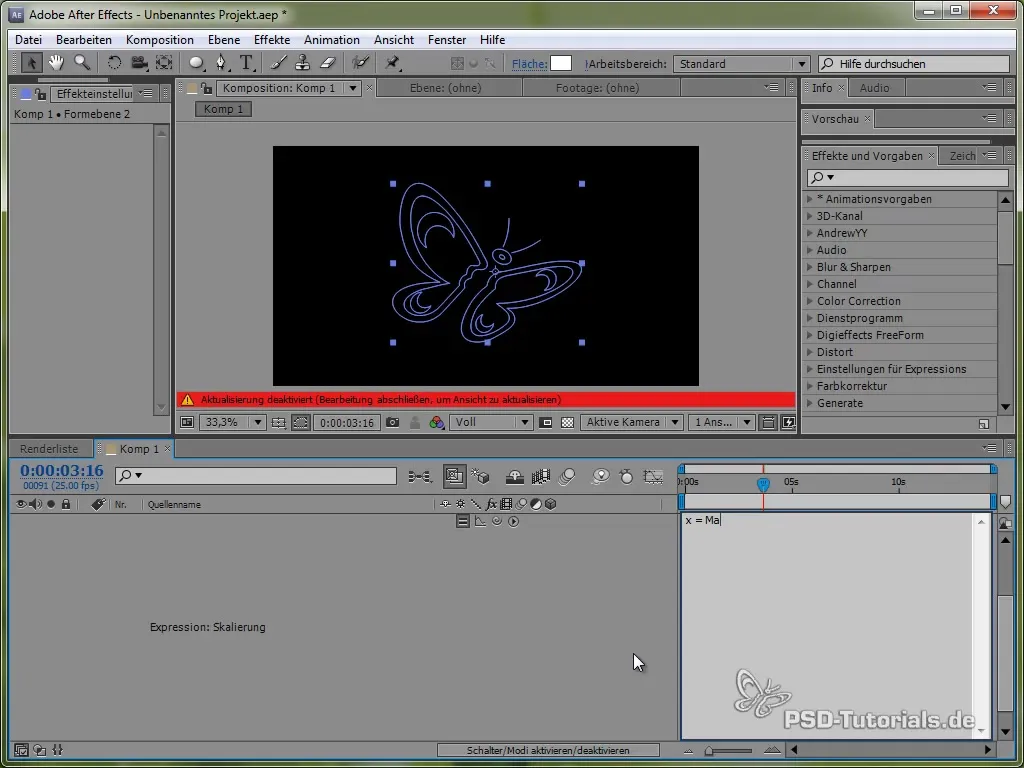
Додавання Squash і Stretch
Для більш живих анімацій ти також можеш додати ефект Squash and Stretch. Це можна зробити через масштабування метелика.
Ти це робиш, застосувавши висловлення до масштабування, яке можна застосувати як до значень x, так і до y, використовуючи синусоідальну або косинусоідальну функцію.
Заключні думки
Можна бачити, що з правильним застосуванням тригонометричних та експоненціальних функцій можна створити дуже реалістичні та цікаві анімації. Ти дізнався, як навести метелика на політ, як змусити маятник коливатися і як працювати з ефектами, такими як Squash і Stretch.
Резюме - Математика в висловленнях: Тригонометричні та експоненціальні функції
Математика в контексті висловлень в After Effects відкриває тобі можливості для створення креативних та яскравих анімацій. Тригонометричні та експоненціальні функції є в цьому суттєвими. У цьому навчальному посібнику ти отримав досвід використання цих математичних концепцій на практиці.
Поширені запитання
Як я можу встановити висловлення в After Effects?Натисни клавішу ALT і клацни на годинник поряд з властивістю, до якої хочеш додати висловлення.
У чому різниця між синусовими та косиновими функціями?Синусова функція починається з 0, тоді як косинусова функція починається з 1. Це впливає на те, як починаються анімації.
Як я можу створити ефекти гасіння?Ти можеш створити ефекти гасіння, вставивши експоненціальні функції у свої висловлення, які зменшують рух з часом.


