Matematikk spiller en fundamental rolle i den digitale verden, og spesielt innen videoredigering med After Effects (AE) gir den deg helt nye muligheter. I denne opplæringen vil du lære hvordan du kan bruke trigonometric og eksponentielle funksjoner i AE som Expressions for å lage fascinerende animasjoner. Et spesielt spennende eksempel vil være bevegelsen til en sommerfugl, som viser deg hvordan fysiske simuleringer kan implementeres ved hjelp av matematikk.
Viktigste funn
- Trigonometriske funksjoner som sinus og cosinus kan brukes til å lage forskjøvede bevegelser.
- Eksponentielle funksjoner brukes til å simulere dempingseffekter.
- Bruken av absoluttverdier i funksjoner kan hjelpe med å oppnå spesifikke animasjonseffekter.
Trinn-for-trinn veiledning
Setter sommerfuglen i bevegelse
For å sette sommerfuglen i bevegelse må du først animere den slik at den beveger seg i bølger. Denne bølgebevegelsen kan enkelt realiseres med hjelpe av Expressions.
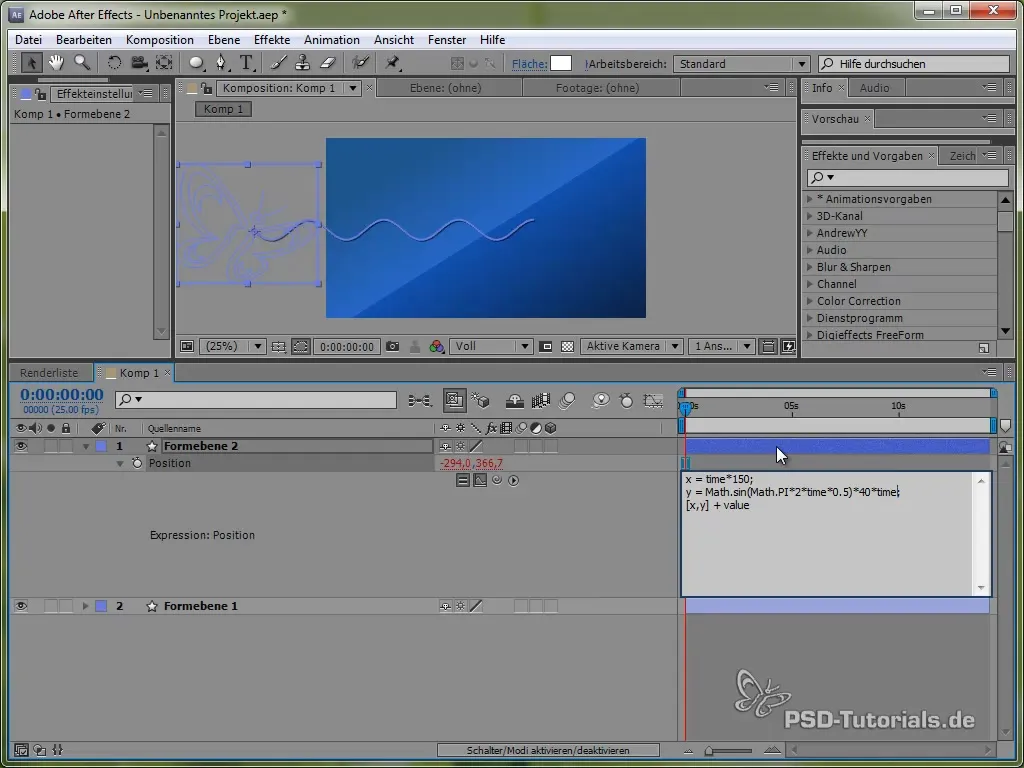
Begynn med å åpne posisjonen til sommerfuglen ved å trykke på tasten "P". Deretter setter du en Expression for posisjonen ved å holde ALT-tasten inne og klikke på klokken.
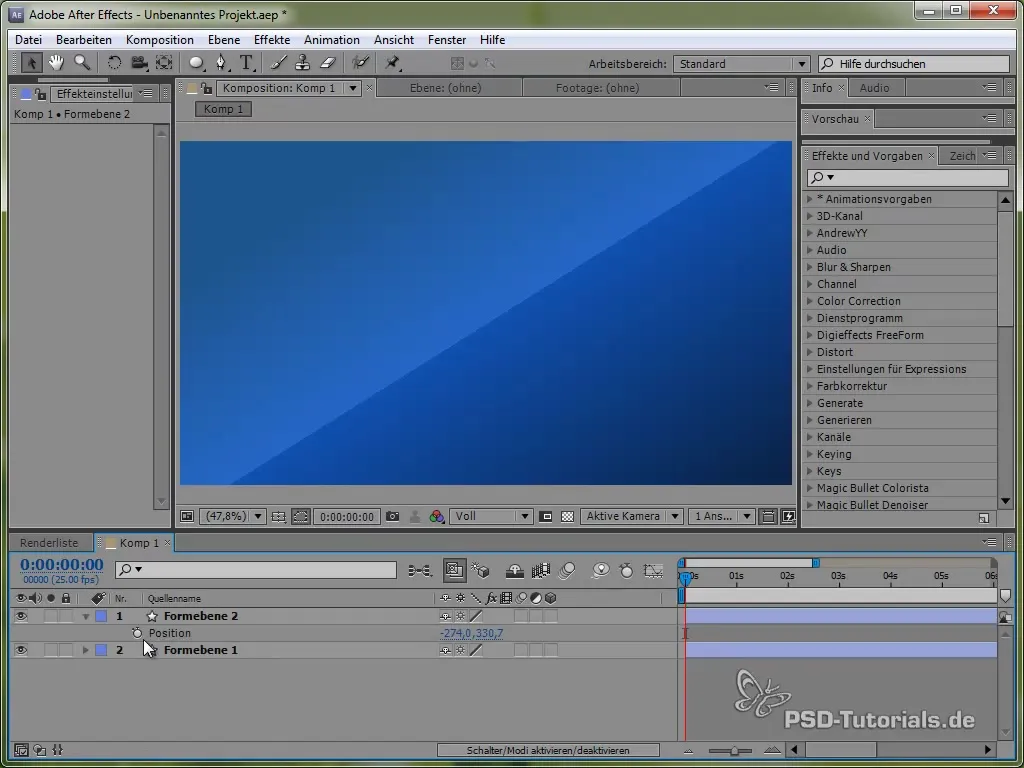
Til dette bruker vi først tidsvariabelen time, multiplisert med en verdi som bestemmer hastigheten på bevegelsen. For eksempel:
value[0] + time * 150
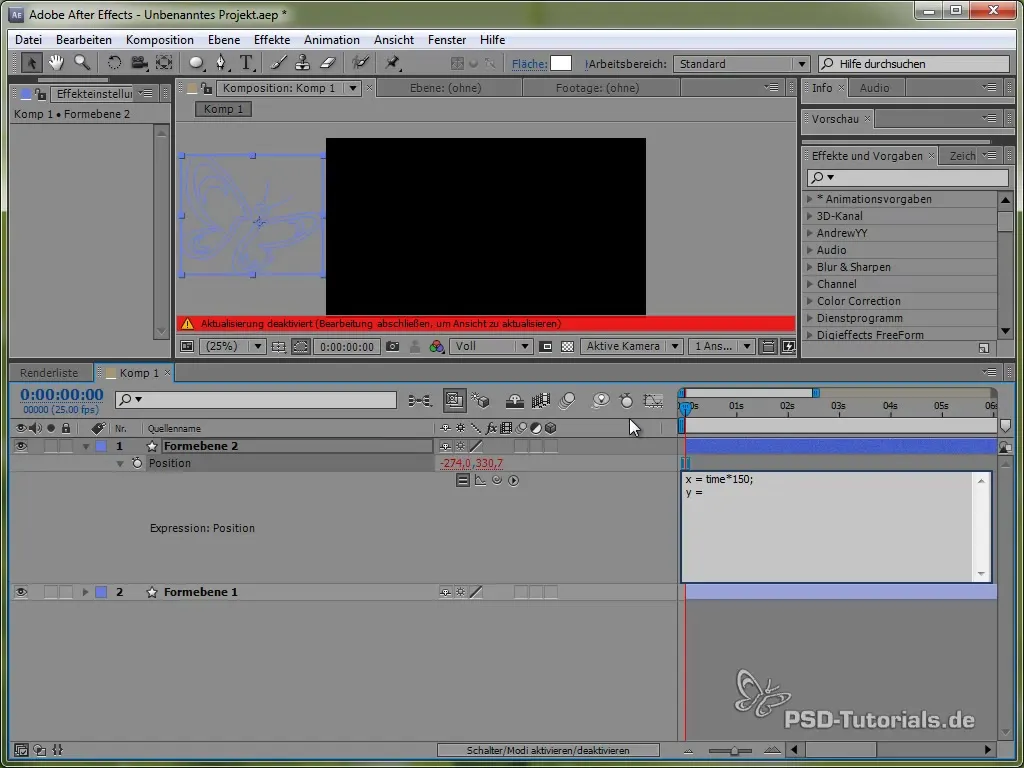
Denne koden får sommerfuglen til å bevege seg konstant 150 piksler per sekund i X-retningen. For Y-retningen vil vi bruke en sinusfunksjon som skaper den vertikale bevegelsen til sommerfuglen og får den til å "vake" mellom bestemte verdier.
Bruk av sinusfunksjonen
Y-bevegelsen defineres av følgende Expression:
value[1] + 40 * Math.sin(2 * Math.PI * time)
Her implementerer Math.sin() sinusfunksjonen. Den varierer mellom -1 og 1 og multipliseres med 40, noe som betyr at sommerfuglen "vaker" mellom -40 og 40 piksler i Y-retningen.
Visualisere bevegelsens grafikk
For å visualisere denne bevegelsen bedre kan du aktivere grafvinduet i After Effects. Dette vil vise deg svingningene av sinusverdien tydeligere.
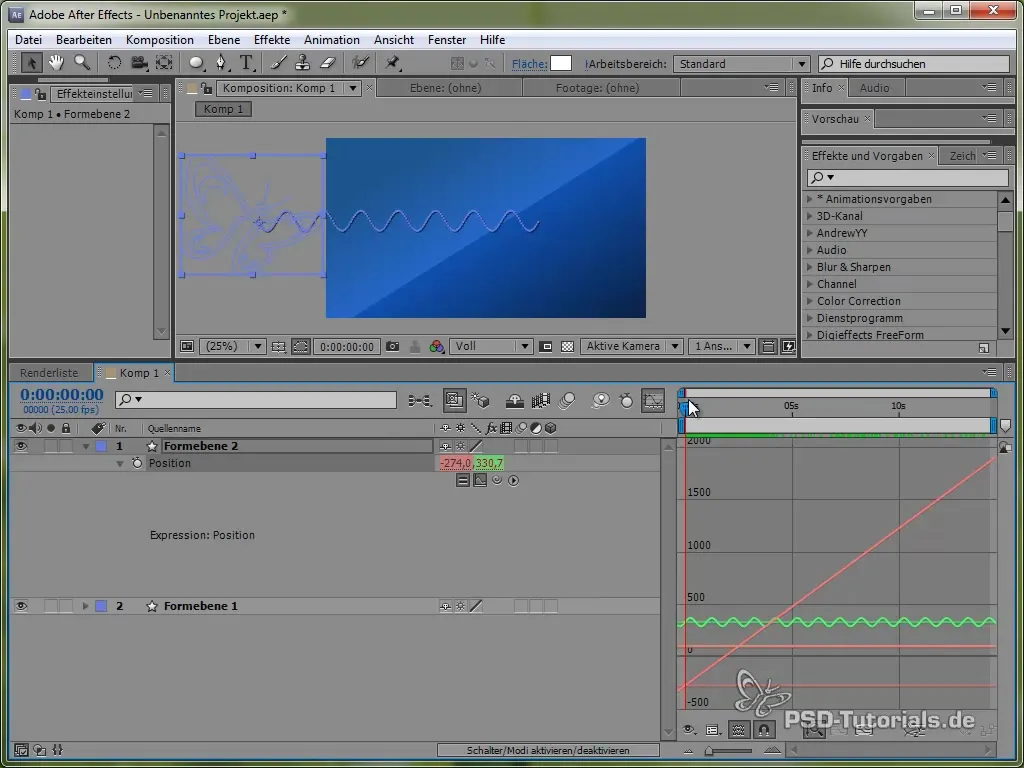
Man ser at signalet oscillerer og beveger seg over skjermen.
Variere amplitude og frekvens
Nå kan du justere amplituden for å skape ulike nivåer av svingninger. Hvis du for eksempel ønsker å øke amplituden over tid, kan du bruke følgende:
40 * (time * 10) * Math.sin(2 * Math.PI * time)
Dette vil gjøre at amplituden øker over tid, hvilket vil få sommerfuglen til å svinge 40 piksler etter ett sekund, 80 piksler etter to sekunder, og så videre.
Opprette en pendel
For å dykke dypere inn i håndteringen av forskjellige fysiske simuleringer, går vi nå over til opprettelsen av en pendel. Tegn først en tynn stang og legg til en ellipse på enden.
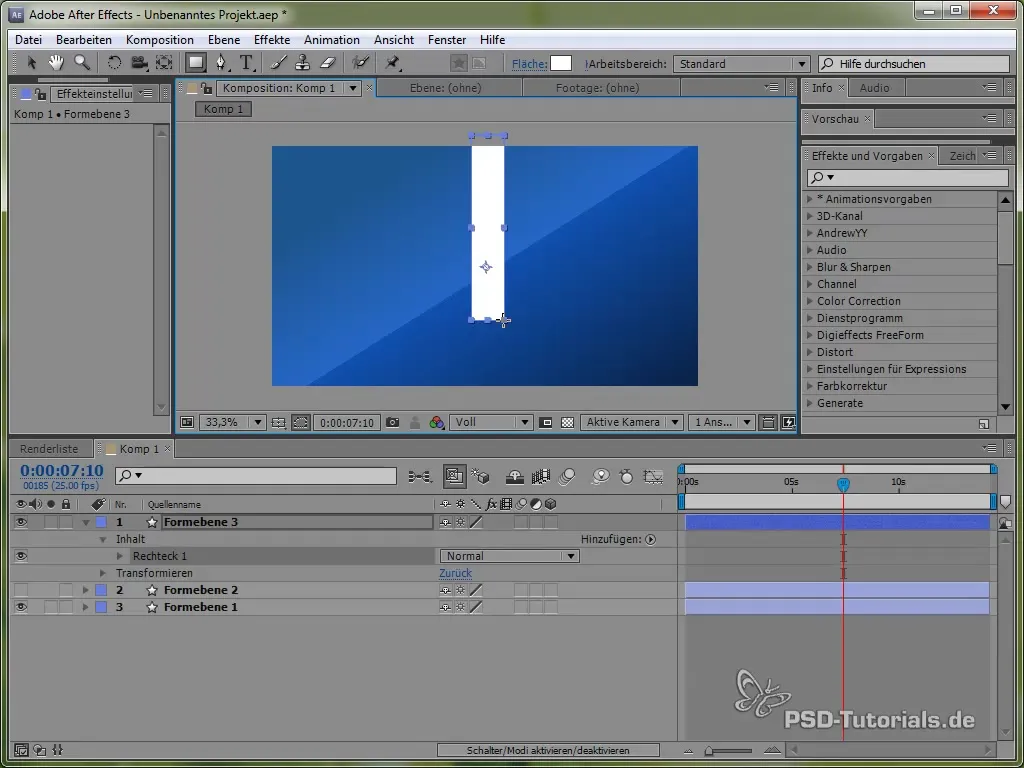
Plasser ankerpunktet øverst på pendelen, slik at den kan svinge. Dette gjøres med verktøyet for ankerpuntet.
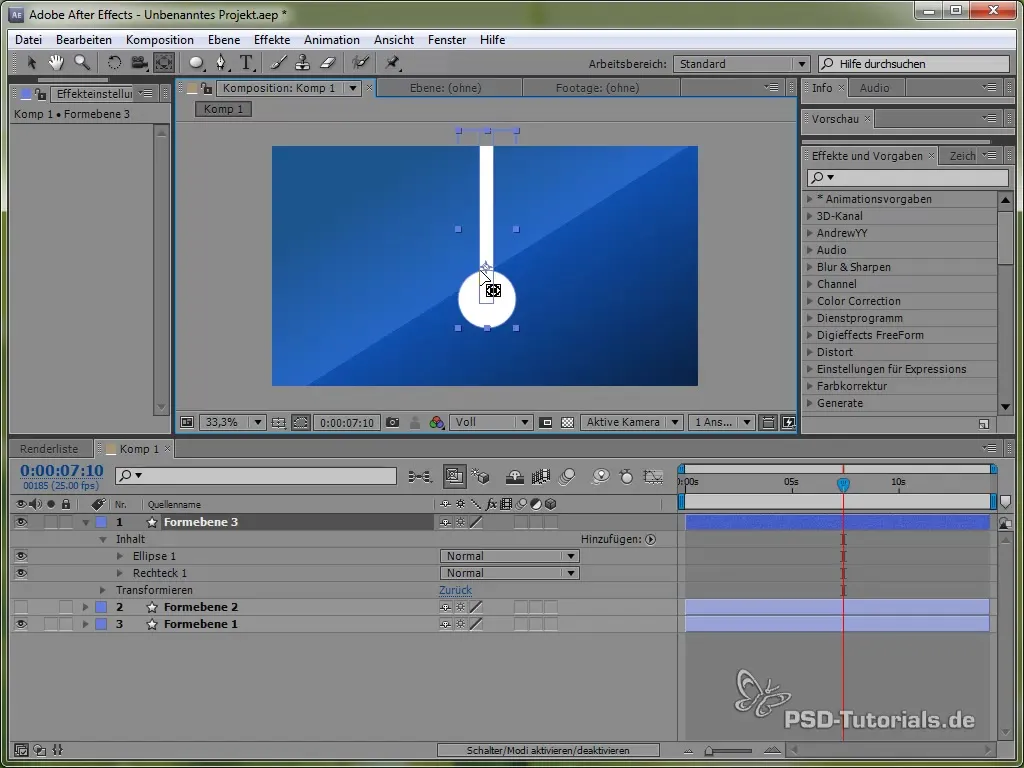
Sett deretter Expression:
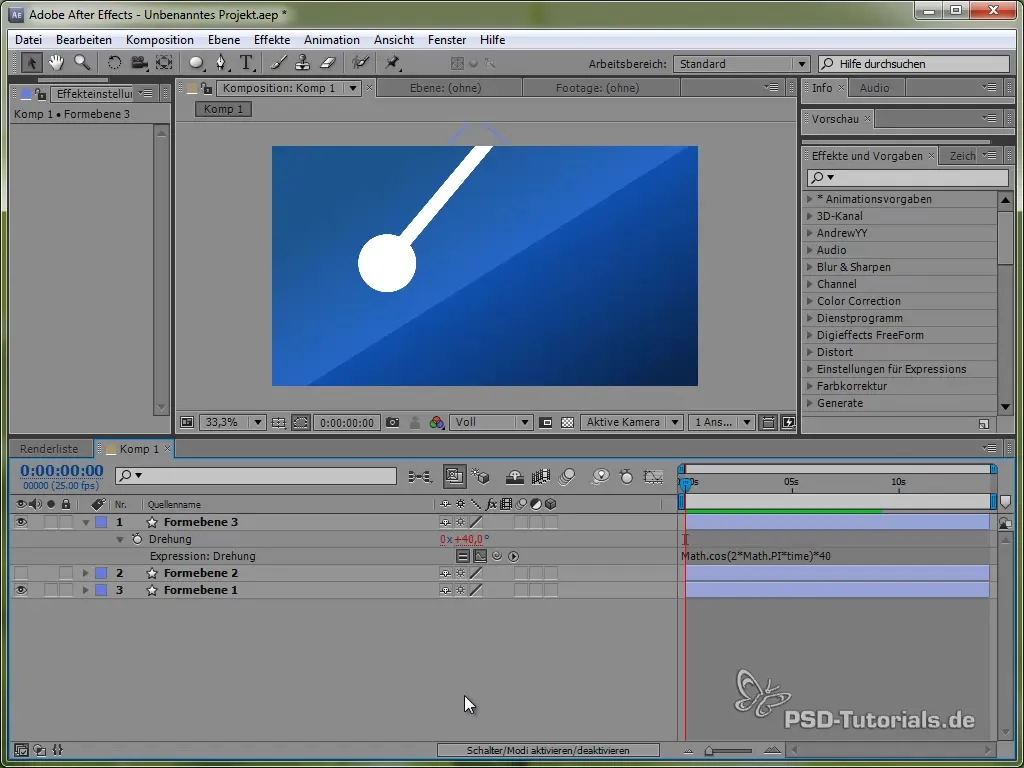
value + 40 * Math.cos(2 * Math.PI * time)
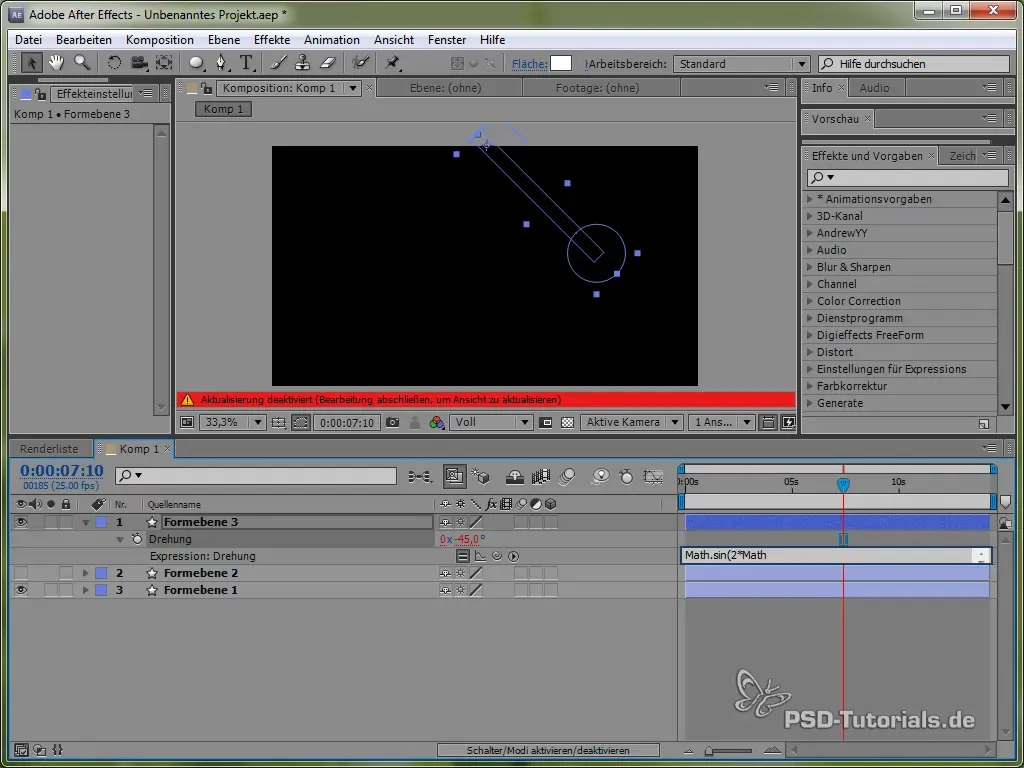
Ved å bruke cosinus starter vi svingningsprosessen fra et positivt punkt, noe som er realistisk, siden pendelen begynner å svinge fra toppen.
Legge til dempingseffekter
For å integrere demping i svingningen, bruker vi den eksponentielle funksjonen. Dette gjør at svingningen virker mer realistisk, da den er sterk i begynnelsen og til slutt avtar.
En eksempel-kode kan se slik ut:
40 * Math.cos(2 * Math.PI * time) / Math.exp(time)
Her sørger divisjonen gjennom eksponentialfunksjonen for en langsom demping.
Legge til squash og stretch
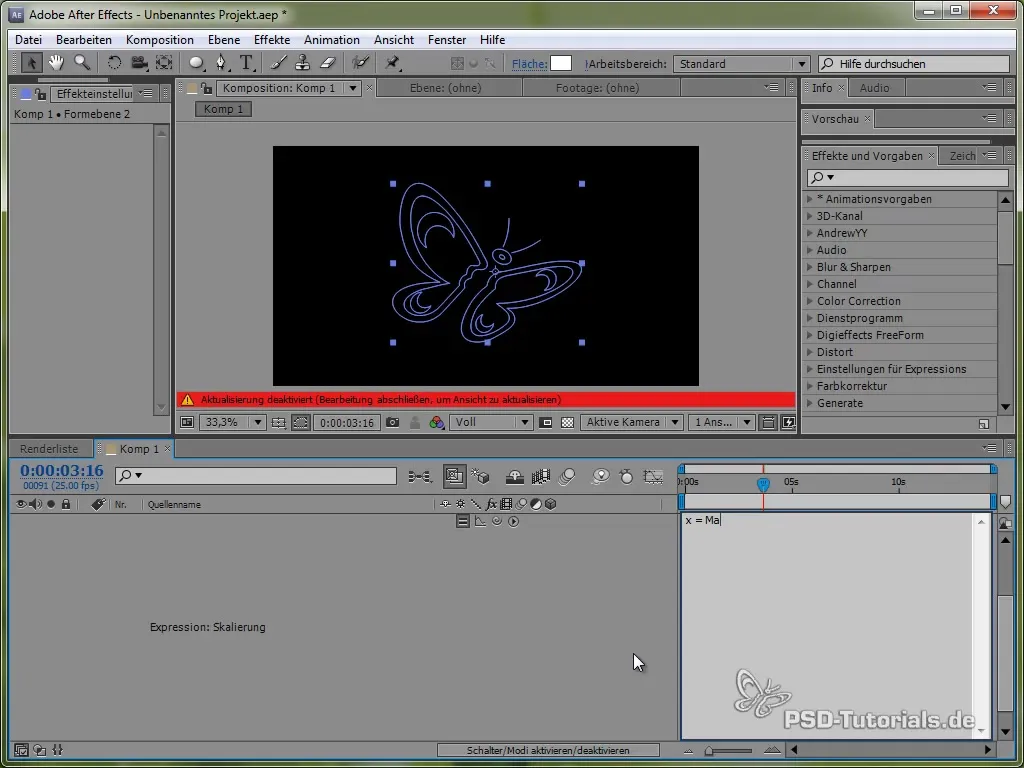
For mer livlige animasjoner kan du også legge til squash- og stretch-effekten. Dette kan du oppnå ved å skalere sommerfuglen.
Du gjør dette ved å bruke en Expression på skaleringsverdien, som kan brukes både på x- og y-verdier, ved å bruke en sinus- eller cosinusfunksjon.
Avsluttende tanker
Det er tydelig at ved riktig bruk av trigonometriske og eksponentielle funksjoner kan man skape svært realistiske og interessante animasjoner. Du har lært hvordan man lar en sommerfugl fly, hvordan man får en pendel til å svinge, og hvordan man arbeider med effekter som squash og stretch.
Sammendrag - Matematikk i Expressions: Trigonometriske & Eksponentielle funksjoner
Matematikk i konteksten av Expressions i After Effects gir deg muligheten til å lage kreative og livlige animasjoner. Trigonometriske og eksponentielle funksjoner er essensielle i denne prosessen. I denne opplæringen har du fått erfaring med å bruke disse matematiske konseptene i praksis.
Ofte stilte spørsmål
Hvordan setter jeg en Expression i After Effects?Hold ALT-tasten inne og klikk på klokken ved siden av egenskapen du ønsker å legge til en Expression for.
Hva er forskjellen mellom sinus- og cosinusfunksjoner?Sinusfunksjonen starter ved 0, mens cosinusfunksjonen starter ved 1. Dette har påvirkning på hvordan animasjoner starter.
Hvordan kan jeg lage dempingseffekter?Du kan lage dempingseffekter ved å inkludere eksponentielle funksjoner i dine Expressions som reduserer bevegelsen over tid.


