Die Möglichkeit, mit Python mathematische Konzepte wie den größten gemeinsamen Nenner (ggT) zu implementieren, ist eine wertvolle Fähigkeit für jeden Programmierer. In dieser Anleitung wirst du lernen, wie du mithilfe von While-Schleifen ein Programm schreibst, das den ggT aus zwei Zahlen berechnet. Du wirst Schritt für Schritt durch den Prozess geführt, sodass du am Ende selbstständig ein funktionierendes Programm erstellen kannst.
Wichtigste Erkenntnisse
- Der größte gemeinsame Nenner (ggT) kann durch wiederholtes Anwenden des Modulo-Operators ermittelt werden.
- While-Schleifen sind ein effektives Mittel, um wiederholte Berechnungen durchzuführen, solange eine bestimmte Bedingung erfüllt ist.
Schritt-für-Schritt-Anleitung
Schritt 1: Vorbereitung der Variablen
Zuerst legst du zwei Zahlen als Variablen fest, mit denen du arbeiten möchtest. Diese Werte werden in den folgenden Berechnungen verwendet.
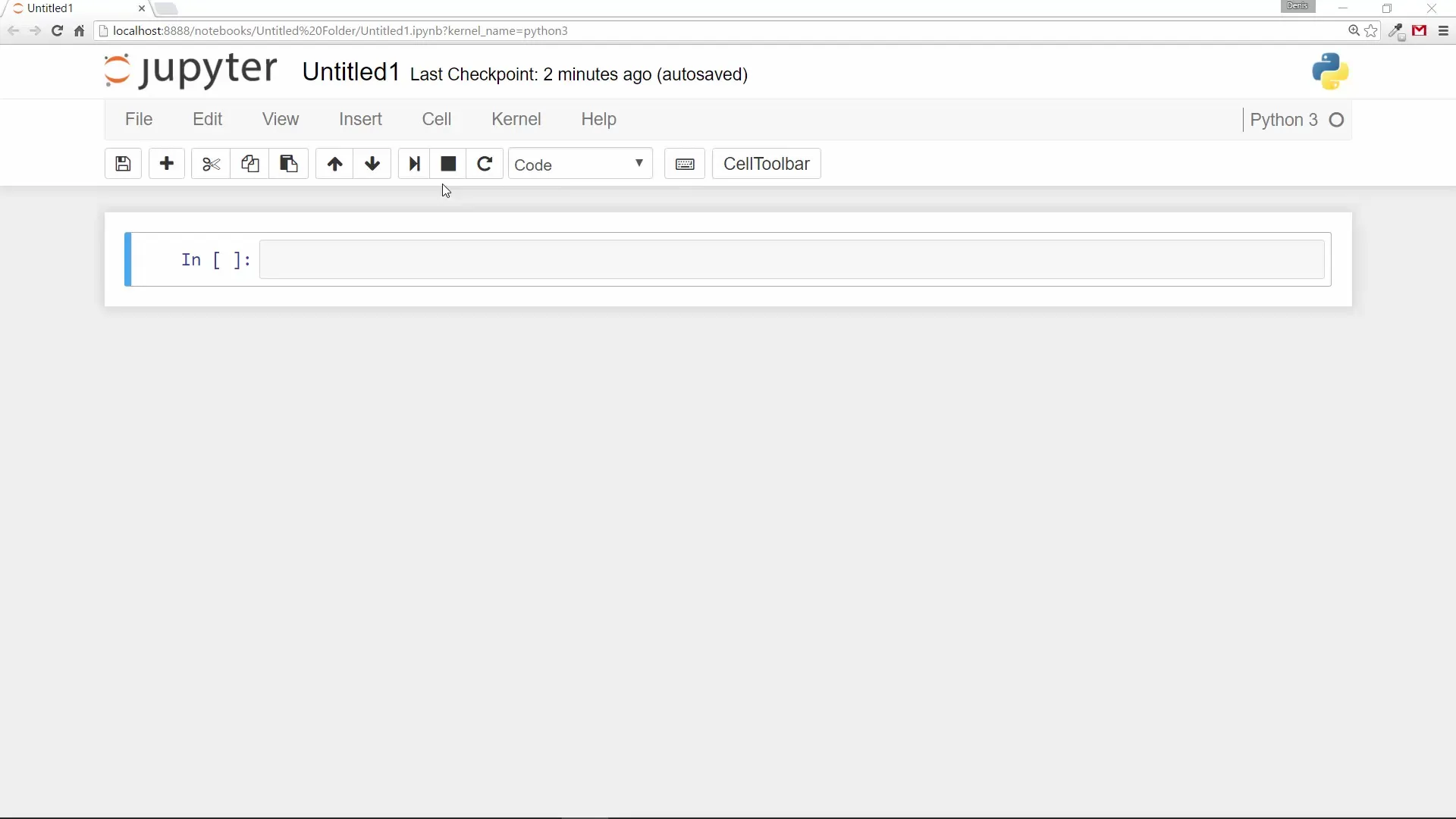
Schritt 2: Initialisierung des ggT
Du gibst der ggn-Variablen initial den Wert der zweiten Zahl. Dies ist der Ausgangspunkt für die Berechnung.
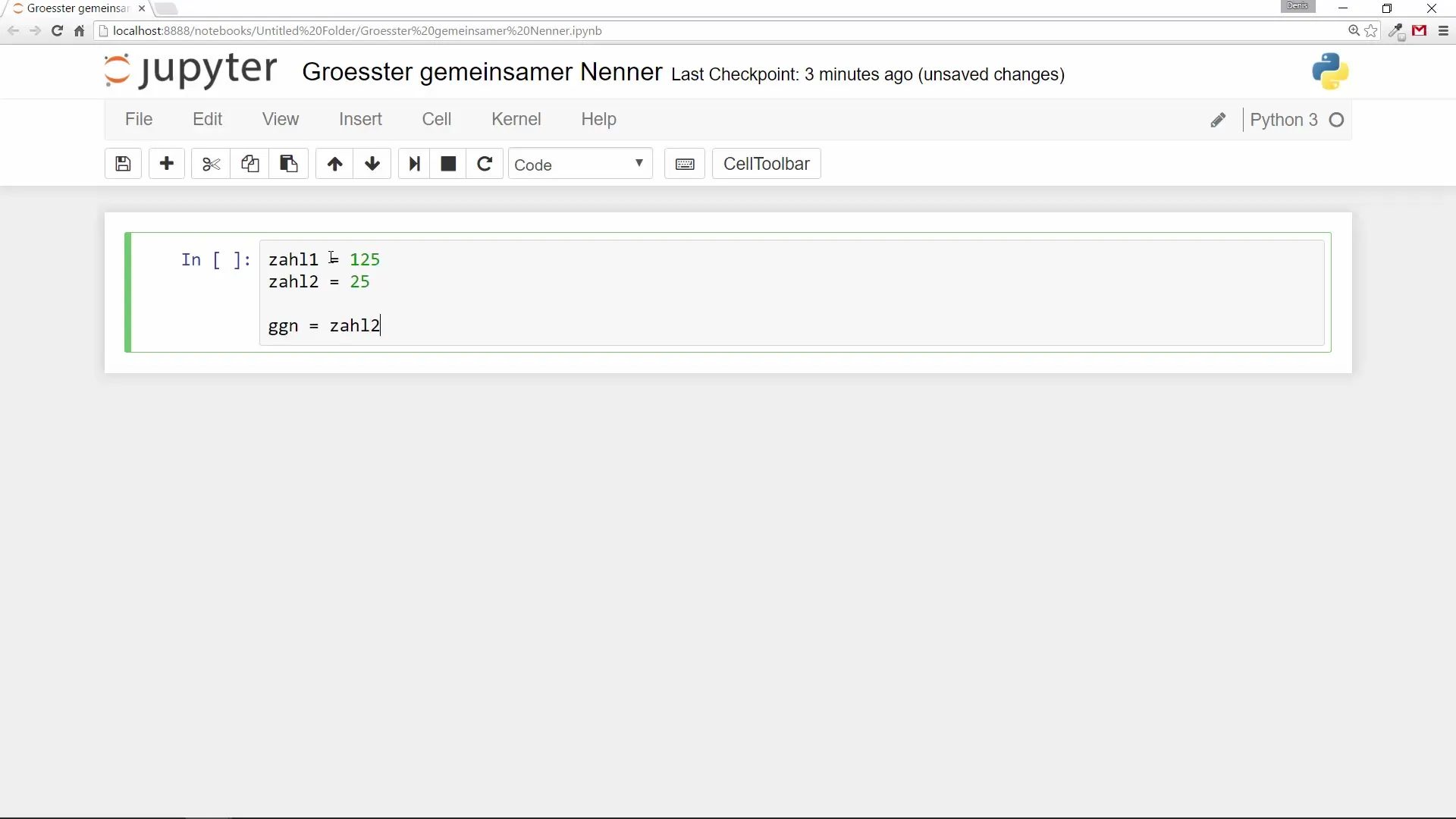
Schritt 3: Erstellen der While-Schleife
Nun erstellst du eine While-Schleife, die so lange läuft, wie die erste Zahl größer als Null ist. Innerhalb dieser Schleife geschieht die Hauptlogik der Berechnung des ggT.
Schritt 4: Anwendung des Modulo-Operators
Innerhalb der Schleife ersetzt du den Wert der ersten Zahl durch den aktuellen Wert der zweiten Zahl und die zweite Zahl durch den Rest der ersten Zahl geteilt durch die zweite Zahl (Modulo-Berechnung).
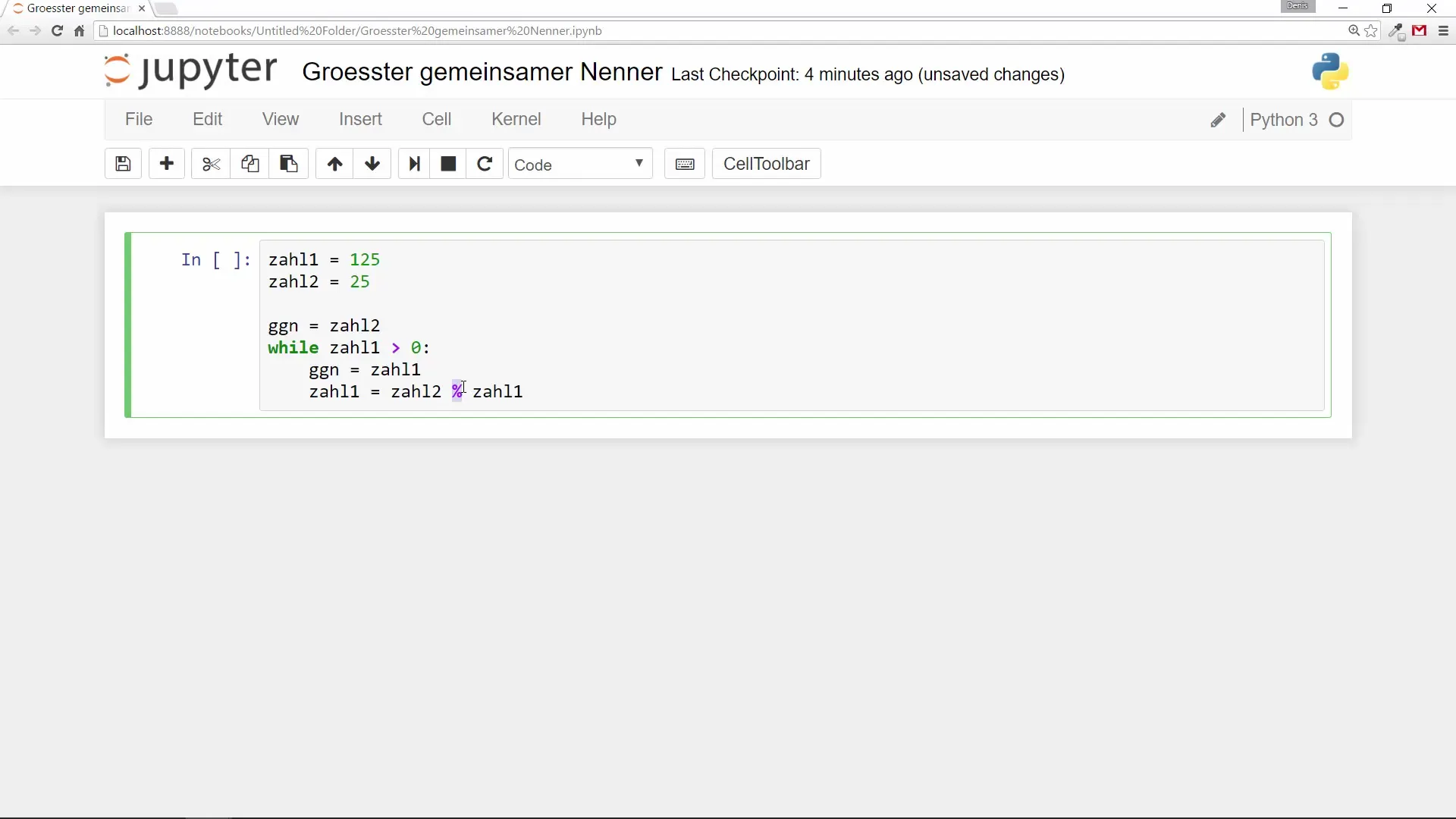
Schritt 5: Ausgabe der Zwischenstände
Es ist sinnvoll, die Werte beider Zahlen in jedem Schleifendurchlauf auszugeben. So kannst du nachvollziehen, wie sich die Werte verändern.
Schritt 6: Berechnung des Ergebnisses
Wenn die Schleife endet, gibst du das Ergebnis mit einem Print-Befehl aus, der dir zeigt, welcher der größte gemeinsame Nenner ist. Hierbei wird die ggn-Variable verwendet, die den Wert des größten gemeinsamen Nenners speichert.
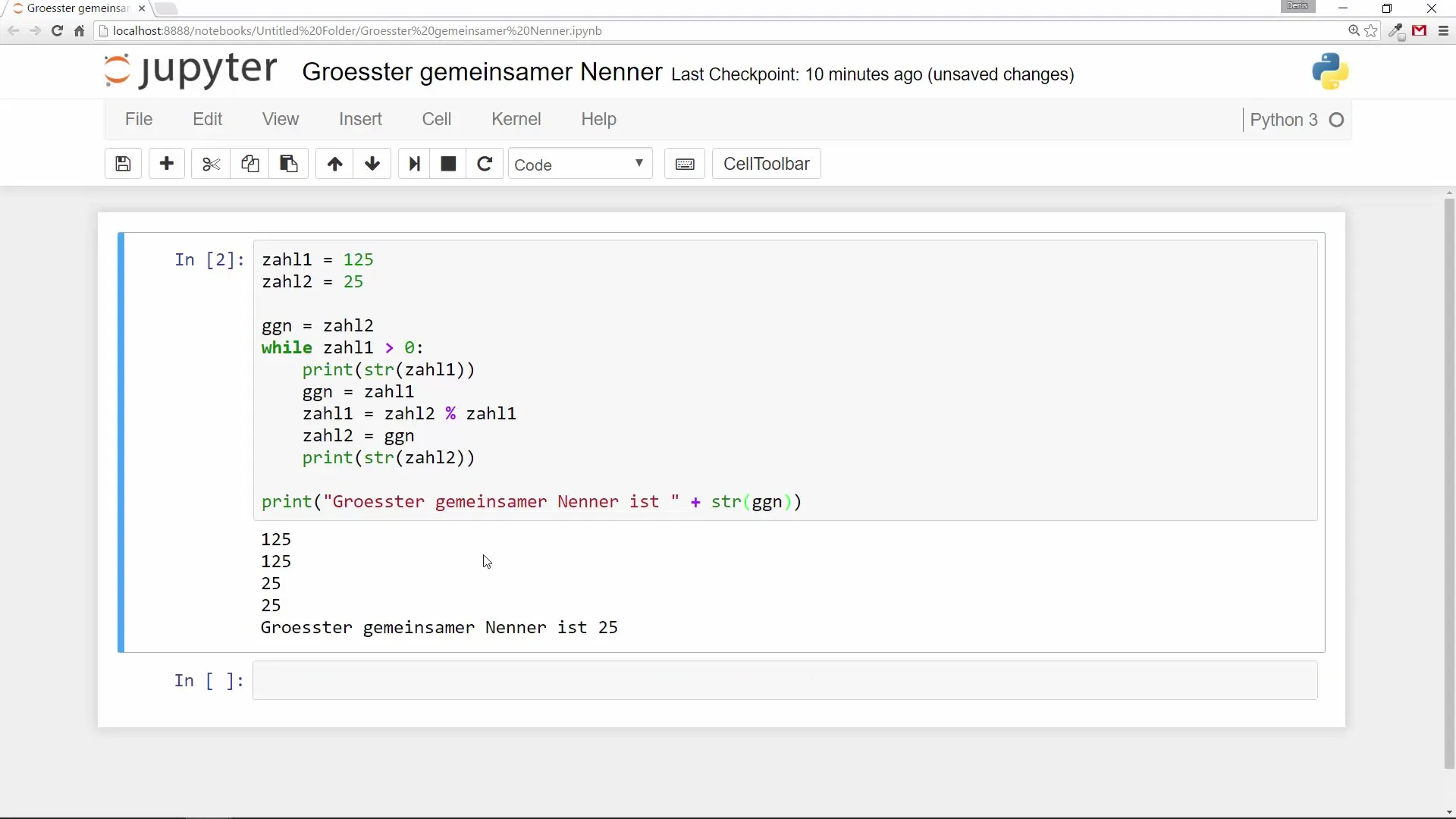
Schritt 7: Test mit unterschiedlichen Werten
Teste dein Programm mit verschiedenen Zahlen, um sicherzustellen, dass es korrekt funktioniert. Du kannst mit kleineren Zahlen beginnen und dann zu größeren und komplexeren Zahlen übergehen. Überprüfe die Ausgaben für deine unterschiedlichen Testfälle.
Schritt 8: Analyse des Programms
Warum funktioniert das Programm? Die logische Struktur, die du entwickelt hast, ist darauf ausgelegt, nacheinander kleinere Zahlen zu finden, die die Bedingungen für den größten gemeinsamen Nenner erfüllen, bis diese exakte Zahl gefunden wird.
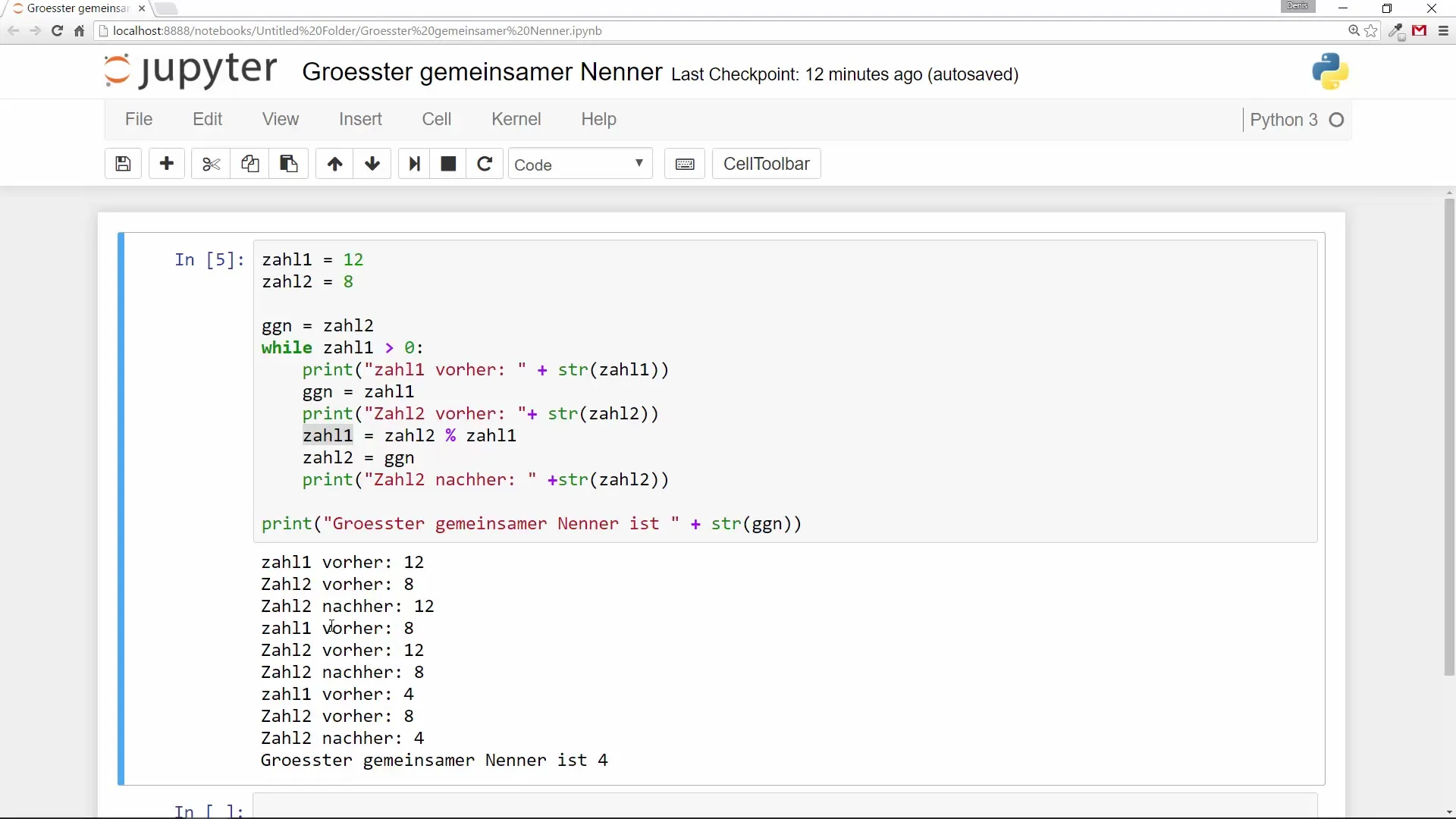
Zusammenfassung – Größter gemeinsamer Nenner mit Python: Eine Schritt-für-Schritt-Anleitung
In dieser Anleitung hast du gelernt, wie du mit Python und einer While-Schleife den größten gemeinsamen Nenner aus zwei Zahlen berechnest. Die Verwendung des Modulo-Operators ermöglicht es dir, den ggT schrittweise zu ermitteln, während du durch die Schleife iterierst.
Häufig gestellte Fragen
Was ist der größte gemeinsame Nenner?Der größte gemeinsame Nenner (ggT) ist die größte Zahl, die beide Zahlen ohne Rest teilen kann.
Wie funktioniert der Modulo-Operator?Der Modulo-Operator gibt den Rest einer Division zurück.
Was ist eine While-Schleife?Eine While-Schleife führt einen Block von Code so lange aus, wie eine bestimmte Bedingung erfüllt ist.
Wie kann ich mein Programm testen?Ändere die Werte der beiden Zahlen und rufe das Programm erneut auf, um den ggT für unterschiedliche Eingaben zu ermitteln.
Könnte ich das Programm auch für mehr als zwei Zahlen verwenden?Technisch, ja, aber es müsste eine andere Logik implementiert werden, um mehrere Zahlen zu berücksichtigen.


