Mathe in Expressions: Trigonometrische & Exponentielle Konzepte

Mathematik spielt in der digitalen Welt eine fundamentale Rolle und vor allem in der Videobearbeitung mit After Effects (AE) eröffnet sie dir gänzlich neue Möglichkeiten. In diesem Tutorial wirst du lernen, wie du trigonometrische und exponentielle Funktionen in AE als Expressions nutzen kannst, um faszinierende Animationen zu erstellen. Ein besonders spannendes Beispiel wird die Bewegung eines Schmetterlings sein, die dir zeigt, wie physikalische Simulationen mithilfe von Mathematik umgesetzt werden können.

Wichtigste Erkenntnisse

• Trigonometrische Funktionen wie Sinus und Cosinus können verwendet werden, um versetzte Bewegungen zu erzeugen.
• Exponentielle Funktionen werden verwendet, um Dämpfungseffekte zu simulieren.
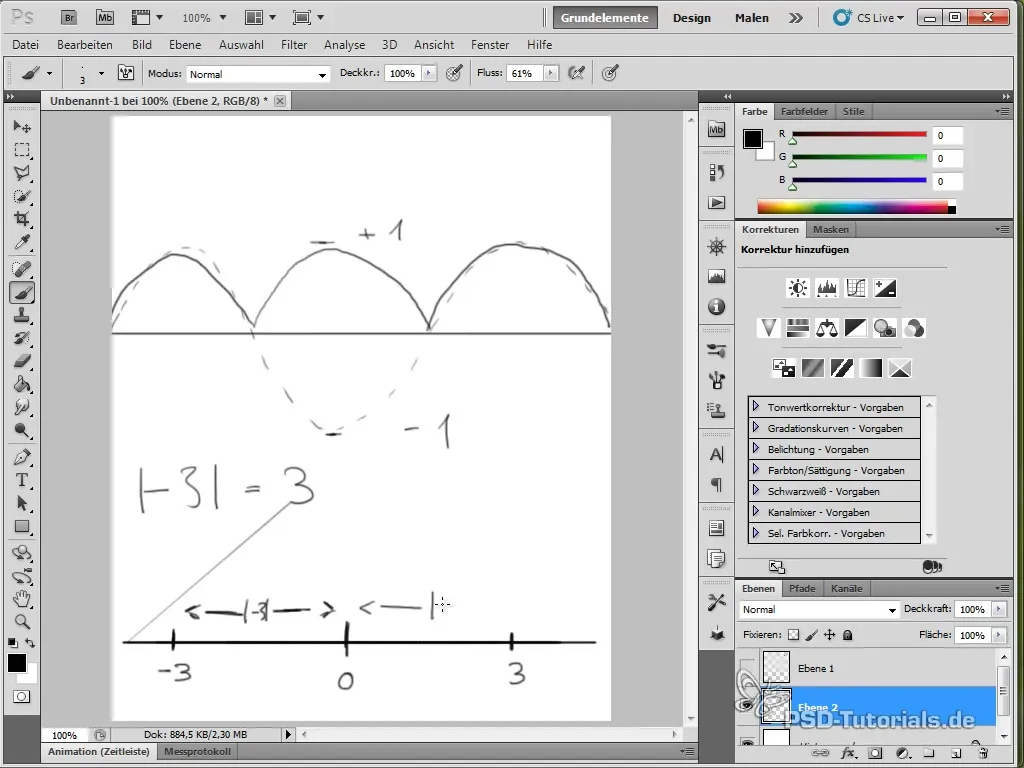
• Die Verwendung von Absolutwerten in Funktionen kann helfen, bestimmte Animationseffekte zu erzielen.

Schritt-für-Schritt-Anleitung

Schmetterling in Bewegung versetzen

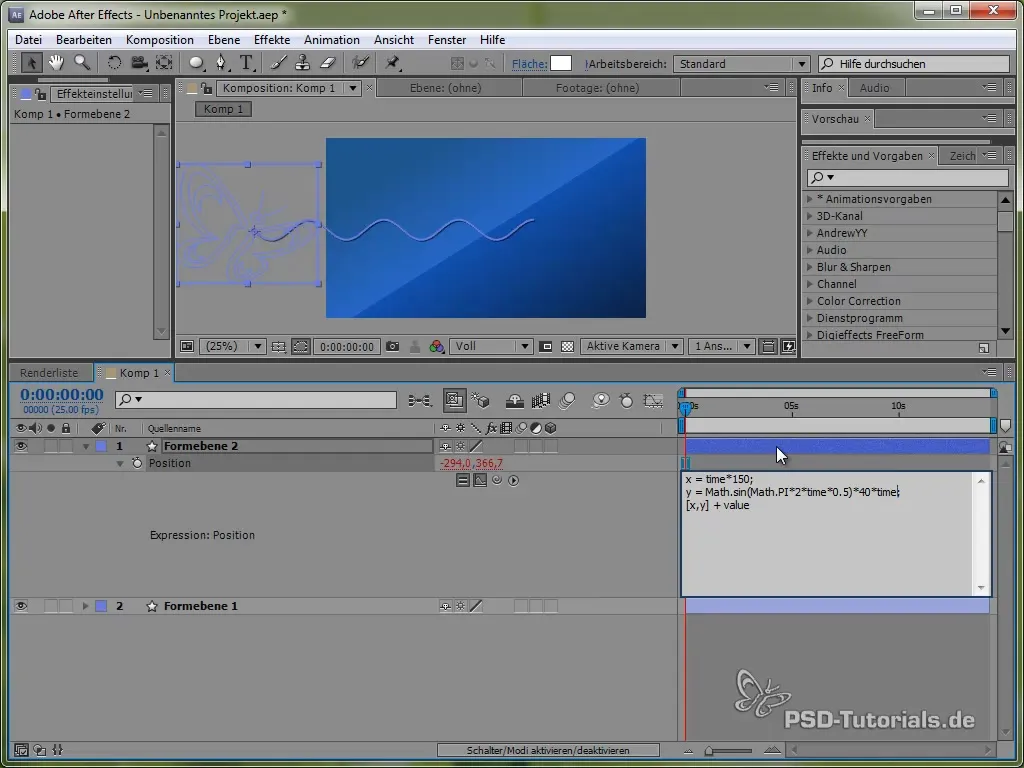
Um unseren Schmetterling in Bewegung zu versetzen, musst du ihn erst einmal derart animieren, dass er sich in einer Welle bewegt. Diese Wellenbewegung lässt sich ohne großen Aufwand über Expressions realisieren.

Beginne, indem du die Position des Schmetterlings durch Drücken der Taste „P“ öffnest. Setze dann eine Expression für die Position, indem du die ALT-Taste drückst und auf die Uhr klickst.

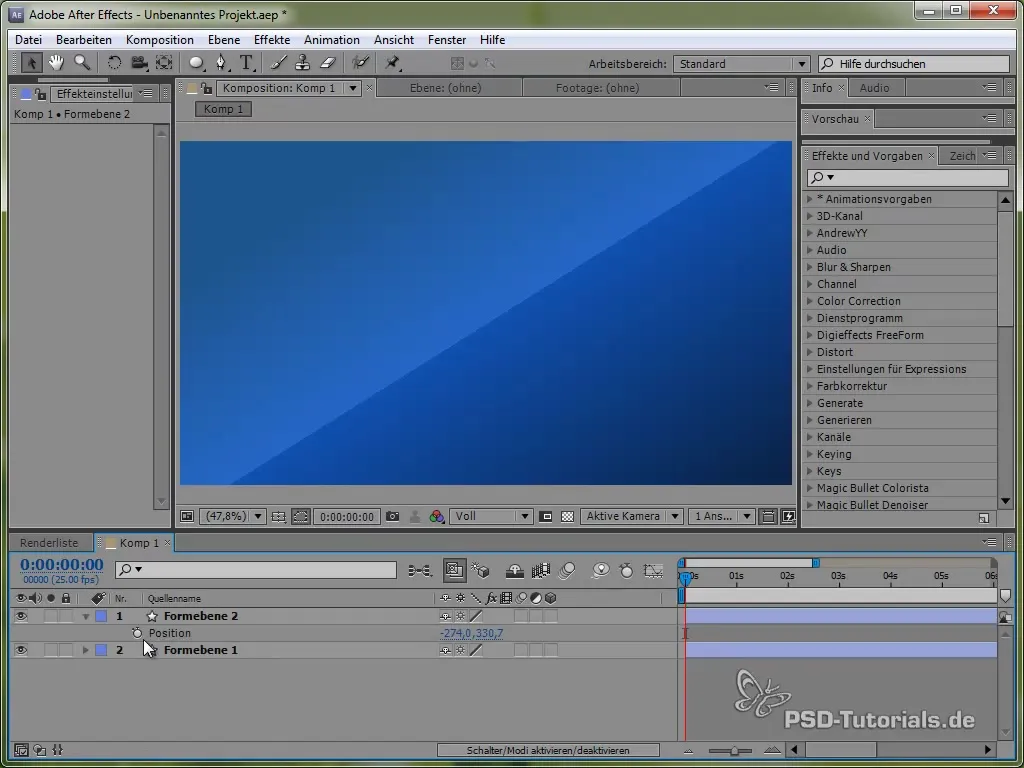
Hierfür verwenden wir zuerst die Zeitvariable time, multipliziert mit einem Wert, der die Geschwindigkeit der Bewegung festlegt. Zum Beispiel:

value[0] + time * 150

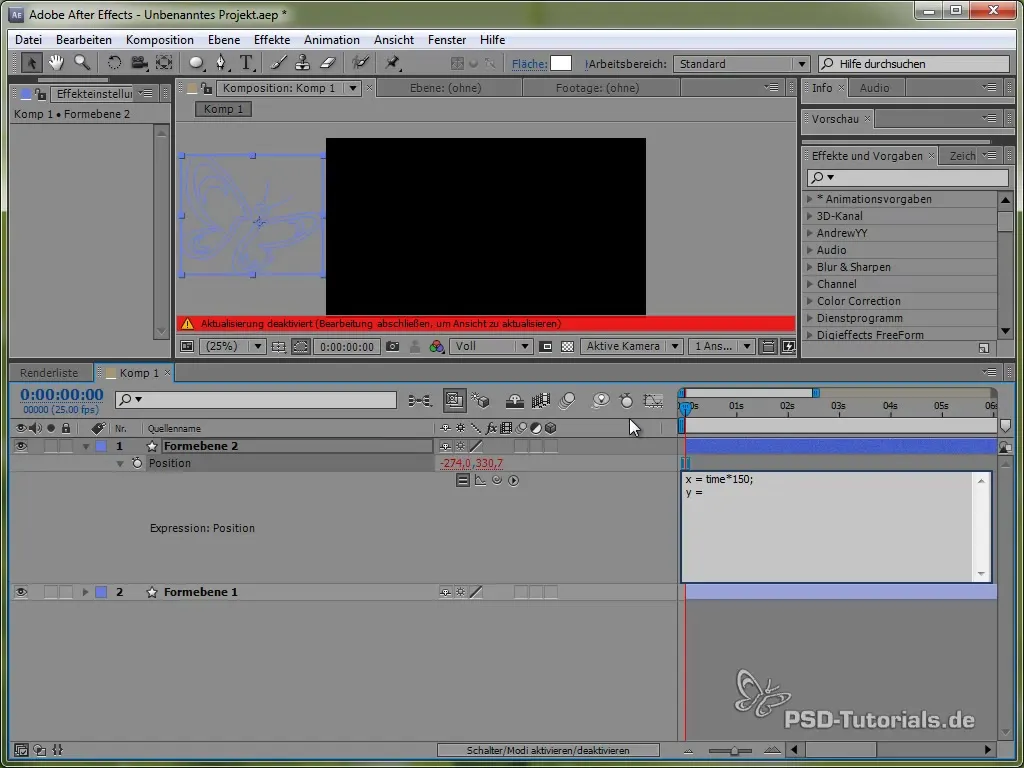
Dieser Code bewirkt, dass der Schmetterling in der X-Richtung konstant um 150 Pixel pro Sekunde bewegt wird. Für die Y-Richtung werden wir eine Sinusfunktion verwenden, die die vertikale Bewegung des Schmetterlings erzeugt und diesen zwischen bestimmten Werten „schwanken“ lässt.

Anwendung der Sinusfunktion

Die Y-Bewegung wird durch folgende Expression definiert:

value[1] + 40 * Math.sin(2 * Math.PI * time)

Hierbei setzt Math.sin() die Sinusfunktion um. Sie variiert zwischen -1 und 1 und wird mit 40 multipliziert, was bedeutet, dass der Schmetterling in der Y-Richtung zwischen -40 und 40 Pixeln schwankt.

Bewegungsgraphik visualisieren

Um diese Bewegung besser zu visualisieren, kannst du das Graphenfenster in After Effects aktivieren. Dies zeigt dir die Schwankungen des Sinuswertes klarer.

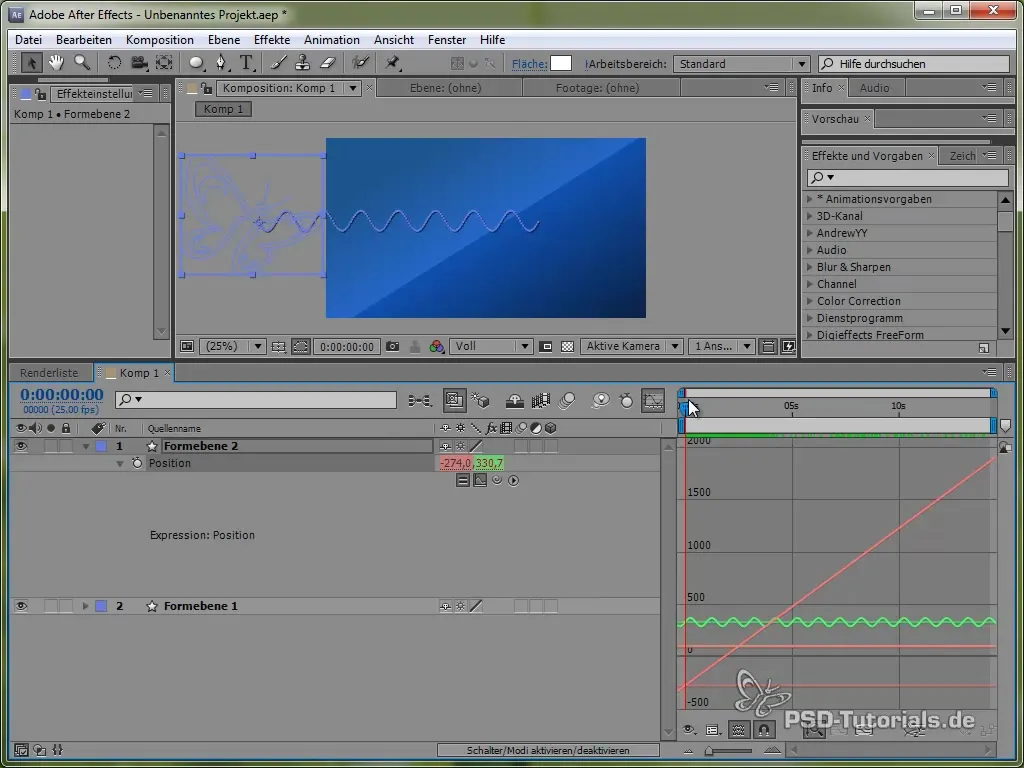
Man sieht, dass das Signal oszilliert und sich über den Bildschirm bewegt.

Amplitude und Frequenz variieren

Jetzt kannst du die Amplitude anpassen, um unterschiedlich starke Schwankungen zu erzeugen. Wenn du zum Beispiel die Amplitude per Zeit erhöhen möchtest, könntest du Folgendes nutzen:

40 * (time * 10) * Math.sin(2 * Math.PI * time)

Damit wird die Amplitude mit der Zeit steigen, was bewirkt, dass der Schmetterling nach einer Sekunde um 40 Pixel schwankt, nach zwei Sekunden um 80 Pixel und so weiter.

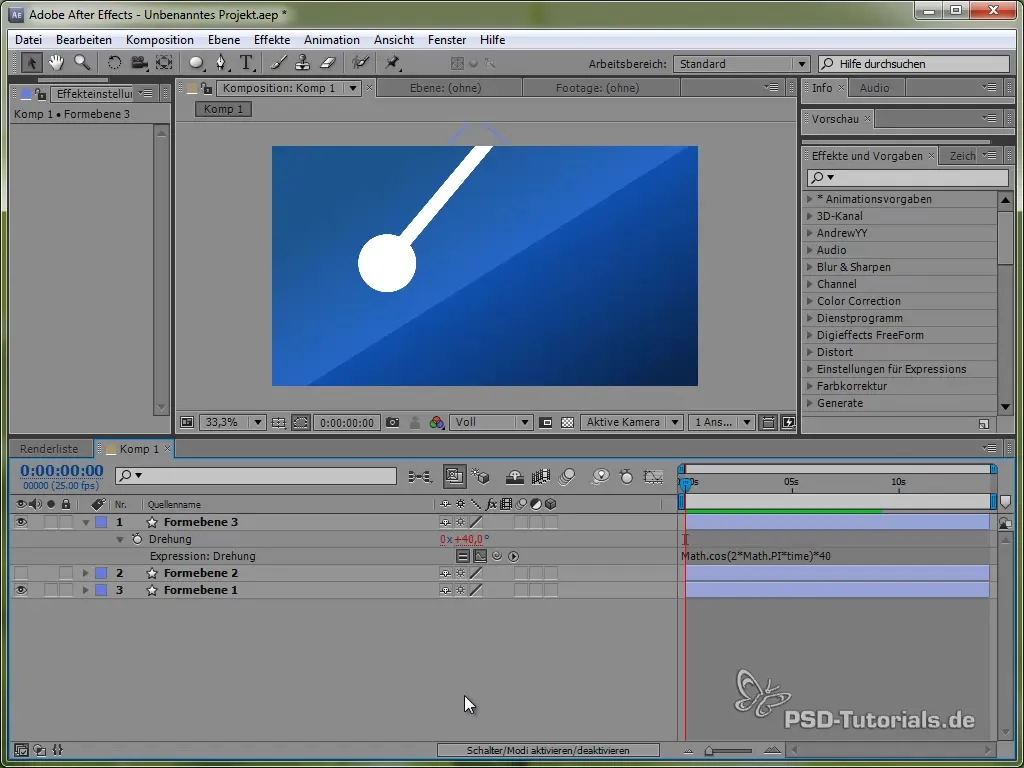
Pendel erstellen

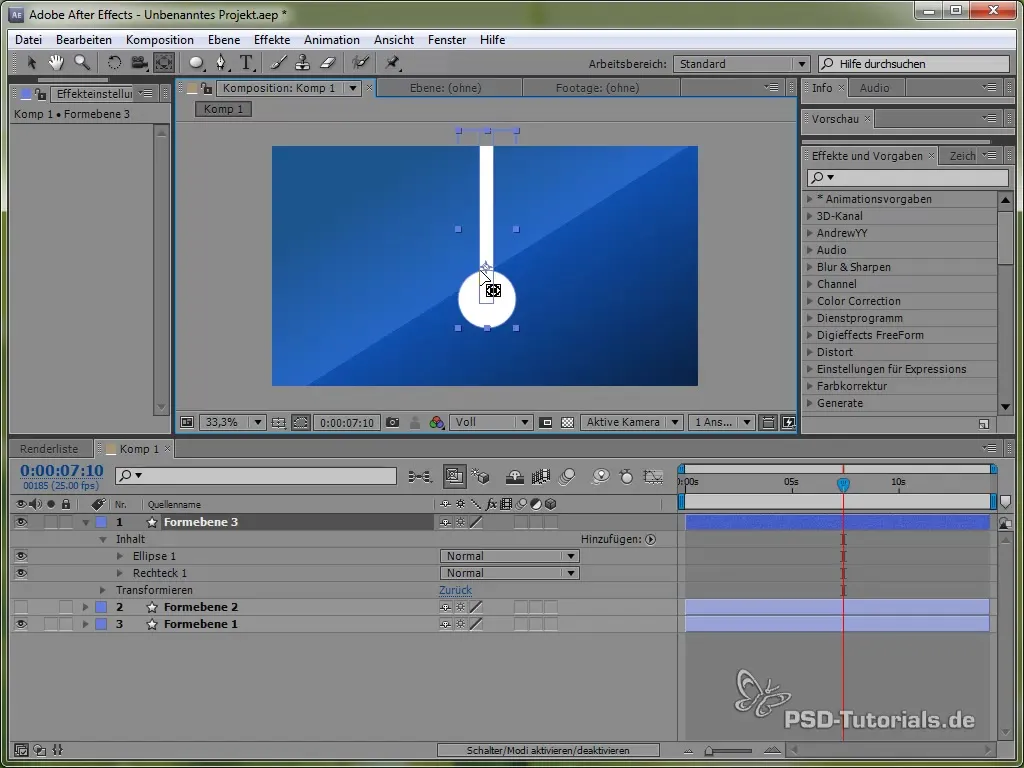
Um den Umgang mit verschiedenen physikalischen Simulationen zu vertiefen, wenden wir uns nun der Erstellung eines Pendels zu. Zeichne zuerst einen dünnen Stab und füge eine Ellipse an dessen Ende hinzu.

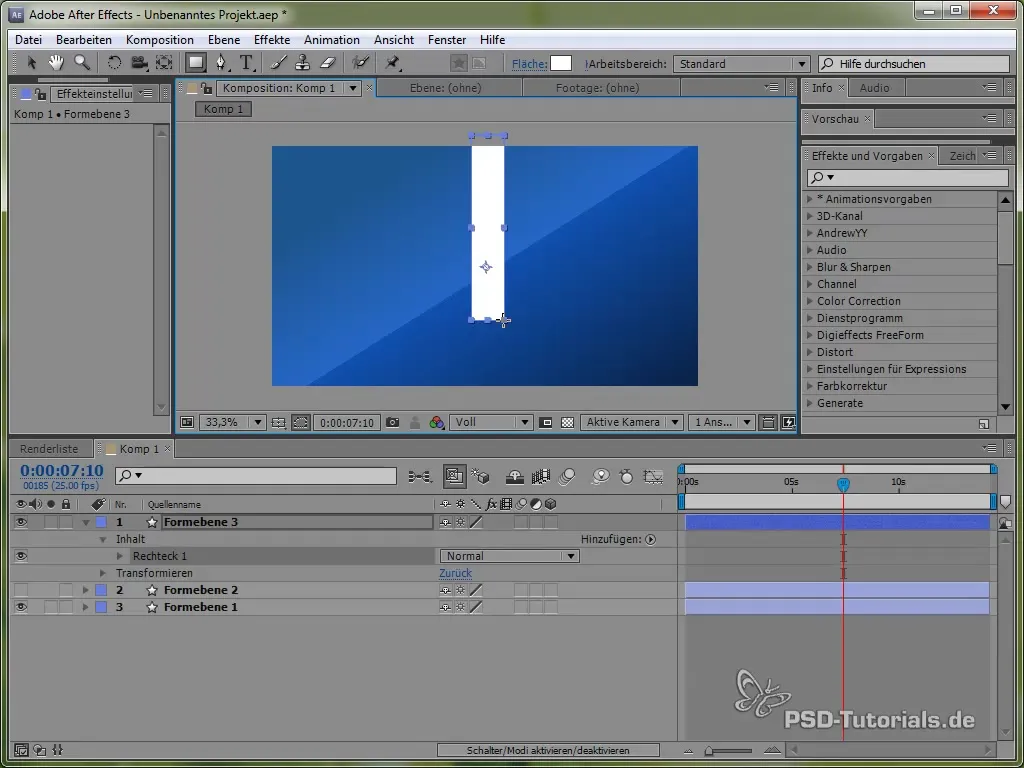
Positioniere den Ankerpunkt oben vom Pendel, sodass es schwingen kann. Dies geschieht mit dem Werkzeug für den Ankerpunkt.

Setze dann die Expression:

value + 40 * Math.cos(2 * Math.PI * time)

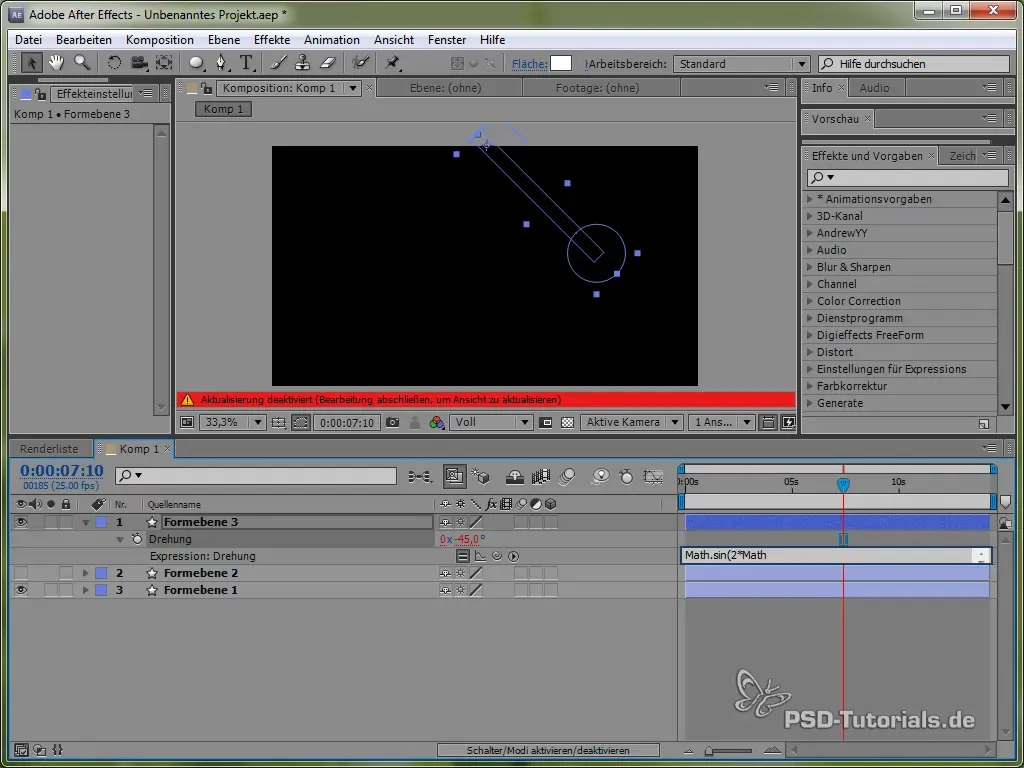
Durch den Cosinus starten wir den Schwingungsprozess von einem positiven Punkt, was realistisch ist, da das Pendel oben anfängt, zu schwingen.

Dämpfungseffekte einfügen

Um Dämpfung in die Schwingung zu integrieren, verwenden wir die exponentielle Funktion. Dadurch wirkt die Schwingung realistischer, da sie anfangs stark ist und schließlich abnimmt.

Ein Beispiel-Code könnte so aussehen:

40 * Math.cos(2 * Math.PI * time) / Math.exp(time)

Hierbei sorgt die Division durch die Exponentialfunktion für eine langsame Dämpfung.

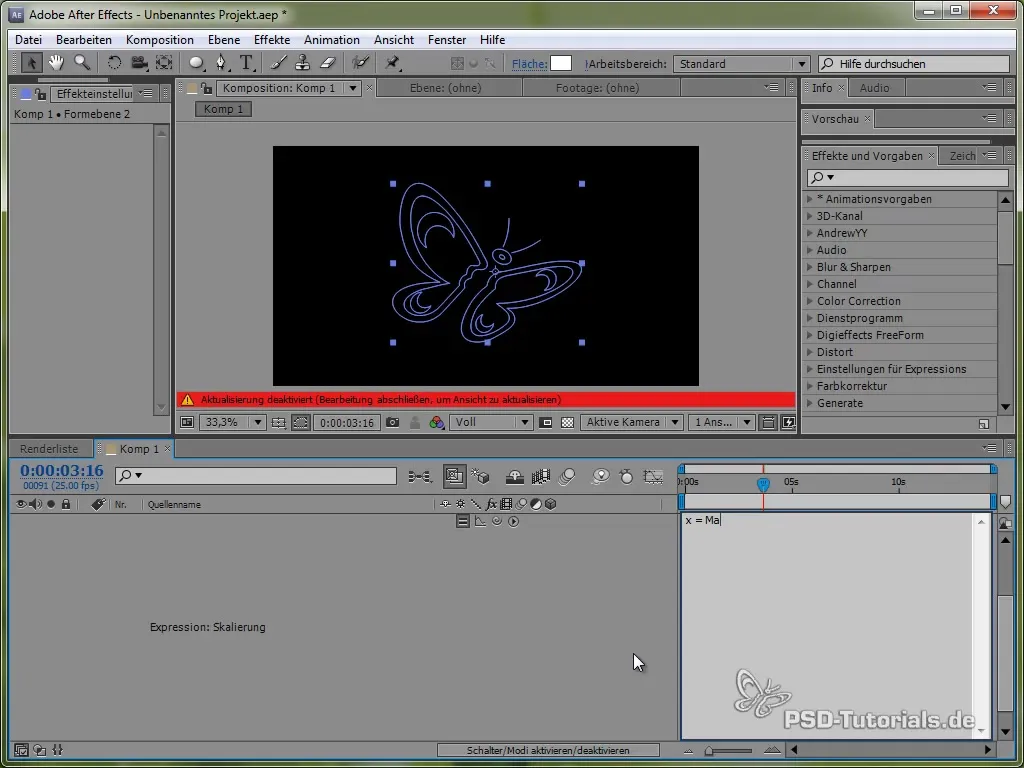
Squash und Stretch hinzufügen

Für lebendigere Animationen kannst du auch den Squash and Stretch-Effekt hinzufügen. Das kannst du über die Skalierung des Schmetterlings erreichen.

Du tust dies, indem du eine Expression auf die Skalierungsskala anwendest, die sowohl auf x- als auch auf y-Werte angewendet werden kann, wobei du eine Sinus- oder Cosinus-Funktion benutzt.

Finale Gedanken

Man sieht, dass durch die richtige Anwendung von trigonometrischen und exponentiellen Funktionen sehr realistische und interessante Animationen geschaffen werden können. Du hast gelernt, wie man einen Schmetterling fliegen lässt, ein Pendel schwingeln lässt und wie man mit Effekten wie Squash and Stretch arbeitet.

Zusammenfassung - Mathe in Expressions: Trigonometrische & Exponentielle Funktionen

Mathematik im Kontext von Expressions in After Effects eröffnet dir die Möglichkeit, kreative und lebendige Animationen zu erstellen. Trigonometrische und exponentielle Funktionen sind dabei essenziell. In diesem Tutorial hast du Erfahrungen mit der Nutzung dieser mathematischen Konzepte in der Praxis gemacht.