Math in Expressions: Trigonometric & Exponential Concepts

Mathematics plays a fundamental role in the digital world, and especially in video editing with After Effects (AE), it opens up entirely new possibilities for you. In this tutorial, you will learn how to use trigonometric and exponential functions in AE as Expressions to create fascinating animations. A particularly exciting example will be the movement of a butterfly, demonstrating how physical simulations can be implemented using mathematics.

Key Insights

• Trigonometric functions such as sine and cosine can be used to create offset movements.
• Exponential functions are used to simulate damping effects.
• The use of absolute values in functions can help achieve certain animation effects.

Step-by-Step Guide

Animating the Butterfly

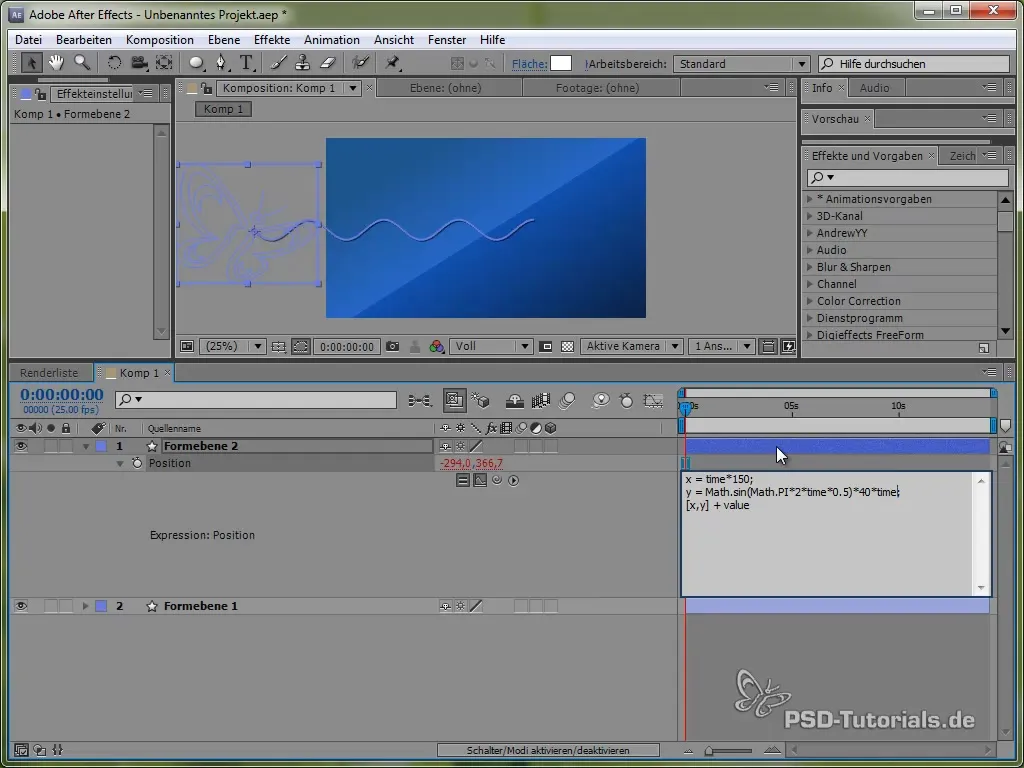
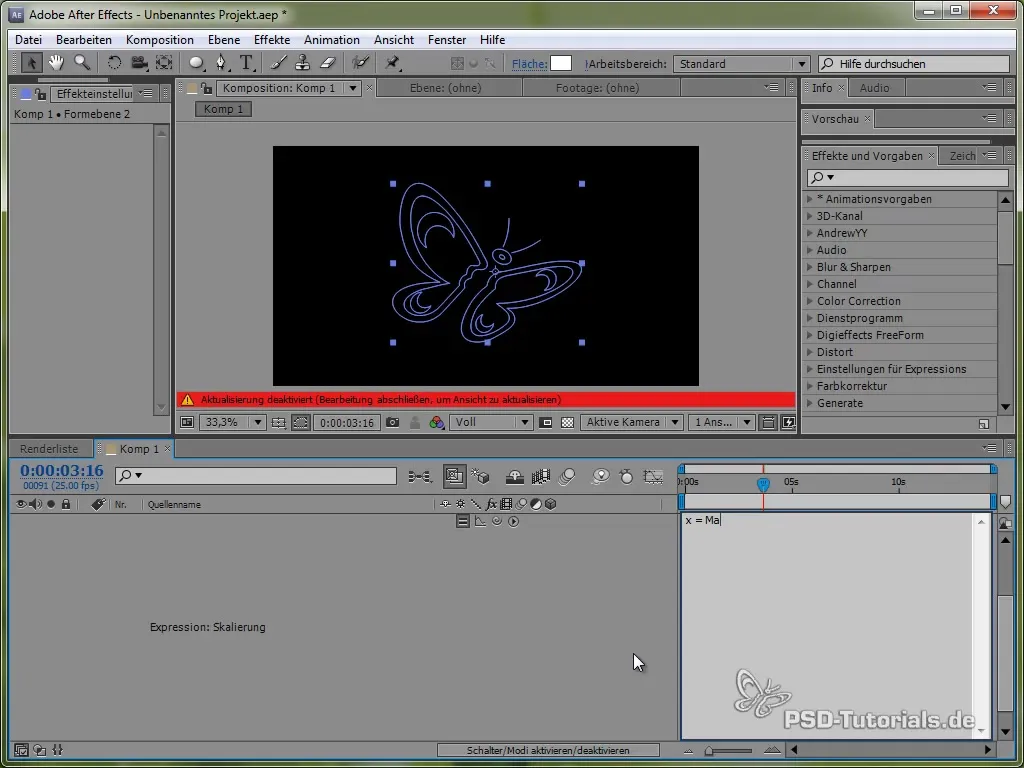
To move our butterfly, you first need to animate it so that it moves in a wave. This wave motion can be easily achieved with expressions.

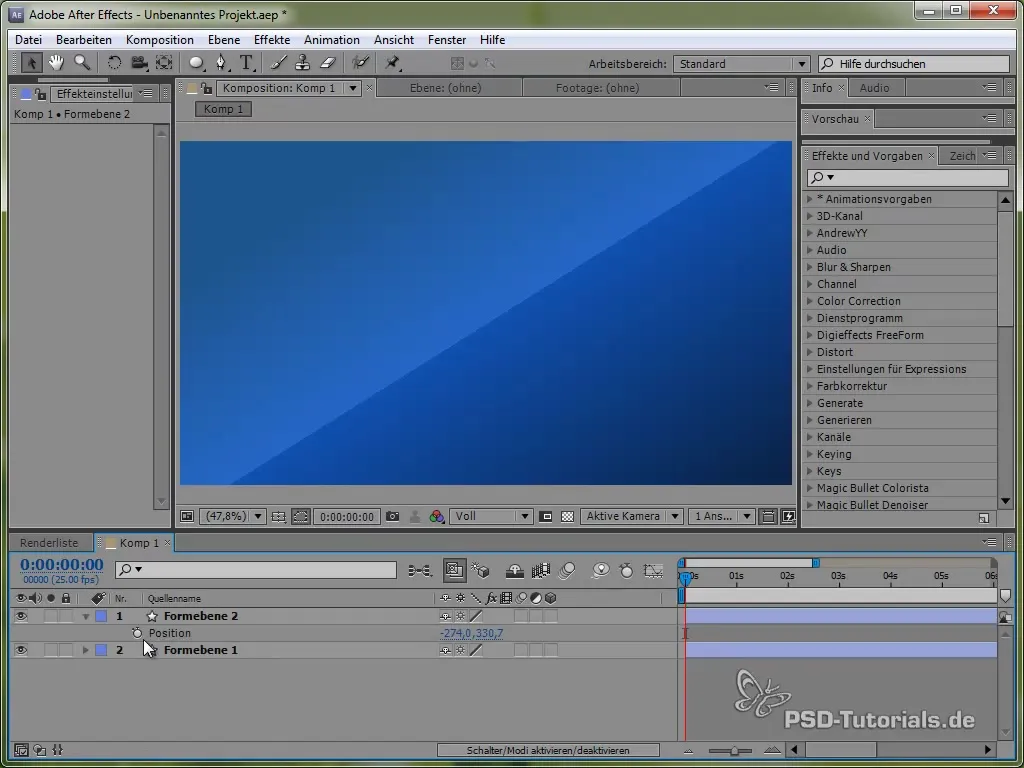
Start by opening the butterfly's position by pressing the "P" key. Then set an expression for the position by holding down the ALT key and clicking on the stopwatch.

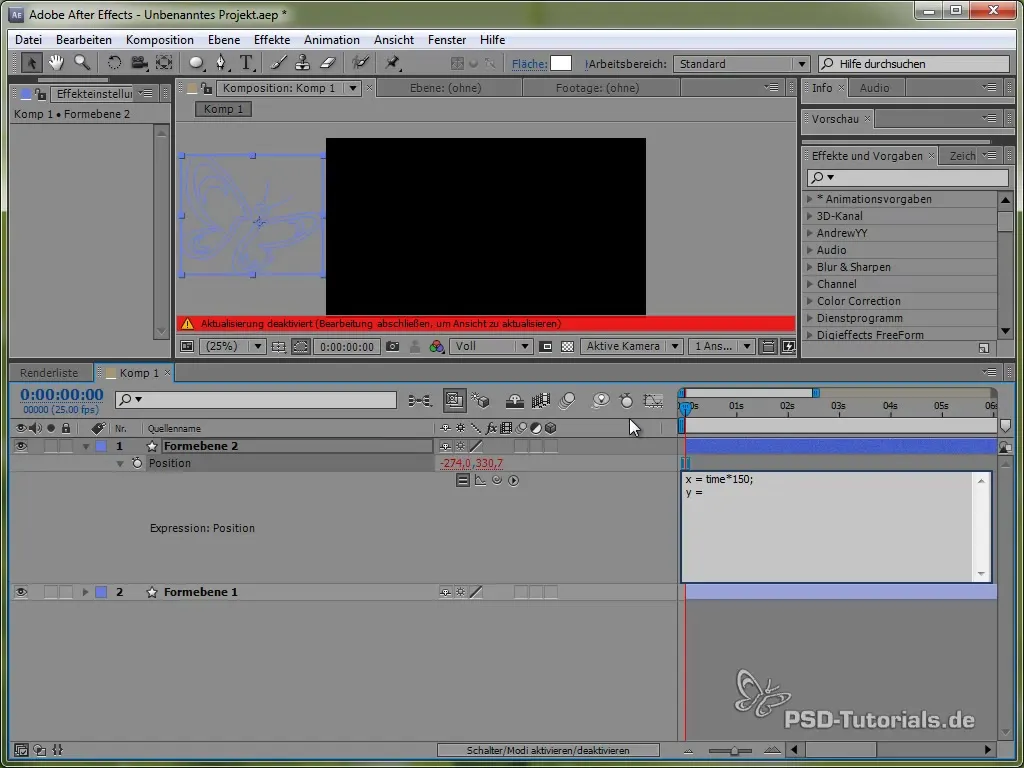
For this, we first use the time variable time, multiplied by a value that determines the speed of the movement. For example:

value[0] + time * 150

This code causes the butterfly to move constantly 150 pixels per second in the X direction. For the Y direction, we will use a sine function, which generates the vertical movement of the butterfly and makes it "swing" between specific values.

Applying the Sine Function

The Y movement is defined by the following expression:

value[1] + 40 * Math.sin(2 * Math.PI * time)

Here, Math.sin() implements the sine function. It varies between -1 and 1 and is multiplied by 40, which means that the butterfly swings in the Y direction between -40 and 40 pixels.

Visualizing the Motion Graph

To better visualize this movement, you can activate the graph window in After Effects. This will clarify the fluctuations of the sine value.

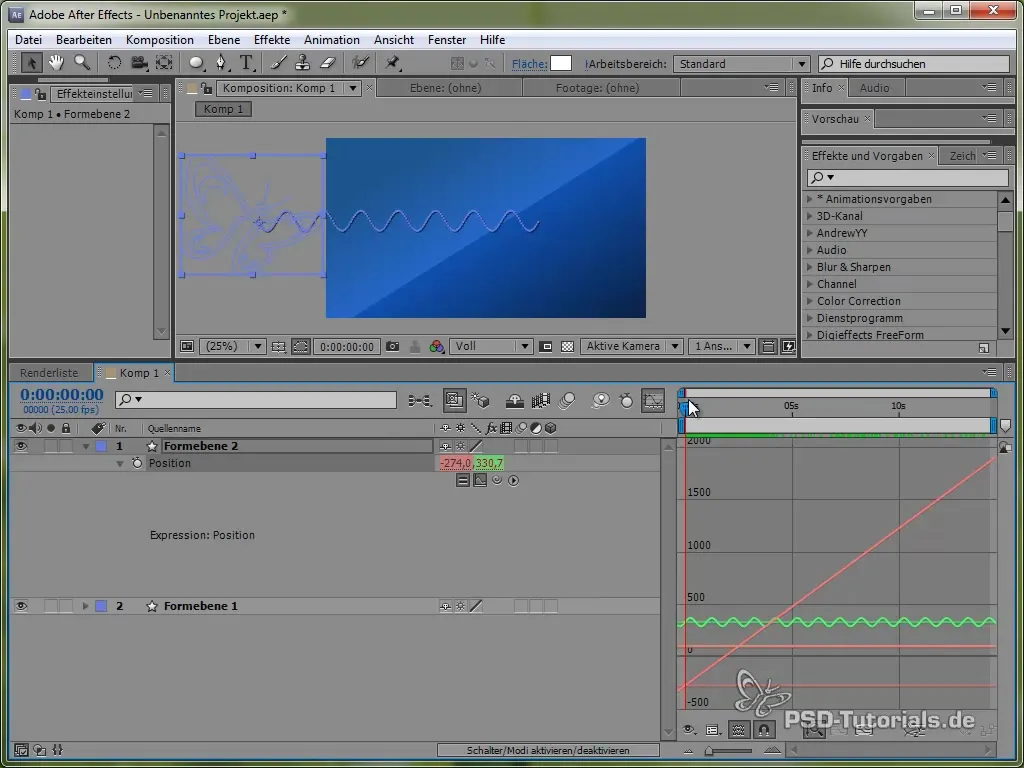
You can see that the signal oscillates and moves across the screen.

Varying Amplitude and Frequency

Now you can adjust the amplitude to create different levels of swinging. For example, if you want to increase the amplitude over time, you could use the following:

40 * (time * 10) * Math.sin(2 * Math.PI * time)

This will cause the amplitude to increase over time, resulting in the butterfly swinging 40 pixels after one second, 80 pixels after two seconds, and so on.

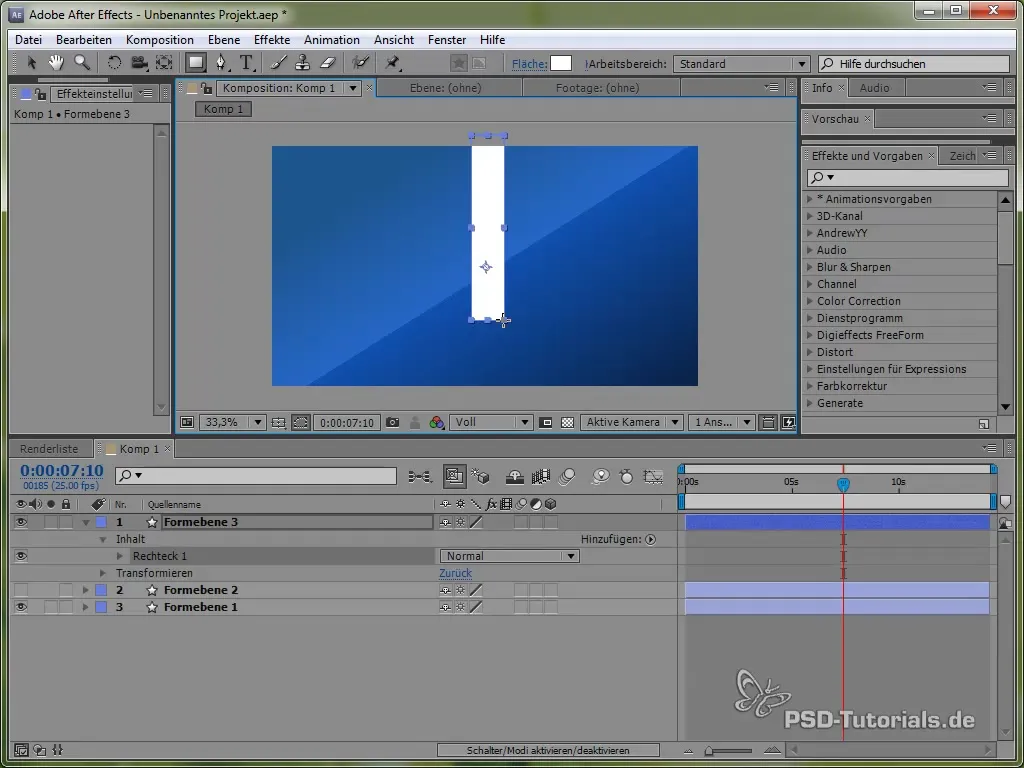
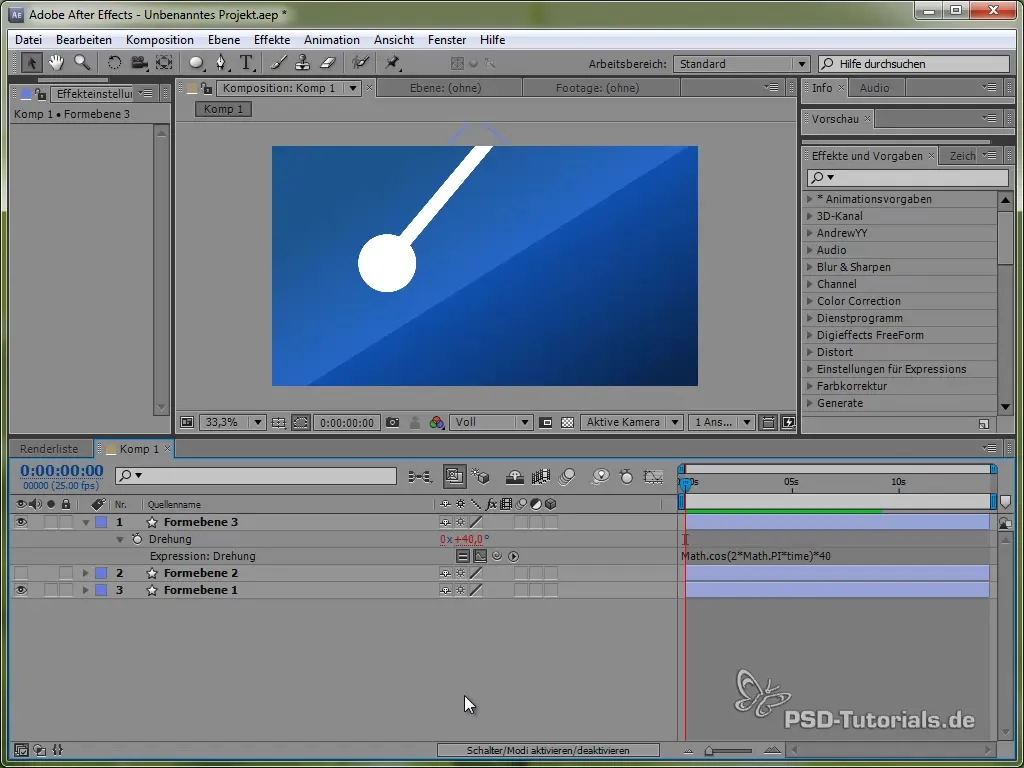
Creating a Pendulum

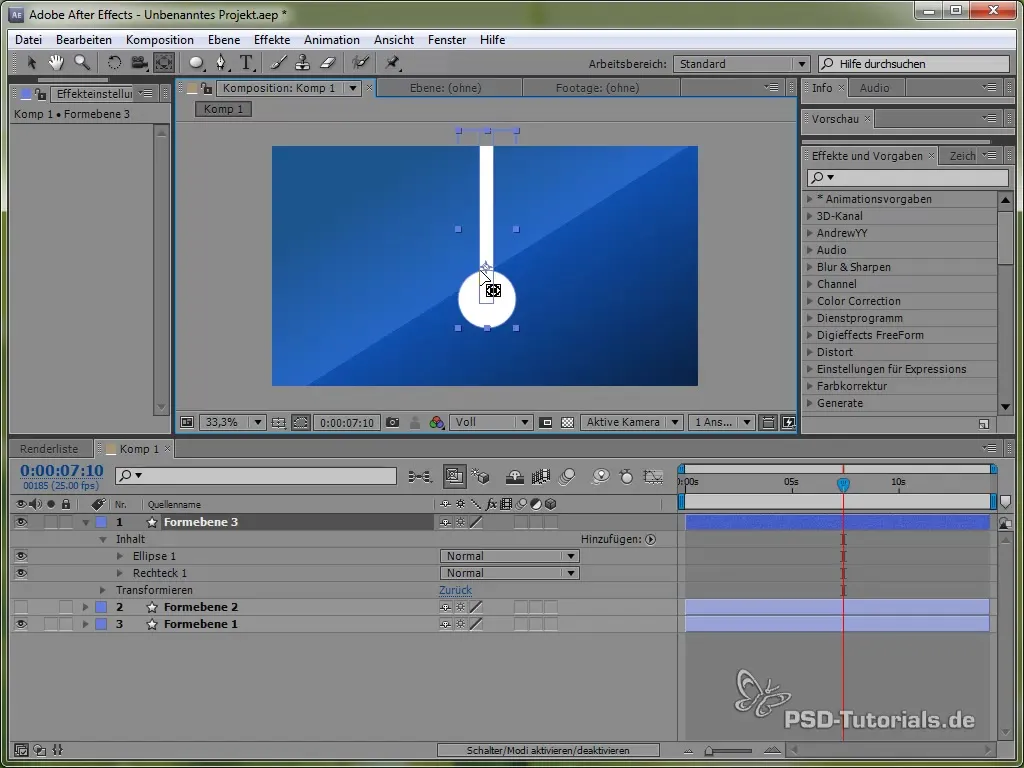
To deepen your understanding of various physical simulations, we will now create a pendulum. First, draw a thin rod and add an ellipse at its end.

Position the anchor point at the top of the pendulum so it can swing. You can do this with the anchor point tool.

Then set the expression:

value + 40 * Math.cos(2 * Math.PI * time)

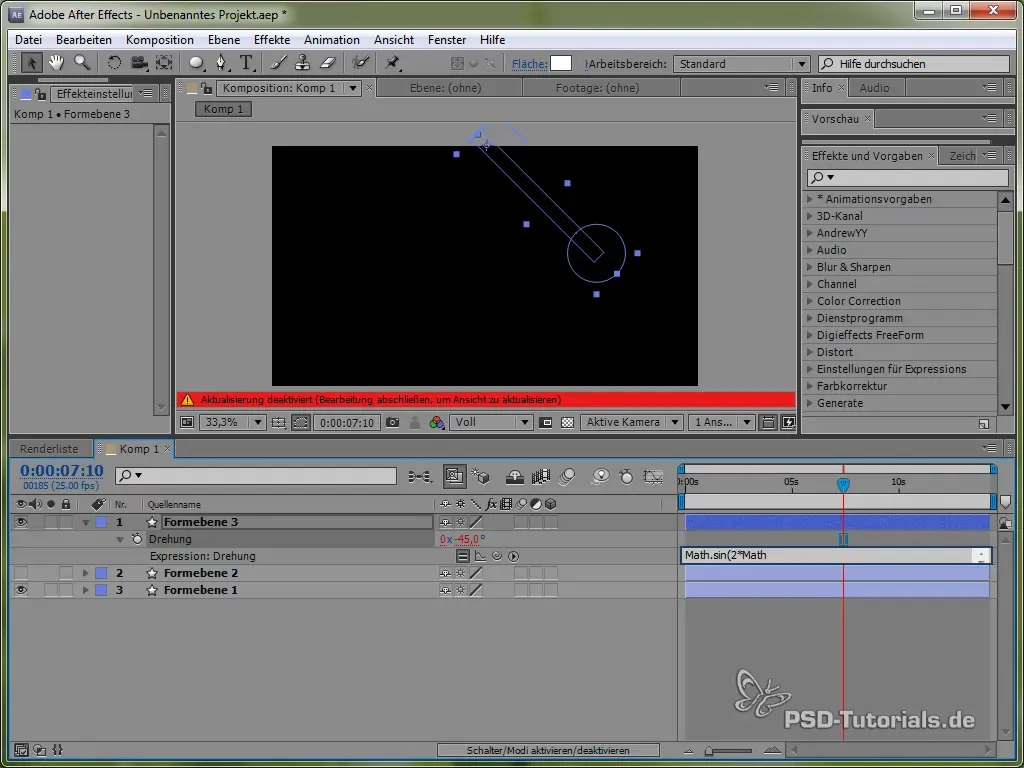
By using cosine, we start the oscillation process from a positive point, which is realistic because the pendulum begins to swing from the top.

Incorporating Damping Effects

To integrate damping into the swing, we use the exponential function. This makes the swing more realistic, as it starts strong and then gradually decreases.

An example code could look like this:

40 * Math.cos(2 * Math.PI * time) / Math.exp(time)

Here, the division by the exponential function causes a slow damping effect.

Adding Squash and Stretch

For livelier animations, you can also add the squash and stretch effect. You can achieve this through the scaling of the butterfly.

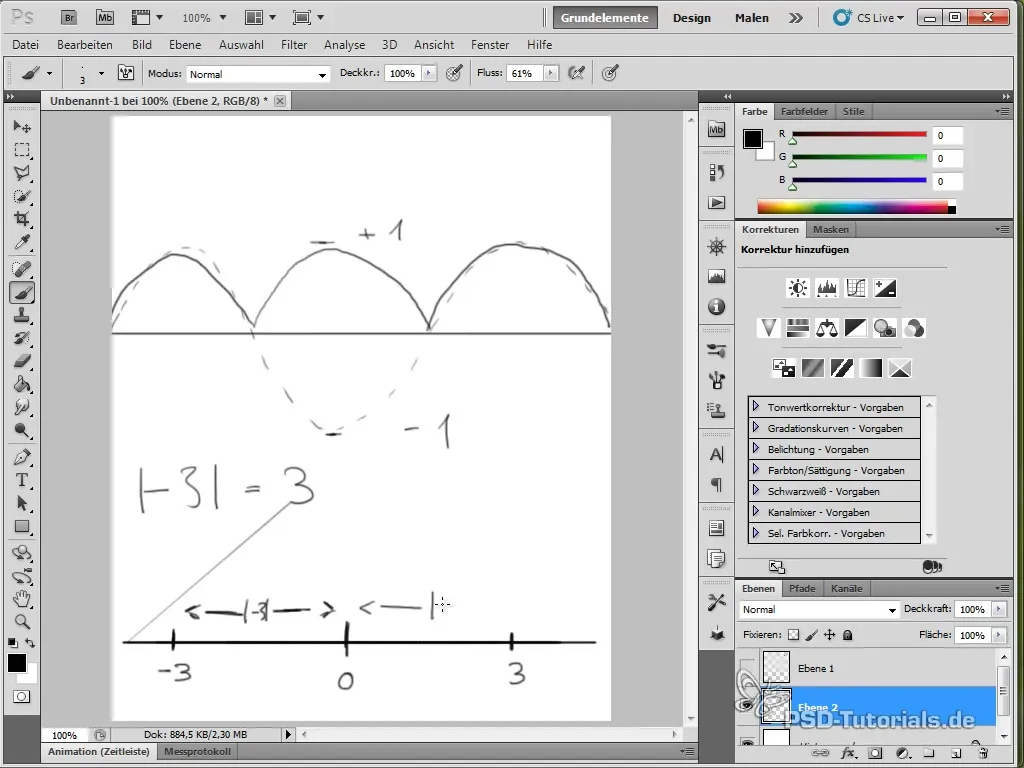
You do this by applying an expression to the scale property, which can be applied to both x and y values, using a sine or cosine function.

Final Thoughts

It is clear that through the correct application of trigonometric and exponential functions, very realistic and interesting animations can be created. You have learned how to make a butterfly fly, how to make a pendulum swing, and how to work with effects like squash and stretch.

Summary - Math in Expressions: Trigonometric & Exponential Functions

Mathematics in the context of expressions in After Effects gives you the opportunity to create creative and lively animations. Trigonometric and exponential functions are essential in this process. In this tutorial, you have gained experience in applying these mathematical concepts in practice.